1、數據表示的作用

（1）定義：將數據按照某種方式組織，以便機器硬件能直接識別和使用。現代計算機采用二進制進行數據表示。

（2）數據表示考慮因素：

• 數據的類型： 數值/非數值、小數、整數、英文字符、漢字
• 表示的范圍和精度：滿足日常計算需要
• 存儲和處理的代價：硬件開銷，處理性能
• 軟件的可移植性：方便在不同機器之間移植

（3）進制轉化：

• 二進制轉十進制——按權相加法，小數點前2的次方從0 開始，小數點后2的次方從-1開始
• 十進制轉二進制——整數部分除基取余法，小數部分乘基取余法
• 二進制、八進制、十六進制：一位八進制對應三位二進制，一位十六進制對應四位二進制

2、數值數據表示?

機器數 （解決符號問題）

（1）真值 (書寫格式) ：將用“+”、“-” 表示正負的二進制數稱為真值

（但是機器是識別不來書寫格式的，那么在計算機中我們該怎么表示負數？這里就需要引入機器碼的概念了）

---

（2）機器碼 ? (機器內部使用)：將符號和數值一起編碼表示的二進制數稱為機器碼

所謂原碼，就是二進制的最高位為符號位，1表示負數，0表示正數，其他位為數值位保持不變。

[+89]原 ? ?= 01011001 ? ? ?[-77]原 ? ?= 11001101 ? ?[-0.75]原 = 1.11 ?

所謂反碼，如果是正數，則表示方法和原碼一樣；如果是負數，符號位不變，其余各位取反。

[+89]原 ? ?= ?01011001 ? ? [+89]反 ? ?= ?01011001 [-77]原 ? ? = ?11001101? ? ?[-77]反 ? ? = ?10110010 ? [-0.75]原 = ?1.11? ? ? ? ? ? ? ?[-0.75]反 = ?1.00 ?

補碼

正值——直接取其原來的二進制碼，符號位為0

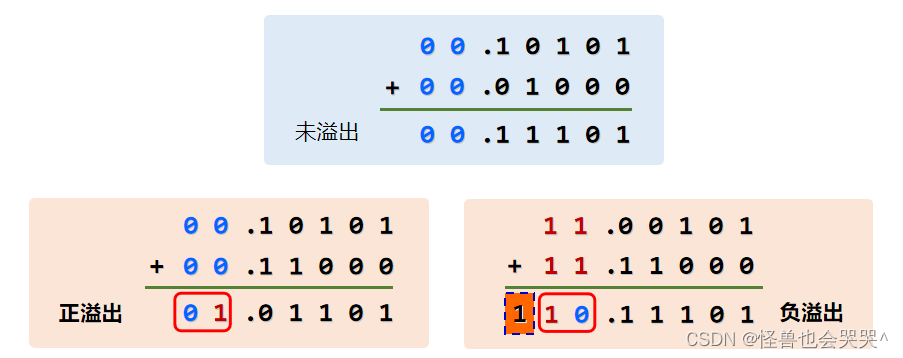
負值——有三種求法 反碼法 逐位取反，末位加1，符號位為1? [-10101010]補 = 1 01010101+1 = 1 01010110 ? [-0.010101]補 = ?1.101011 掃描法 從最右側開掃描找到第一個1，該數位左側所有數據位取反，其他數據位不變 模運算 模：符號位進位位的權值

雙符號位補碼——符號位01表示正溢出，10表示負溢出，最高位表示正確符號位 雙符號位最高位永遠是正確符號位

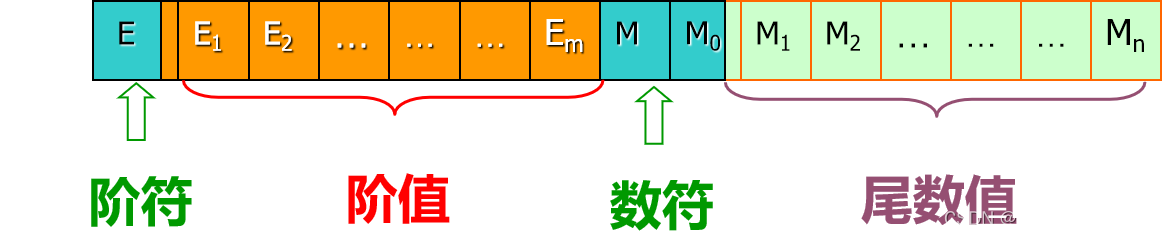
移碼僅用于表示整數，通常表示浮點數的階碼。 移碼=真值+偏移量? ? ?[x]移 = 2n+x ? ? -2n ≤ x < 2n

與補碼的符號位相異，數據位相同 零有唯一的表示方式[＋0000000]移= [-0000000]移= 10000000 符號位參與運算

將十進制真值(－127,－1,0,＋1,＋127)列表表示成二進制數及原碼、反碼、補碼、移碼值（機器字長8位，偏移量128）。

| 真值D  | 真值B        | [x]原     | [x]反     | [x]補     | [x]移      |
|--------|--------------|-----------|-----------|-----------|-----------|
| -127   | -01111111    | 11111111  | 10000000  | 10000001  | 00000001  |
| -1     | -00000001    | 10000001  | 11111110  | 11111111  | 01111111  |
| 0      |  00000000    | 10000000  | 11111111  | 00000000  | 10000000  |
| +1     | +01111111    | 00000001  | 00000001  | 00000001  | 10000001  |
| +127   | +01111111    | 01111111  | 01111111  | 01111111  | 11111111  |

定點表示 ?（小數點位置固定的數)

定點數表示數的范圍受字長限制，表示數的范圍有限 定點表示的精度有限

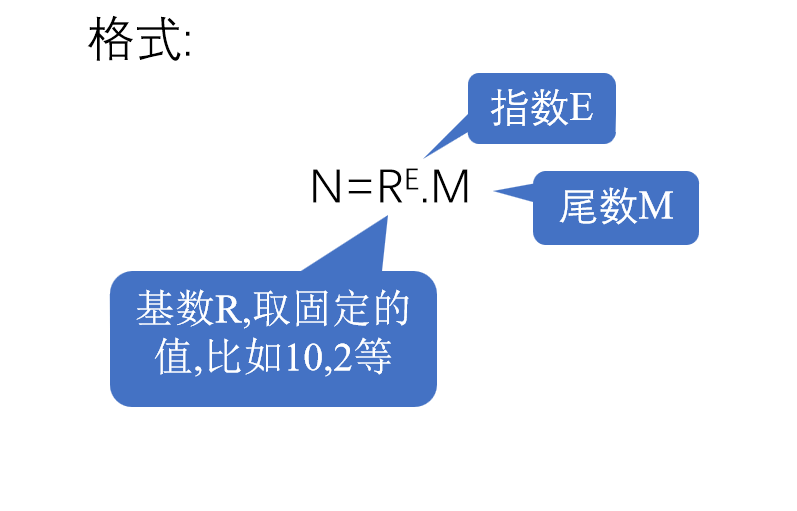
浮點表示（小數點位置隨階碼不同而浮動）

機器字長一定時，階碼越長，表示范圍越大

浮點數表示范圍比定點數大，精度高?

?

3、?非數值數據表示法