操作環境:
MATLAB 2022a
1、算法描述
極化碼(Polar Code)
極化碼(Polar Code)是一種新型的信道編碼技術,由土耳其裔教授Erdal Ar?kan在2008年提出。極化碼在理論上被證明能夠在信道容量上達到香農極限,因此引起了廣泛的關注和研究。極化碼的核心思想是通過極化變換將原本均勻的信道轉換為完全可靠和完全不可靠的兩類,從而實現高效的信息傳輸。
極化碼的基本原理
極化碼的編碼過程基于一個稱為極化變換(channel polarization)的現象。具體來說,極化變換利用了一種特定的線性變換,將多個獨立且等價的二進制離散記憶信道(B-DMC)轉化為新的信道,這些新信道中的一些變得完全可靠,而另一些則變得完全不可靠。
在n次編碼中,極化碼將n個原始信道極化為2^n個信道,其中部分信道變得接近完全可靠(即誤碼率接近零),其余信道則變得接近完全不可靠(即誤碼率接近0.5)。通過選取這些完全可靠的信道傳輸信息比特,而將完全不可靠的信道用于傳輸固定的凍結比特(預設值,通常為0),極化碼實現了高效的編碼。
極化碼的編碼和解碼過程主要包括以下幾個步驟:
- 極化變換:應用一系列傅立葉變換和反傅立葉變換,對原始信道進行極化。
- 凍結比特選擇:根據極化后的信道可靠性,選擇信息比特和凍結比特的位置。
- 編碼:將信息比特和凍結比特按選定的位置排列,進行極化編碼。
- 解碼:通過極化譯碼算法,從接收到的信號中恢復原始信息。
極化碼的編碼過程
極化碼的編碼過程可以通過一個簡單的例子來說明。設定一個長度為N的碼字,其中N=2^n。首先,定義一個基礎的極化矩陣F:

對于任意N=2^n,極化矩陣可以通過Kronecker積(Kronecker product)遞歸計算得到:

通過極化矩陣F的遞歸構造,可以得到所需的極化矩陣GN。
例如,當N=4時,極化矩陣為:

編碼過程通過將信息比特和凍結比特按指定位置排列,并與極化矩陣相乘來完成。
極化碼的解碼算法
極化碼的解碼主要有以下五種常見方法:SC、SCL、SSC、SCAN和BP解碼。每種方法都有其獨特的優點和適用場景。
1. 逐次消除(SC)解碼
逐次消除(Successive Cancellation, SC)解碼是極化碼的基本解碼算法。它按照比特的順序逐個進行解碼,每解碼一個比特就利用已解碼的比特信息來幫助解碼下一個比特。
SC解碼的基本步驟如下:
- 初始化:根據接收到的碼字和極化矩陣計算初始的對數似然比(LLR)。
- 逐次解碼:按照比特順序進行逐次消除解碼,每次解碼一個比特,并根據之前解碼的結果更新LLR值。
- 判決:對每個比特進行硬判決(即判斷是0還是1)。
SC解碼的優點是實現簡單,計算復雜度較低(為O(N log N))。但其缺點是性能相對較差,尤其是在高噪聲環境下。
2. 逐次消除列表(SCL)解碼
逐次消除列表(Successive Cancellation List, SCL)解碼是在SC解碼的基礎上引入了列表跟蹤機制,以提高解碼性能。在SCL解碼中,保持多個候選路徑(即候選的比特序列),并在每一步選擇若干最有可能的路徑繼續解碼。
SCL解碼的基本步驟如下:
- 初始化:根據接收到的碼字和極化矩陣計算初始的LLR。
- 逐次解碼:按照比特順序進行逐次消除解碼,并在每次解碼時保留若干候選路徑。
- 路徑選擇:在每個解碼步驟中,選擇若干最有可能的路徑,并丟棄其他路徑。
- 最終判決:在解碼結束時,根據路徑的概率或度量選擇最優路徑。
SCL解碼顯著提高了解碼性能,尤其是在選擇較大列表長度(L)時。其計算復雜度為O(LN log N)。
3. 簡化逐次消除(SSC)解碼
簡化逐次消除(Simplified Successive Cancellation, SSC)解碼是一種優化的SC解碼方法,利用了極化碼結構中的冗余性,以減少解碼復雜度。SSC解碼通過識別特殊的碼塊結構,直接對這些結構進行快速解碼。
SSC解碼的基本步驟如下:
- 初始化:根據接收到的碼字和極化矩陣計算初始的LLR。
- 識別特殊結構:在逐次消除解碼過程中,識別極化碼中的特殊結構(如全零塊、全一塊等)。
- 快速解碼:對于識別出的特殊結構,直接應用預定義的解碼規則進行快速解碼。
- 逐次解碼:對于非特殊結構,繼續進行逐次消除解碼。
SSC解碼在減少復雜度的同時,保持了SC解碼的性能,其計算復雜度一般為O(N log N)。
4. SCAN解碼
SCAN解碼是一種迭代解碼方法,類似于LDPC碼的消息傳遞算法。SCAN解碼通過多次迭代在比特節點之間傳遞消息,以提高解碼性能。
SCAN解碼的基本步驟如下:
- 初始化:根據接收到的碼字和極化矩陣計算初始的LLR。
- 迭代消息傳遞:在比特節點之間傳遞消息,更新LLR值。每次迭代包括從左向右和從右向左兩個方向的消息傳遞。
- 判決:在迭代結束后,對每個比特進行硬判決。
SCAN解碼的計算復雜度取決于迭代次數和消息傳遞的復雜度,通常為O(N log N)到O(N^2)之間。
5. 置信傳播(BP)解碼
置信傳播(Belief Propagation, BP)解碼是一種基于圖模型的迭代解碼方法,適用于極化碼的高效解碼。BP解碼通過在極化碼的因子圖上進行消息傳遞,以估計每個比特的后驗概率。
BP解碼的基本步驟如下:
- 初始化:根據接收到的碼字和極化矩陣構建初始的因子圖,并計算初始的LLR。
- 迭代消息傳遞:在因子圖的節點之間傳遞消息,更新每個比特的后驗概率。
- 判決:在迭代結束后,根據后驗概率對每個比特進行硬判決。
BP解碼的性能通常優于SC和SCL解碼,但其計算復雜度較高,通常為O(N log N)到O(N^2)之間。
2、仿真結果演示

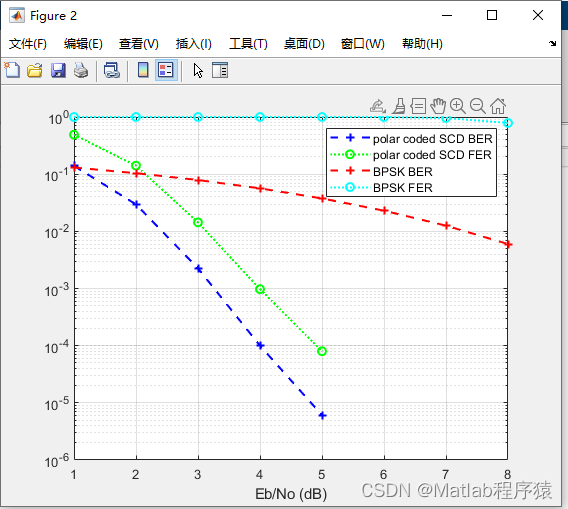

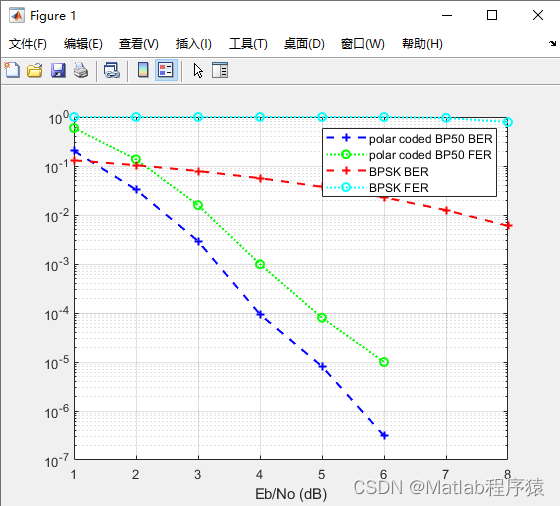

3、關鍵代碼展示
略
4、MATLAB?源碼獲取
? V
點擊下方名片關注公眾號獲取









)

)


)




的方式)