K-Means 是一種常用的無監督學習算法，廣泛應用于數據聚類分析。本文將詳細講解 K-Means 算法的原理、步驟、公式以及 Python 實現，幫助你深入理解這一經典算法。

什么是 K-Means 算法？

K-Means 算法是一種基于原型的聚類算法，其目標是將數據集分成K個簇（clusters），使得同一簇內的數據點盡可能相似，不同簇之間的數據點盡可能不同。每個簇由其中心（即質心，centroid）表示。

K-Means 算法的步驟

K-Means 算法的主要步驟如下：

1. 初始化：隨機選擇 K個數據點作為初始質心。
2. 分配簇：將每個數據點分配到距離其最近的質心對應的簇。
3. 更新質心：計算每個簇的質心，即簇內所有數據點的平均值。
4. 重復步驟 2 和 3：直到質心不再發生變化（或變化很小），或者達到預設的迭代次數。

詳細步驟解釋

1. 初始化：

   • 從數據集中隨機選擇K 個點作為初始質心。這些質心可以是數據集中的實際點，也可以是隨機生成的點。

2. 分配簇：

   • 計算每個數據點到所有質心的距離（通常使用歐氏距離）。對于數據點 $(x_i)$ 和質心$({\mu }_j)$，歐氏距離計算公式為：
     $$d(x_i,{\mu }_j)=\sqrt{\sum _{m=1}^M(x_{im}?{\mu }_{jm}{)}^2}$$
   • 將每個數據點分配到距離其最近的質心對應的簇，即：
     C i = { x p : ∥ x p ? μ i ∥ ≤ ∥ x p ? μ j ∥ , ? j , 1 ≤ j ≤ k } \ C_i = \{ x_p : \| x_p - \mu_i \| \leq \| x_p - \mu_j \|, \forall j, 1 \leq j \leq k \} \ ?Ci?={xp?:∥xp??μi?∥≤∥xp??μj?∥,?j,1≤j≤k}?

3. 更新質心：

   • 對每個簇 $(C_i)$，計算簇內所有數據點的平均值，并將該平均值作為新的質心。新的質心計算公式為：
     $${\mu }_i=\frac{1}{|C_i|}\sum _{x_j\in C_i}{x}_j$$

4. 重復：

   • 重復分配簇和更新質心的步驟，直到質心位置不再發生變化或達到最大迭代次數。

K-Means 算法的優化目標

K-Means 算法的優化目標是最小化所有數據點到其所屬簇質心的距離平方和。優化目標函數可以表示為：
$$J=\sum _{i=1}^k\sum _{x_j\in C_i}\Vert x_j?{\mu }_i{\Vert }^2$$

該目標函數也稱為聚類內的總平方誤差（Total Within-Cluster Sum of Squares，簡稱 TSS）。

K-Means 算法的優缺點

優點

1. 簡單易懂：K-Means 算法原理簡單，容易實現。
2. 速度快：算法收斂速度快，適合處理大規模數據集。
3. 適用范圍廣：在許多實際問題中表現良好。

缺點

1. 選擇 ( k ) 值的困難：需要預先指定簇的數量 ( k )，而合適的 ( k ) 值通常不易確定。
2. 對初始值敏感：初始質心的選擇會影響最終結果，可能陷入局部最優解。
3. 對異常值敏感：異常值可能會顯著影響質心的位置。

K-Means 算法的 Python 實現

下面通過 Python 代碼實現 K-Means 算法，并以一個示例數據集展示其應用。

導入庫

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeansplt.rcParams['font.sans-serif'] = ['SimHei']  # 用來正常顯示中文標簽
plt.rcParams['axes.unicode_minus'] = False  # 用來正常顯示負號

生成示例數據集

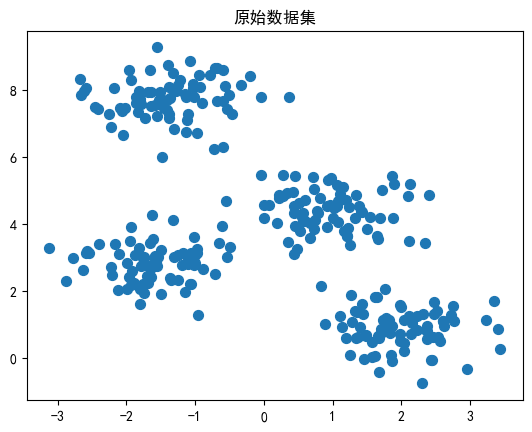
# 生成示例數據集
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show()

應用 K-Means 算法

# 應用 K-Means 算法
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)# 可視化聚類結果
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75, marker='x')
plt.show()

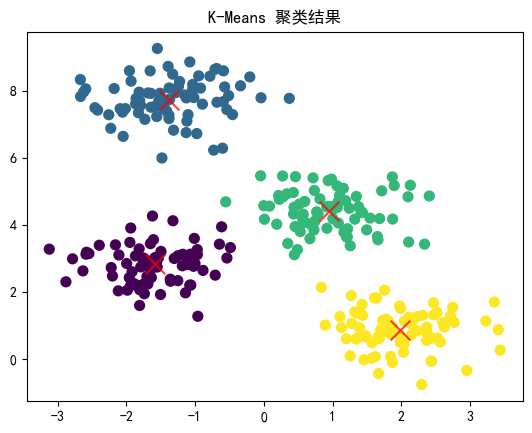
結果解釋

在上面的示例中，我們生成了一個有 4 個簇的示例數據集，并使用 K-Means 算法對其進行聚類。最終，我們通過可視化展示了聚類結果以及每個簇的質心。

總結

K-Means 算法是一種簡單而有效的聚類算法，廣泛應用于各種數據分析和機器學習任務中。本文詳細介紹了 K-Means 算法的原理、步驟、公式以及 Python 實現。雖然 K-Means 算法有一些缺點，但通過合理選擇參數和預處理數據，可以在許多實際應用中取得良好的效果。希望本文能幫助你更好地理解和應用 K-Means 算法。

我的同系列其他博客

支持向量機(SVM算法詳解)
回歸算法詳解
knn算法詳解
GBDT算法詳解
XGBOOST算法詳解
CATBOOST算法詳解
隨機森林算法詳解
lightGBM算法詳解
對比分析：GBDT、XGBoost、CatBoost和LightGBM
機器學習參數尋優：方法、實例與分析