雙指針算法第二彈（查找總價格為目標值的兩個商品-和為s的兩個數字三數之和四數之和）

系列文章目錄

《雙指針算法第一彈（移動零復寫零快樂數）》鏈接：http://t.csdnimg.cn/Nqdvn

系列文章目錄

前言

1. 查找總價格為目標值的兩個商品

（1）題目及示例

（2）思路（由淺入深）

2. 三數之和

（1）題目及示例

（2）一般思路

（2）雙指針優化

3. 四數之和

（1）題目及示例

（2）一般思路

（3）雙指針優化

總結

前言

本篇文章開啟雙指針算法第二彈，一起來感受雙指針算法的魅力。這三道OJ題思路相似，難度由易到難，可以按照下面順序自己挑戰一下。每道題目中都帶有鏈接，不用再去Leetcode尋找了！

1. 查找總價格為目標值的兩個商品

（1）題目及示例

題目：購物車內的商品價格按照升序記錄于數組 price。請在購物車中找到兩個商品的價格總和剛好是 target。若存在多種情況，返回任一結果即可。

鏈接：. - 力扣（LeetCode）

示例 1：

輸入：price = [3, 9, 12, 15], target = 18

輸出：[3,15] 或者 [15,3]

示例 2：

輸入：price = [8, 21, 27, 34, 52, 66], target = 61

輸出：[27,34] 或者 [34,27]

（2）思路（由淺入深）

分析：這道題目讓我們在給出的數組中尋找兩個數字的總和剛好是target。其中這個數組是個升序數組，已經排好序了。

如果我們用正常思維，最先想到應該是暴力解法。寫兩層for循環，第一層循環固定第一個數，第二層循環從固定數后一個數開始尋找符合題目要求的數，然后固定的數從首元素開始到倒數第二個元素結束。兩層for循環，最壞的情況是遍歷n-1，n-2，……，1，加起來就是 $N^{2}$ 級別，時間復雜度O( $N^{2}$ )，空間復雜度是O(1)。如果你把下面的代碼寫到Leetcode中去提交，大概率過不了，會超出時間限制。

    vector<int> twoSum(vector<int>& price, int target) {int n = price.size();for(int i = 0; i < n - 1; i++)for (int j = i + 1; j < n; j++)if (price[i] + price[j] == target)return {price[i], price[j]};return {-1, -1};//照顧編譯器}

我們該如何優化呢？需要注意到題目給出的數組是升序的，我們可以利用這個性質。我們使用兩個變量表示數組元素下標，用來指向數組元素。此時兩元素之和為sum。

如果其中一個變量加1，即指向后一個元素，因為數組是單調遞增的，sum的值都會增大。
如果其中一個變量減1，指向前一個元素，那么指向元素比之前的元素小，sum的值會減小。

如下圖，target等于31，left和right表示數組元素的下標。我們不讓left和right一開始都指向首元素，讓left指向首元素，right指向末尾元素。sum此時為首尾元素之和，跟target無非就大于，小于和等于三種關系。

下圖中，sum小于target。如果使用暴力解法，right需要指向第二個元素9開始，然后往后挪動，尋找匹配的元素。可末尾元素是最大的，它和首元素相加都小于target，那么中間元素加上首元素肯定也小于target。因此，此時只需要將left++，指向后一個元素，sum才會增大，繼續與target比較。

同理，此時target為37，sum大于target。如果使用暴力解法，那么left固定在末尾元素之前，都會跟末尾元素相加。首元素與末尾元素相加大于target，況且中間元素全部都比首元素大，那么中間元素加上末尾元素肯定也大于target。此時，只需要right--，指向前一個元素，使得sum減小，才有可能與target相等。

根據上面的分析再來實現代碼，是很簡單的。先定義三個變量left，right，sum，分別表示數組元素的下標和下標元素之和。使用while循環，循環條件是left小于right。
循環內部就是sum賦值為兩元素之和，然后跟target比較。當sum大于target時，需要減小肅穆，right--，同理sum小于target時，就是left++。
如果相等，直接使用花括號返回兩個元素，這樣子的形式是隱士類型轉換。
最后再循環外面再隨便返回兩個值，題目中沒有說明找不到的情況返回什么，但是不返回的話，編譯器會報錯，認為如果循環走完沒有返回值，就會出問題，所以可以隨便返回兩個值。

    vector<int> twoSum(vector<int>& price, int target) {int left = 0, right = price.size() - 1, sum = 0;while(left < right){sum = price[left] + price[right];//三種情況if (sum > target)right--;else if (sum < target)left++;elsereturn {price[left], price[right]};//return vector{price[left], price[right]};}return {-1, -1};//照顧編譯器}

2. 三數之和

（1）題目及示例

題目：給你一個整數數組 nums ，判斷是否存在三元組 [nums[i], nums[j], nums[k]] 滿足 i != j、i != k 且 j != k ，同時還滿足 nums[i] + nums[j] + nums[k] == 0 。請你返回所有和為 0 且不重復的三元組。注意：答案中不可以包含重復的三元組。

鏈接:. - 力扣（LeetCode）

示例 1：

輸入：nums = [-1,0,1,2,-1,-4]

輸出：[[-1,-1,2],[-1,0,1]]

解釋：

nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。

nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。

nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。

不同的三元組是 [-1,0,1] 和 [-1,-1,2] 。注意，輸出的順序和三元組的順序并不重要。

示例 2：

輸入：nums = [0,1,1]

輸出：[]

解釋：唯一可能的三元組和不為 0 。

示例 3：

輸入：nums = [0,0,0]

輸出：[ [0,0,0] ]

解釋：唯一可能的三元組和為 0 。

（2）一般思路

這道題我們使用暴力枚舉，寫三層for循環，找出所有的三元組合。再求和，尋找和為0的三元組。但是題目還有要求，輸出的三元組不能重復，所以還需要檢查和為0的三元組，進行去重操作。

如下圖，示例1中的數組，有三個和為0的數組，肉眼觀察就知道前兩個是重復，那程序怎么辨別呢？可以對每個符合要求的三元組進行排序，再進行比較就可以去重。
但是符合要求的三元組非常多，每一個進行排序，消耗很大，效率低。因此，可以一開始就排排升序，讓和為0的三元組按順序存放，然后再使用set自動去重，也可以手動去重。

下面的代碼就是按照上面的思路實現的。

數組先進行了排序，排序時間復雜度O( $n\log n$ )，但是使用了三層for循環，暴力枚舉出所有三元組，時間復雜度是O( $n^{3}$ )。總的時間復雜度是 O( $n\log n$ + $n^{3}$ )。在這個時間復雜度中，n^3 項是主導項，因此可以簡化為 O( $n^{3}$ )。
vector 存儲最終的三元組，最壞情況下需要 O( $n^{3}$ ) 的空間，即所有可能的組合都不重復。set 用于去重，最壞情況下也需要 O( $n^{3}$ ) 的空間，以存儲所有不重復的三元組。因此，總的空間復雜度是 O( $n^{3}$ )。

vector<vector<int>> threeSum(vector<int>& nums)
{vector<vector<int>> ret;set<vector<int>> unique; // 使用set去重sort(nums.begin(), nums.end()); // 先對數組進行排序for (int i = 0; i < nums.size(); ++i) for (int j = i + 1; j < nums.size(); ++j) for (int k = j + 1; k < nums.size(); ++k) if (nums[i] + nums[j] + nums[k] == 0) {vector<int> tmp = {nums[i], nums[j], nums[k]};unique.insert(tmp); // 將三元組插入set中，自動去重}// 將set中的三元組拷貝到結果數組中for (const auto& e : unique) ret.push_back(e);return result;
}

（2）雙指針優化

這道題其實跟上一道題解法類似，可以說是它的拓展。我們先對數組排升序，然后利用升序的性質使用雙指針。不過這次需要尋找三個數字，可以固定首元素，尋找和為首元素的相反數的兩個數。但是上一個題目只有尋找一對數。

在這道題中，如果找到一對符合要求的數字，還要繼續尋找，直到兩個變量相等，即指向同一個元素。需要注意，還要執行三個去重操作。target為固定元素的相反值，sum為left和right下標元素之和。

如下圖，先固定首元素，使用雙指針尋找和為target的兩個元素。第四個元素之前，sum小于target，所以left需要不斷加1，往后移動。直到指向第四個元素時，sum等于target，left指向前一個元素，right指向后一個元素，并且需要跳過相同的數

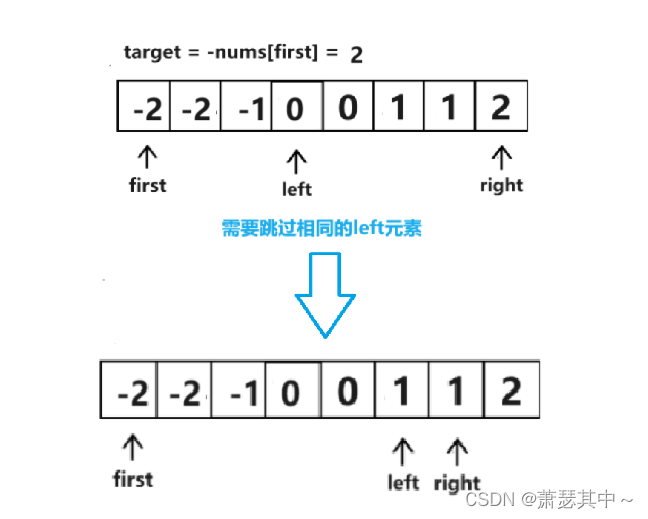
下面數組中，left和right指向的元素之和剛好為target。left++，right--，指向中間的元素，不過有兩個2，相同的元素，right需要跳過去。
此時left指向的元素值是1，right指向元素的值也是1，符合要求，會記錄下來。left和right指向的元素相鄰，說明這一輪已經結束。first需要指向后面的元素，并且它也要跳過相同的元素，避免重復。

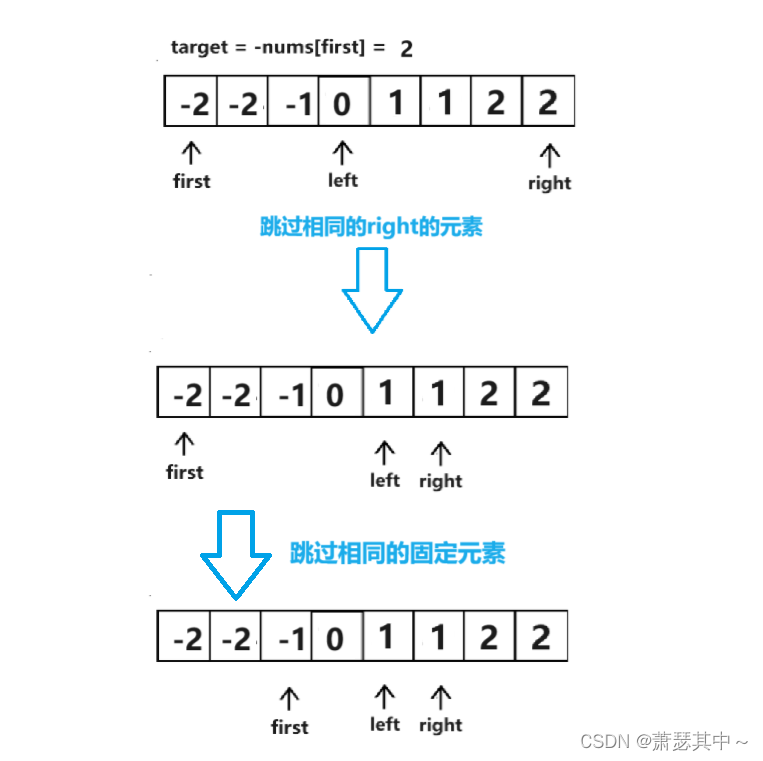
當我們知道需要三個去重操作之后，再去實現代碼就比較容易。

其中排序消耗的時間復雜度是O( $n\log n$ )，兩層for循環的時間復雜度是O( $n^2{}$ )，綜合起來，時間復雜度是O( $n^2{}$ )。
空間上，使用了幾個變量，還使用ret數組，數組的大小取決于輸入數組中三元組的數量，最多也是O( $n^2{}$ )。
首先對數組進行排序。其次使用for循環，固定首元素，直到倒數第三個元素。i表示固定元素的下標，我們一開始就判斷，固定的元素跟前一個元素是否重復，重復就跳過，并且要注意先判斷i大于0，不然會越界訪問到前面內存空間并報錯。
for循環內部就是尋找和為target的二元組，跟第一道題目類似。只不過再找到一個二元組時，也需要跳過重復的數字，進行去重操作。這里也需要注意while循環中繼續的條件，先寫left<right，這個是保證兩個變量相等時，不會發生對數組的元素發生二次遍歷。

vector<vector<int>> threeSum(vector<int>& nums) 
{sort(nums.begin(), nums.end());//對數組進行排序int n = nums.size();vector<vector<int>> ret;for (int i = 0; i < n - 2; ++i) {if (i > 0 && nums[i] == nums[i - 1]) continue; // 跳過重復的iint target = -nums[i];int left = i + 1, right = n - 1;while (left < right) {int sum = nums[left] + nums[right];if (sum < target) ++left;else if (sum > target) --right;else {                  ret.push_back({nums[i], nums[left], nums[right]});++left;while (left < right && nums[left] == nums[left - 1]) ++left; // 跳過重復的left--right;while (left < right && nums[right] == nums[right + 1]) --right; // 跳過重復的right}}}return ret;
}

3. 四數之和

（1）題目及示例

題目：給你一個由 n 個整數組成的數組?nums ，和一個目標值 target 。請你找出并返回滿足下述全部條件且不重復的四元組?[nums[a], nums[b], nums[c], nums[d]]?（若兩個四元組元素一一對應，則認為兩個四元組重復）：

0 <= a, b, c, d?< n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意順序 返回答案。

鏈接：. - 力扣（LeetCode）

示例 1：

輸入：nums = [1,0,-1,0,-2,2], target = 0

輸出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

輸入：nums = [2,2,2,2,2], target = 8

輸出：[[2,2,2,2]]

（2）一般思路

這道題目是三數之和的升級，尋找符合要求的四個數。

暴力解法也類似，先進行排序，再嵌套四層for循環，枚舉出所有四元組，再求和比較是否與target相等。使用set去重，或者手動去重。這里就不在寫代碼了。

暴力解法中，使用sort排序時間復雜度O( $n\log n$ )，再使用了四層for循環，枚舉出所有四元組，時間復雜度是O( $n^{4}$ )。總的來說，時間復雜度就是O( $n^{4}$ )。

（3）雙指針優化

四數之和，是三數之和的延伸。兩道題思路大體是一樣的，先寫兩層for循環來固定兩個數，下標分別為i和j，然后再轉換成尋找和為target-nums[i]-nums[j]的二元組，又變成了如何解決第一道題目。不過這道題需要去重的地方有四處。

first固定第一個數，跳過重復元素。
second固定第二個數，跳過重復元素。
left和right雙指針，跳過重復元素。

實現代碼時，需要注意Leetcode給出的測試用例中，target超出int整型范圍，會造成溢出，需要換成long long來定義變量。

    vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(), nums.end());//對數組進行排序int n = nums.size();vector<vector<int>> ret;//存儲四元組for (int i = 0; i < n - 3; ++i) //固定第一個數{if (i > 0 && nums[i - 1] == nums[i])//跳過重復的數字continue;//利用三數之和for (int j = i + 1; j < n - 2; ++j) //固定第二個數{if (j > i + 1 && nums[j - 1] == nums[j])//跳過重復的數字，需要注意不能寫成j>0continue;int left = j + 1, right = n - 1;//示例target太大，會整型溢出，用long long類型轉換一下long long aim = (long long)target - nums[i] - nums[j];// 利用雙指針解決while(left < right){int sum = nums[left] + nums[right];if (sum > aim)--right;else if (sum < aim)++left;else{ret.push_back({nums[i], nums[j], nums[left], nums[right]});++left;while(left < right && nums[left] == nums[left - 1])++left;// 跳過重復的left--right;while(left < right && nums[right] == nums[right + 1])--right;// 跳過重復的right}}}}return ret;}