ai目錄：sheng的學習筆記-AI目錄-CSDN博客?

需要學習前置知識：聚類，可參考??sheng的學習筆記-聚類(Clustering)-CSDN博客

目錄

什么是k均值算法

流程

偽代碼

數據集

偽代碼?

代碼解釋

劃分示意圖

優化目標?

隨機初始化

選擇聚類數

---

什么是k均值算法

K-均值（K-Means Algorithm）是最普及的聚類算法，算法接受一個未標記的數據集，然后將數據聚類成不同的組。

流程

K-均值是一個迭代算法，假設我們想要將數據聚類成n個組，其方法為:

1. 首先選擇個隨機的點，稱為聚類中心（cluster centroids）；
2. 對于數據集中的每一個數據，按照距離個中心點的距離，將其與距離最近的中心點關聯起來，與同一個中心點關聯的所有點聚成一類。
3. 計算每一個組的平均值，將該組所關聯的中心點移動到平均值的位置。
4. 重復步驟。

示例圖如下?

迭代 1 次

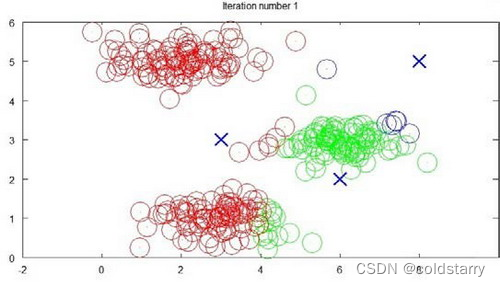
迭代 3?次

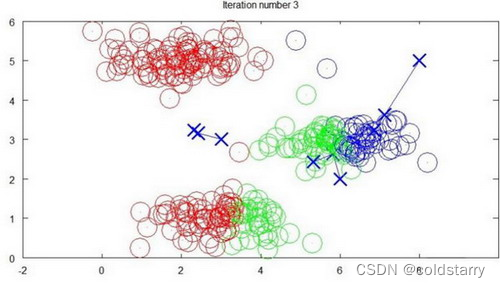
迭代 10?次

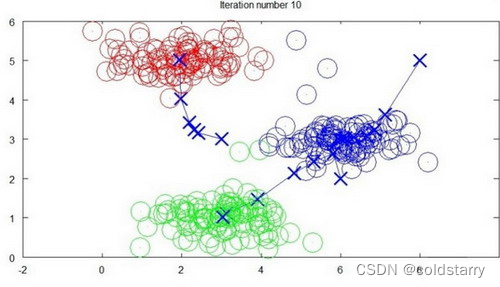
偽代碼

樣本9～21的類別是“好瓜=否”，其他樣本的類別是“好瓜=是”。由于本節使用無標記樣本，因此類別標記信息未在表中給出。為避免運行時間過長，通常設置一個最大運行輪數或最小調整幅度閾值，若達到最大輪數或調整幅度小于閾值，則停止運行。下面以表9.1的西瓜數據集4.0為例來演示k均值算法的學習過程。為方便敘述，我們將編號為i的樣本為xi，這是一個包含“密度”與“含糖率”兩個屬性值的二維向量

數據集

偽代碼?

代碼解釋

算法分為兩個步驟，第一個for循環是賦值步驟，即：對于每一個樣例，計算其應該屬于的類。第二個for循環是聚類中心的移動，即：對于每一個類，重新計算該類的質心

1）假定聚類簇數k=3，算法開始時隨機選取三個樣本x6,x12,x24作為初始均值向量，即：

μ1=(0.403;0.237),μ2=(0.343;0.099),μ3=(0.478;0.437)。

2）考察樣本x1=(0.697;0.460)，它與當前均值向量μ1，μ2，μ3的距離分別為0.369,0.506,0.220，因此x1將被劃入簇C3中。類似的，對數據集中的所有樣本考察一遍后，可得當前簇劃分為

C1={x3,x5,x6,x7,x8,x9,x10,x13,x14,x17,x18,x19,x20,x23};

C2={x11,x12,x16）;

C3={x1,x2,x4,x15,x21,x22,x24,x25,x26,x27,x28,x29,x30};

3）于是，可從C1,C2,C3分別求出新的均值向量

4）?更新當前均值向量后，不斷重復上述過程，如圖9.3所示，第五輪迭代產生的結果與第四輪迭代相同，于是算法停止，得到最終的簇劃分

劃分示意圖

優化目標?

隨機初始化

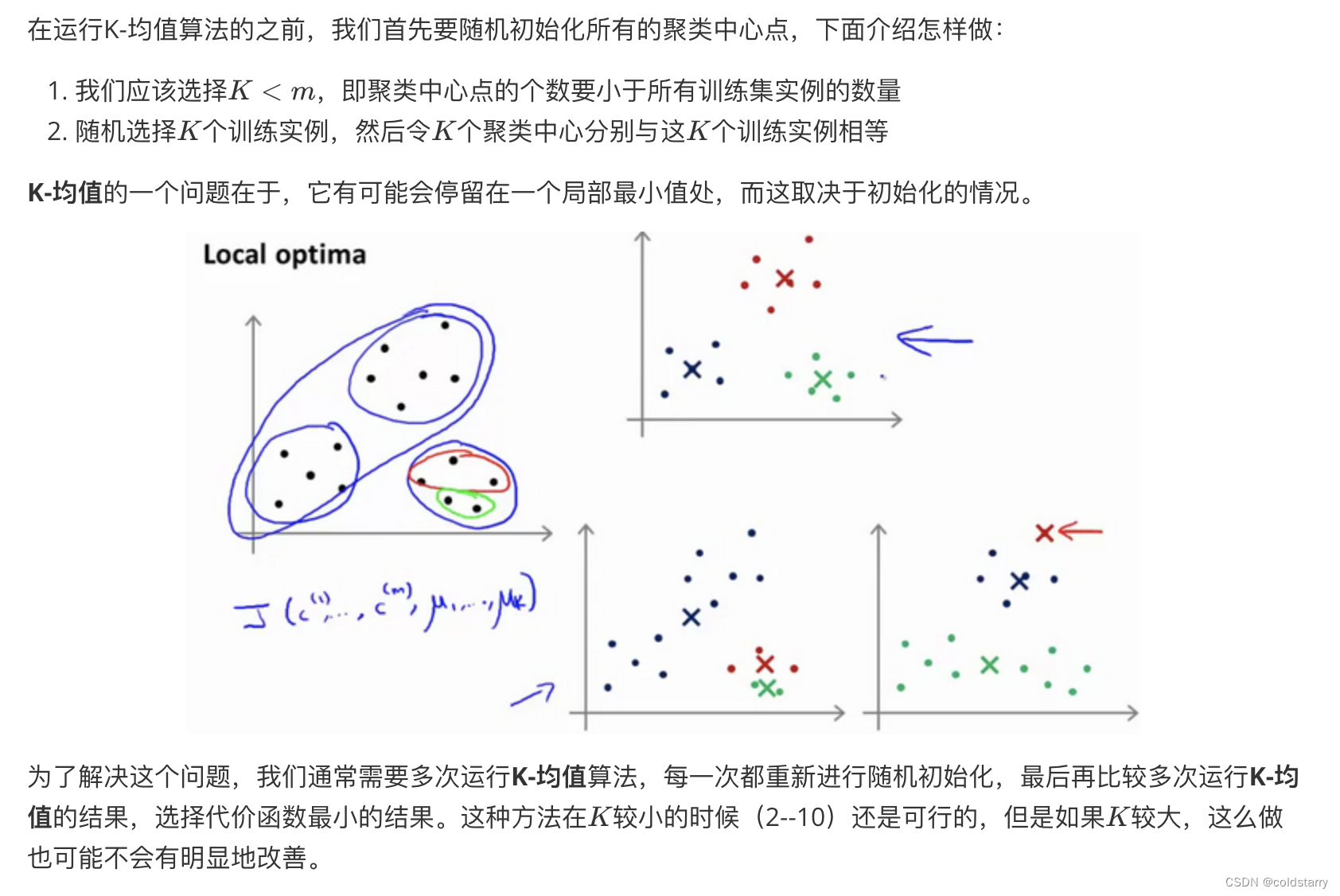
選擇聚類數

沒有所謂最好的選擇聚類數的方法，通常是需要根據不同的問題，人工進行選擇的。選擇的時候思考我們運用K-均值算法聚類的動機是什么，然后選擇能最好服務于該目的標聚類數。

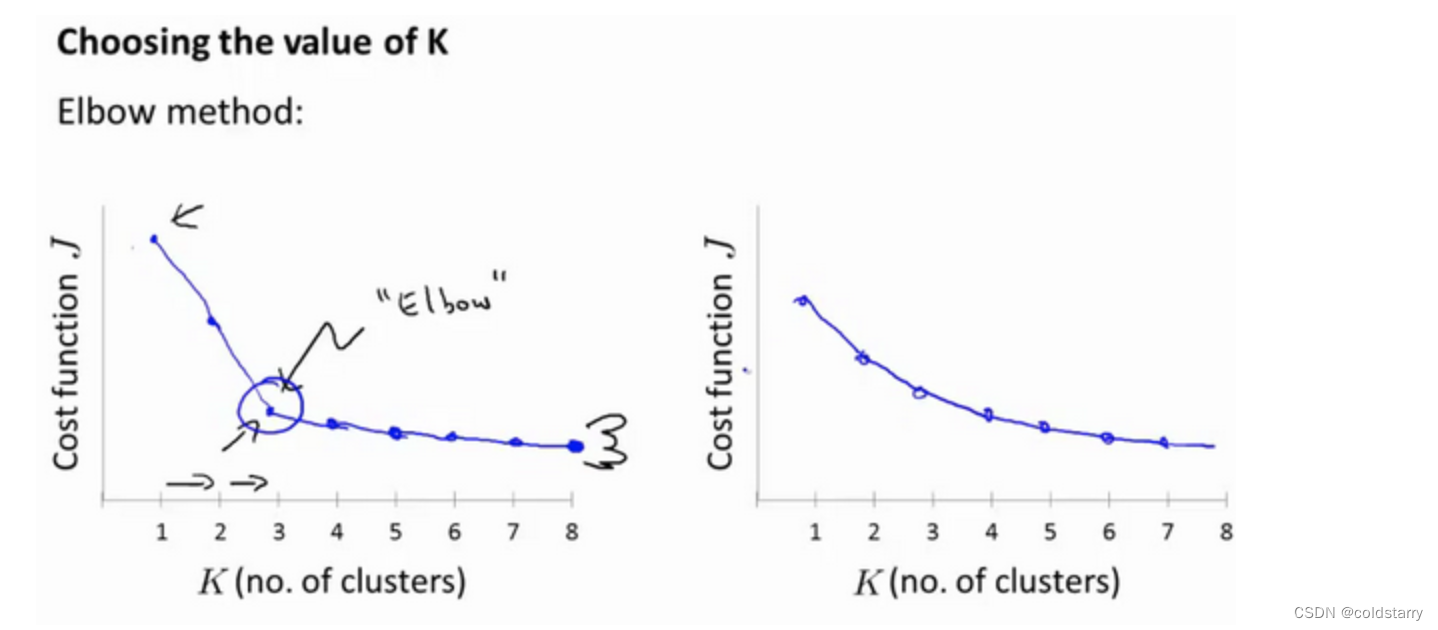
當人們在討論，選擇聚類數目的方法時，有一個可能會談及的方法叫作“肘部法則”。關于“肘部法則”，我們所需要做的是改變K值，也就是聚類類別數目的總數。我們用一個聚類來運行K均值聚類方法。這就意味著，所有的數據都會分到一個聚類里，然后計算成本函數或者計算畸變函數J。K代表聚類數字

我們可能會得到一條類似于這樣的曲線。像一個人的肘部。這就是“肘部法則”所做的，讓我們來看這樣一個圖，看起來就好像有一個很清楚的肘在那兒。好像人的手臂，如果你伸出你的胳膊，那么這就是你的肩關節、肘關節、手。這就是“肘部法則”。你會發現這種模式，它的畸變值會迅速下降，從1到2，從2到3之后，你會在3的時候達到一個肘點。在此之后，畸變值就下降的非常慢，看起來就像使用3個聚類來進行聚類是正確的，這是因為那個點是曲線的肘點，畸變值下降得很快，K=3之后就下降得很慢，那么我們就選K=3。當你應用“肘部法則”的時候，如果你得到了一個像上面這樣的圖，那么這將是一種用來選擇聚類個數的合理方法。

例如，我們的 T-恤制造例子中，我們要將用戶按照身材聚類，我們可以分成3個尺寸:S,M,L，也可以分成5個尺寸XS,S,M,L,XL，這樣的選擇是建立在回答“聚類后我們制造的T-恤是否能較好地適合我們的客戶”這個問題的基礎上作出的。

參考文章：

吳恩達機器學習

書：機器學習? ?周志華