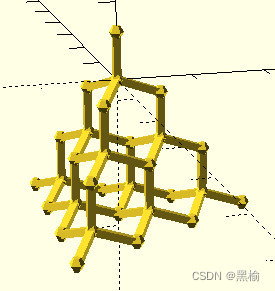
在30個點的4面體空間內取4個點，有30*29*28*27/24=27405種取法，要求得到的4個點必須在直鏈上。只有144個結構符合要求，在平移操作下不重合的結構有36個。
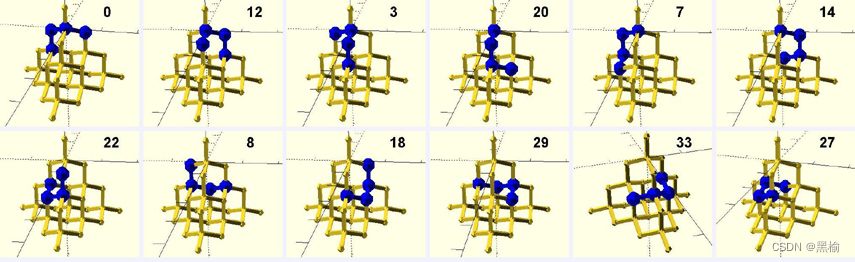
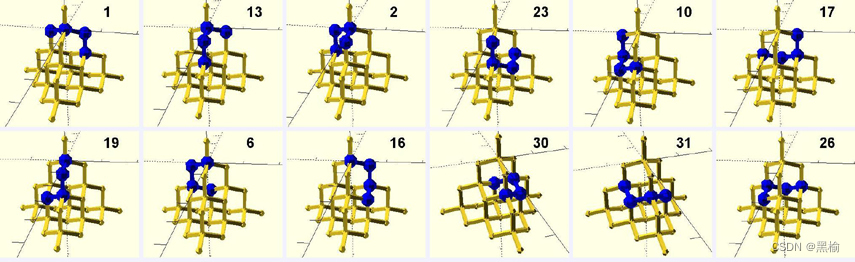
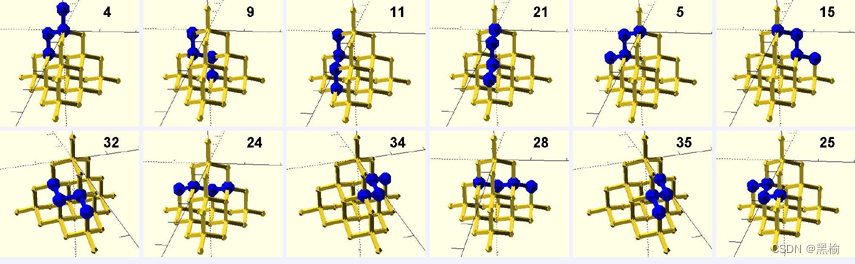
這36個結構可以按照旋轉對稱性進一步分成3組0，1，4，每組12個
| A | B | C | D | ||||||||
| 0 | 120 | 240 | 0 | 120 | 240 | 0 | 120 | 240 | 0 | 120 | 240 |
| 0 | 12 | 3 | 20 | 7 | 14 | 22 | 8 | 18 | 29 | 33 | 27 |
| 1 | 13 | 2 | 23 | 10 | 17 | 19 | 6 | 16 | 30 | 31 | 26 |
| 4 | 9 | 11 | 21 | 5 | 15 | 32 | 24 | 34 | 28 | 35 | 25 |
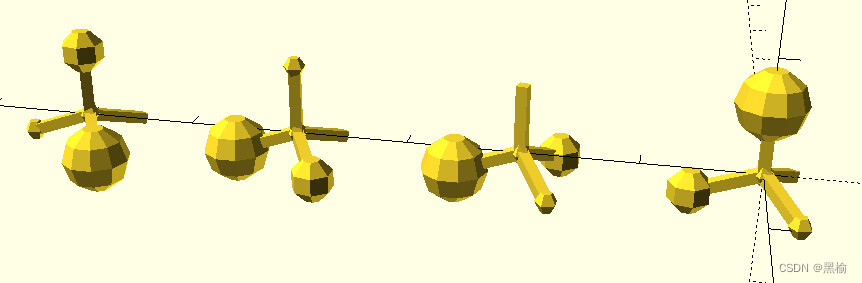
將4個頂點先后朝上，再繞軸旋轉0，120，240度。
左側0右側2，結構0和2互為鏡像
顯然0，1是鄰位，4是對位。
| 組合 | 隨機 | 隨機 | |||||
| 27405 | 144 | 50000 | 293 | 100000 | 513 | ||
| 0.0053 | 0.0059 | 0.0051 | |||||
| 結構 | 數量 | 結構 | 數量 | 結構 | 數量 | ||
| 0 | 4 | 0 | 7 | 0 | 9 | ||
| 1 | 4 | 1 | 9 | 1 | 15 | ||
| 2 | 4 | 2 | 7 | 2 | 21 | ||
| 3 | 4 | 3 | 8 | 3 | 19 | ||
| 4 | 4 | 4 | 5 | 4 | 9 | ||
| 5 | 4 | 5 | 8 | 5 | 8 | ||
| 6 | 4 | 6 | 4 | 6 | 15 | ||
| 7 | 4 | 7 | 9 | 7 | 10 | ||
| 8 | 4 | 8 | 8 | 8 | 8 | ||
| 9 | 4 | 9 | 12 | 9 | 9 | ||
| 10 | 4 | 10 | 12 | 10 | 23 | ||
| 11 | 4 | 11 | 6 | 11 | 12 | ||
| 12 | 4 | 12 | 5 | 12 | 14 | ||
| 13 | 4 | 13 | 10 | 13 | 15 | ||
| 14 | 4 | 14 | 6 | 14 | 21 | ||
| 15 | 4 | 15 | 9 | 15 | 12 | ||
| 16 | 4 | 16 | 3 | 16 | 18 | ||
| 17 | 4 | 17 | 9 | 17 | 13 | ||
| 18 | 4 | 18 | 10 | 18 | 19 | ||
| 19 | 4 | 19 | 7 | 19 | 11 | ||
| 20 | 4 | 20 | 8 | 20 | 19 | ||
| 21 | 4 | 21 | 9 | 21 | 9 | ||
| 22 | 4 | 22 | 3 | 22 | 16 | ||
| 23 | 4 | 23 | 7 | 23 | 12 | ||
| 24 | 4 | 24 | 4 | 24 | 19 | ||
| 25 | 4 | 25 | 8 | 25 | 8 | ||
| 26 | 4 | 26 | 10 | 26 | 15 | ||
| 27 | 4 | 27 | 11 | 27 | 12 | ||
| 28 | 4 | 28 | 3 | 28 | 22 | ||
| 29 | 4 | 29 | 14 | 29 | 14 | ||
| 30 | 4 | 30 | 12 | 30 | 16 | ||
| 31 | 4 | 31 | 15 | 31 | 11 | ||
| 32 | 4 | 32 | 6 | 32 | 12 | ||
| 33 | 4 | 33 | 11 | 33 | 21 | ||
| 34 | 4 | 34 | 7 | 34 | 10 | ||
| 35 | 4 | 35 | 11 | 35 | 16 |
統計占比，這里所有的36個結構每個都只有4個，所以0，1，4的占比相同都是1/3.
隨機了5萬次，10萬次驗算。
所以如果已知某一空間內只有0，1，4這3種4點直鏈結構，并且其占比都相同，則有理由猜測這個空間內的點是按照甲烷的方式聯絡在一起。在這樣的空間內直鏈4點結構隨機運動可能呈現的結構只能是0，1，4這3種，并且占比一定相同。
如果在某一空間內有結構0，1占比30%，4占比70%。有理由猜測其所在空間點的聯絡方式可能為
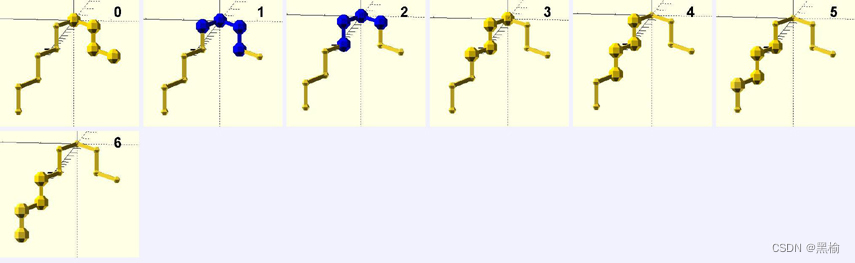
這個空間內有對位5個，鄰位2個
這個空間內有對位4個，鄰位2個-
如果二者的占比是6：4，則有6*5+4*4=46個對位有20個鄰位，鄰位占比為20/66約為0.303.
)
