第21天，二叉樹最后一篇，沖💪

目錄

669.修建二叉搜索樹

108.將有序數組轉換為二叉搜索樹

538.把二叉搜索樹轉換為累加樹

二叉樹總結

---

669.修建二叉搜索樹

文檔講解：代碼隨想錄修建二叉搜索樹

視頻講解：手撕修建二叉搜索樹

題目：

學習：

本題需要注意的點很多，不能夠輕易的就把節點刪除，首先：1.本題給出的最小邊界值和最大邊界值，不一定會存在樹中，只是提供一個區間大小，因此不能夠節點判斷是否等于low或者high。2.在找到小于low的值后不能夠直接將其刪除，因為它的右孩子不一定小于low，同理大于high的節點也不能直接刪除，還需要關注它的左孩子。3.在2的基礎上，也不能直接把右孩子返回，因為右孩子大于low的情況下，右孩子的左孩子還是可能會小于low需要刪除，因此還需要不斷的進行遍歷。（該情況如下圖所示，如果區間在[2,3]之間）

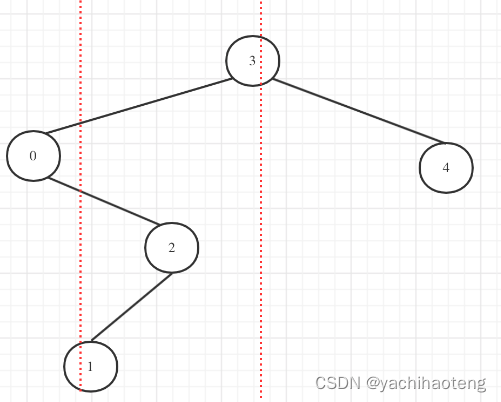
依據上述所說，來設計遞歸三部曲。

代碼：

//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
public://確定返回值，本題需要重新構造二叉樹節點，因此使用返回值更加方便，當然也可以沒有返回值就需要手動進行左右孩子構造TreeNode* trimBST(TreeNode* root, int low, int high) {//確定終止條件if (root == nullptr) return nullptr;//確定單層遞歸邏輯（核心是將root轉移到low和high區間內）//1.當前值大于highif (root->val > high) {//在該節點左邊找尋是否有合適的值return trimBST(root->left, low, high);}//2.當前值小于lowif (root->val < low) {//在該節點右邊找尋是否有合適的值return trimBST(root->right, low, high);}//3.當前值在low和high區間內，但是還不能就此下定義，還需要判斷該節點左右孩子是否合格root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);//持續把修改后的節點返回上層return root;}
};

代碼：本題也能夠使用迭代法，且由于二叉搜索樹自帶遍歷條件，因此不需要額外空間。

//時間復雜度O(n)
//空間復雜度O(1)
class Solution {
public:TreeNode* trimBST(TreeNode* root, int L, int R) {if (!root) return nullptr;// 處理頭結點，讓root移動到[L, R] 范圍內，注意是左閉右閉while (root != nullptr && (root->val < L || root->val > R)) {if (root->val < L) root = root->right; // 小于L往右走else root = root->left; // 大于R往左走}TreeNode *cur = root;// 此時root已經在[L, R] 范圍內，處理左孩子元素小于L的情況while (cur != nullptr) {while (cur->left && cur->left->val < L) {cur->left = cur->left->right;}cur = cur->left;}cur = root;// 此時root已經在[L, R] 范圍內，處理右孩子大于R的情況while (cur != nullptr) {while (cur->right && cur->right->val > R) {cur->right = cur->right->left;}cur = cur->right;}return root;}
};

---

108.將有序數組轉換為二叉搜索樹

文檔講解：代碼隨想錄將有序數組轉換為二叉搜索樹

視頻講解：手撕將有序數組轉換為二叉搜索樹

題目：

學習：

注意本題需要構造的不僅是二叉搜索樹還需要是一顆平衡二叉樹。平衡二叉樹需要所有中間節點的左右孩子的高度差不大于1。

依據上述條件，又因為本題給的數組已經是一個升序排列的數組了，因此本題顯然是從中間節點進行構造，每次取數組的中間節點，即可構造出平衡的二叉搜索樹。注意如果數組是奇數，顯然選中間的節點，如果數組是偶數則中間的兩個節點選哪個都可以，只要統一就行，最后構造出的二叉樹會有所區別，這也是本題答案不唯一的原因。

代碼：

//時間復雜度O(n)
//空間復雜度O(n^2)
class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {//確定終止條件if(nums.size() == 0) return nullptr;//取中間值int mid = nums.size()/2;TreeNode* node = new  TreeNode(nums[mid]);//左區間vector<int> left(nums.begin(), nums.begin() + mid);//右區間vector<int> right(nums.begin() + mid + 1, nums.end());//分配左右子樹node->left = sortedArrayToBST(left);node->right = sortedArrayToBST(right);return node;}
};

代碼：不使用額外空間，下標確定數組區間

//時間復雜度O(n)
//空間復雜度O(n)遞歸產生的棧空間
class Solution {
public://不使用額外空間，下標法TreeNode* traversal(vector<int>& nums, int left, int right) {//確定終止條件(區間左閉右閉)if(left > right) return nullptr;//找到中間值int mid = left + (right - left)/2; //防止數值越界TreeNode* node = new TreeNode(nums[mid]);//左區間node->left = traversal(nums, left, mid - 1);//右區間node->right = traversal(nums, mid + 1, right);return node;}TreeNode* sortedArrayToBST(vector<int>& nums) {return traversal(nums, 0, nums.size() - 1);}
};

538.把二叉搜索樹轉換為累加樹

文檔講解：代碼隨想錄把二叉搜索樹轉換為累加樹

視頻講解：手撕把二叉搜索樹轉換為累加樹

題目：

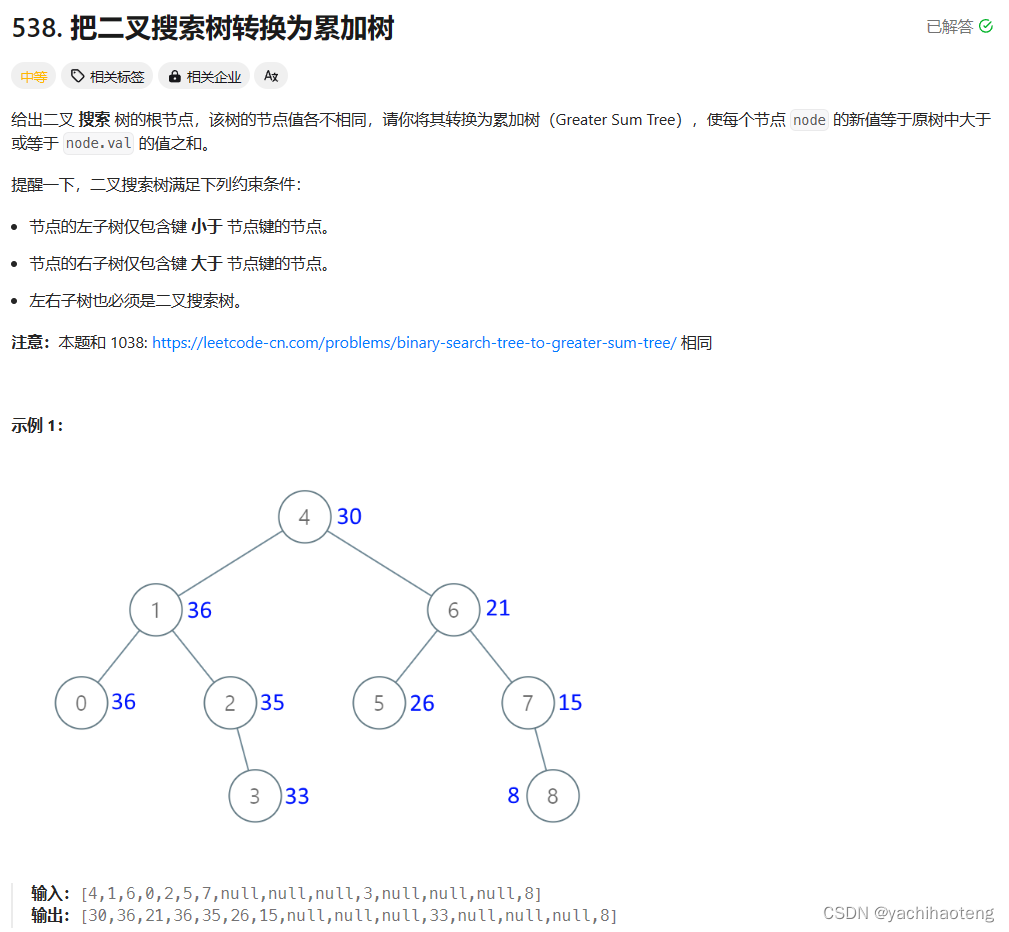
學習：本題最重要的是需要找到它的規律，本題是將每個節點的新值轉變為等于原樹中大于或等于node.val的值之和。如果將二叉搜索樹通過中序遍歷轉化為數組來看的話，其實就是從后往前依次累加。因此本題應該采用的遍歷方法是反中序遍歷，通過右中左的遍歷順序，因此將節點值累加。

注意本題累加過程中，采用的是雙指針的方法，需要一個指向當前節點的前一個節點pre來保存上一個節點的累加和。

代碼：

//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
public:TreeNode* pre = nullptr; //指向當前節點的前一個節點//本題不需要返回值，只用將當前值改變就行void traversal(TreeNode* root) {//終止條件if(root == nullptr) return;//本題的遍歷順序應該為右中左//右traversal(root->right);//中if(pre != nullptr) {root->val = root->val + pre->val;}pre = root;//左traversal(root->left);}TreeNode* convertBST(TreeNode* root) {traversal(root);return root;}
};

代碼：本題也能夠使用迭代法進行

//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
private:int pre; // 記錄前一個節點的數值void traversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->right;   // 右} else {cur = st.top();     // 中st.pop();cur->val += pre;pre = cur->val;cur = cur->left;    // 左}}}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};

二叉樹總結

對于二叉樹來說我們首先需要掌握的就是遞歸這一算法，確定遞歸三部曲掌握通過遞歸進行的二叉樹的前序遍歷、中序遍歷、后序遍歷的方法。

其次對于二叉樹來說，它的迭代方法同樣也很重要，遞歸由于其不斷遞歸的特殊性，稍有不慎就容易導致棧溢出，且問題相對于迭代法不好排查。因此掌握迭代法對于實際工程使用也十分重要。

這七天我們對二叉樹的遍歷方式，各種屬性，二叉樹的修改和構造都進行了詳細的練習。并且對二叉樹中一個重要的類型二叉搜索樹也進行了詳細的考察，二叉搜索樹自帶的遍歷順序，能夠便于解答很多問題，同時對二叉搜索樹進行中序遍歷能夠得到一個非遞減序列也是重要的性質之一。

總結來說：

• 涉及到二叉樹的構造，無論普通二叉樹還是二叉搜索樹一定都是先構造中節點。

• 求普通二叉樹的屬性，一般是后序，一般要通過遞歸函數的返回值做計算。（包括是否對稱，求最大深度，最小深度，有多少個節點，是否平衡，路徑問題，左葉子之和、左下角的值等）

• 求二叉搜索樹的屬性，一定是中序了，要不白瞎了有序性了。

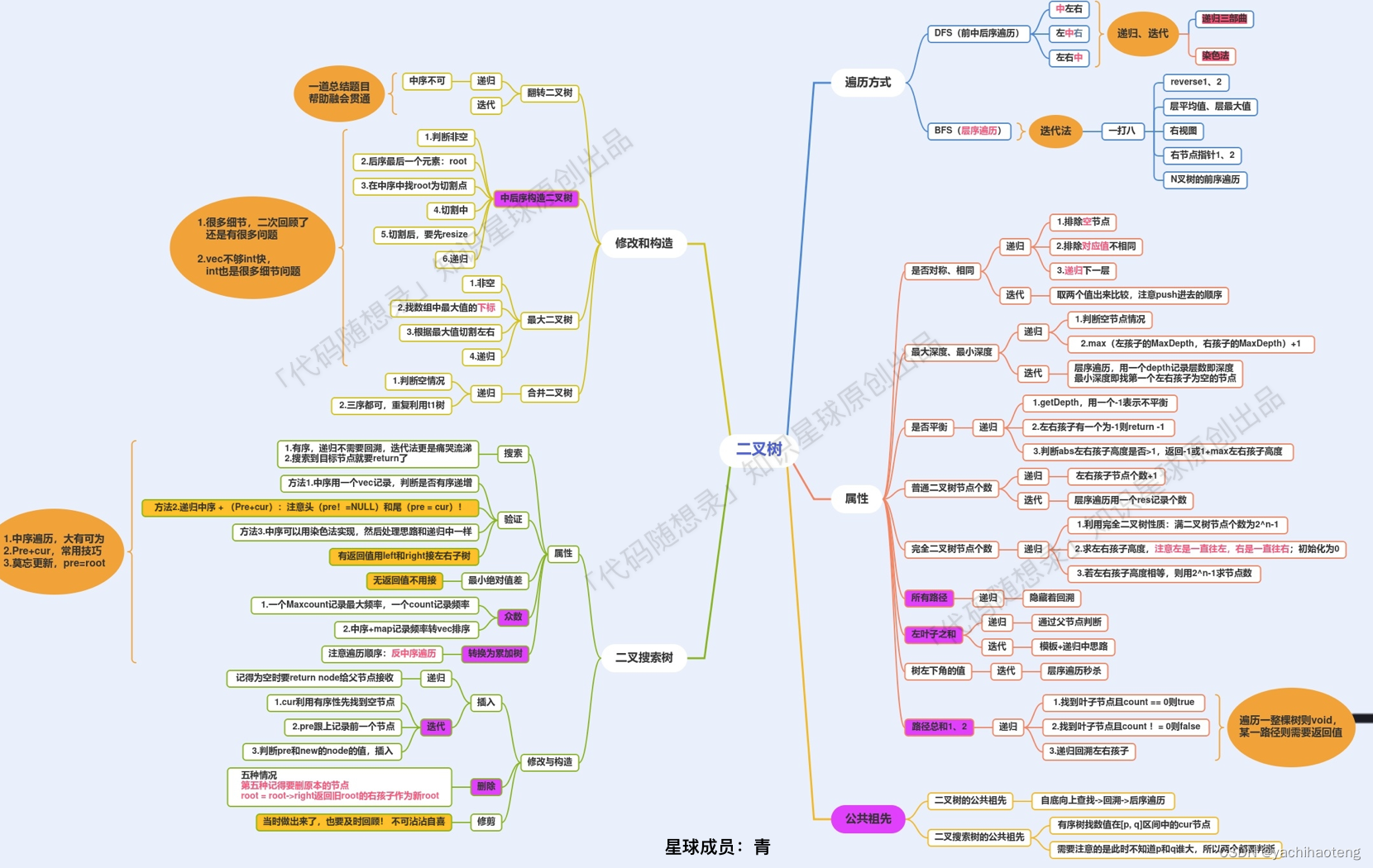
?二叉樹系列就這么完美結束了！