前面描述 卷積，本文由卷積引入拉普拉斯變換。

拉普拉斯變換就是給傅里葉變換的 iωt 加了個實部，也可以反著理解，原函數乘以 $e^{?\beta t}$ 再做傅里葉變換，本質上都是傅里葉變換的擴展。

加入實部的拉普拉斯變換在復平面展開，因此拉普拉斯變換除了有虛部的頻率特性，還有實部的衰減特性。但不管怎么說，和傅里葉變換一樣，它們均將時域分析轉換為頻域分析，這就是我經常采用的策略，橫豎一顛倒，晴空萬里。

看一個頻域的運算特性，為什么時域的卷積運算可以轉換為頻域的乘法運算？看下圖：

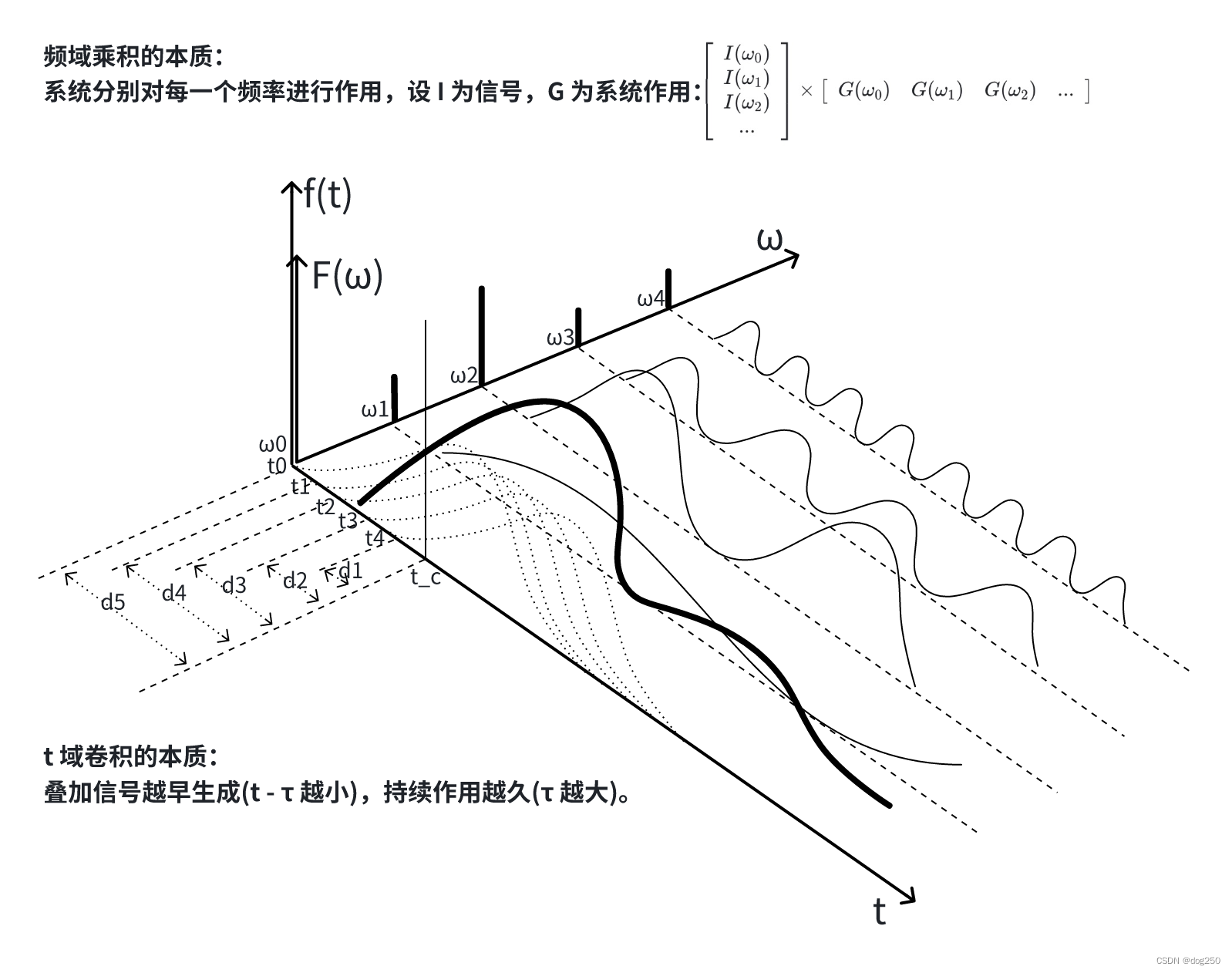
時域中，信號持續時間和信號生成時間是相對的，必須卷起來運算，而頻域是個對稱的空間維度，不同頻率信號以及針對每個頻率信號的處理全都 “擺在那里”，因此可通過精巧陣法一下子算出來(如上圖矩陣只是一個說明，本質上還是復數的乘法)。

展示一張實操圖：

以 g/G 往 f/F 涂顏料為例，上圖的卷積操作需要一邊卷緊紙一邊在 f 曲線上色，這也體現了時間域的特征，而下圖的乘積操作則是一個空間域并行操作，顏料涂在 G 半邊的曲線，對折一次就能將 F 半邊染色。

再看拉普拉斯變換對運算的實際簡化效果。

設 u 為輸入，g 為系統作用函數，時域上 u * g 的卷積獲得輸出 x，由上面的時域，頻域轉換分析獲知，拉普拉斯變換將卷積化為了乘法，即 F*G，再經拉普拉斯逆變換就能獲得 x(t) 的以下形式：

• 若特征根沒有虛部，要么是 $x(t)=e^{at}\pm e^{bt}\pm e^{ct}...$，要么收斂，要么發散，無震蕩；
• • 若有虛部，歐拉公式，要么是 $x(t)=e^{at}(\sin (bt)...)$，a > 0，震蕩發散，a < 0，震蕩收斂，a = 0，持續震蕩。

發散的都不穩定，收斂的都穩定，區別在于是否震蕩。

無需太過于關注極點的物理意義，拉普拉斯變換作為工具就只當它為工具，至于物理意義，一百個物理場景就能有一百個物理意義。

將極點看作逆變換后 x(t) 收斂，發散，震蕩特征的總結是高尚的，而不是反過來。從 x(t) 的表達式可明確歸納出 a，b，c 等系數和函數收斂，發散，震蕩的關系，而 a，b，c 等系數恰恰就是逆變換前 G(s) 分母為 0 的特征方程解的組成，將這些解在復平面的位置稱作 “極點”。

因此根據 x(t) 的收斂，發散，震蕩特性與極點實部虛部一一對應關系，通過分析 G(s) 的極點位置就能直接獲得系統特性，無需再進行逆變換：

• 有極點實部 > 0，發散不穩定，因為 e 的正次方總趨向無窮大；
• 所有極點實部 < 0，收斂穩定，收斂速度取決于絕對值；
• 極點虛部 ≠ 0，系統震蕩，因為 x(t) 包含一個 sin/cos。

這就是拉普拉斯變換 G(s) 作為工具的意義，稱 G 為傳遞函數。

浙江溫州皮鞋濕，下雨進水不會胖。