第二十天,二叉樹part07,二叉樹搜索樹加油加油💪
目錄
235.二叉搜索樹的最近公共祖先
701.二叉搜索樹中的插入操作
450.刪除二叉搜索樹中的節點
拓展:普通二叉樹的刪除方式?
總結
235.二叉搜索樹的最近公共祖先
文檔講解:代碼隨想錄二叉搜索樹的最近公共祖先
視頻講解:手撕二叉搜索樹的最近公共祖先
題目:

學習:
昨天我們是在普通二叉樹內找到公共祖先,采取的是后序遍歷的方式,遍歷所有的節點,直到找到目標值為止進行返回。
但本題是二叉搜索樹,我們可以利用二叉搜索樹的特點來進行公共祖先的查找。我們知道二叉搜索樹中每個節點的左子樹中的所有值一定小于該節點,右子樹中的所有值一定大于該節點。依據此特點我們可以把遍歷過程分為三種情況。
- p節點的值和q節點的值都小于當前遍歷節點的值,則在當前節點的左子樹進行尋找。
- p節點的值和q節點的值都大于當前遍歷節點的值,則在當前節點的右子樹進行尋找。
- p節點的值和q節點的值其中一個等于當前遍歷節點的值,或者分別大于,小于當前遍歷節點的值,則立馬返回當前遍歷的節點,該節點就是最小公共祖先。原因:①如果當前節點是p節點或者q節點的其中一個,由于我們是從上至下遍歷的,因此剩下一個節點肯定在該節點的子樹中,因此當前節點就是最小公共祖先。②當前節點不是p節點或者q節點,此時由于p節點和q節點分別位于當前節點的左右子樹之中,因此當前節點肯定是最小公共祖先,否則往左遍歷將錯過右子樹中的節點,往右遍歷將錯過左子樹中的節點。
代碼:遞歸法
//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
private:TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {if (cur == NULL) return cur;// 中if (cur->val > p->val && cur->val > q->val) { // 左TreeNode* left = traversal(cur->left, p, q);return left;}else if (cur->val < p->val && cur->val < q->val) { // 右TreeNode* right = traversal(cur->right, p, q);return right;}else { //第三種情況return cur;}}
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return traversal(root, p, q);}
};代碼:迭代法
//時間復雜度O(n)
//空間復雜度O(1)
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == NULL) return NULL;TreeNode* answer = root; //返回數組while(answer) {//依據二叉搜索樹的特點,分為三種情況if(p->val > answer->val && q->val > answer->val) {answer = answer->right;}else if(p->val < answer->val && q->val < answer->val) {answer = answer->left;}else { //第三種情況break;}}return answer;}
};701.二叉搜索樹中的插入操作
文檔講解:代碼隨想錄二叉搜索樹中的插入操作
視頻講解:手撕二叉搜索樹中的插入操作
題目:
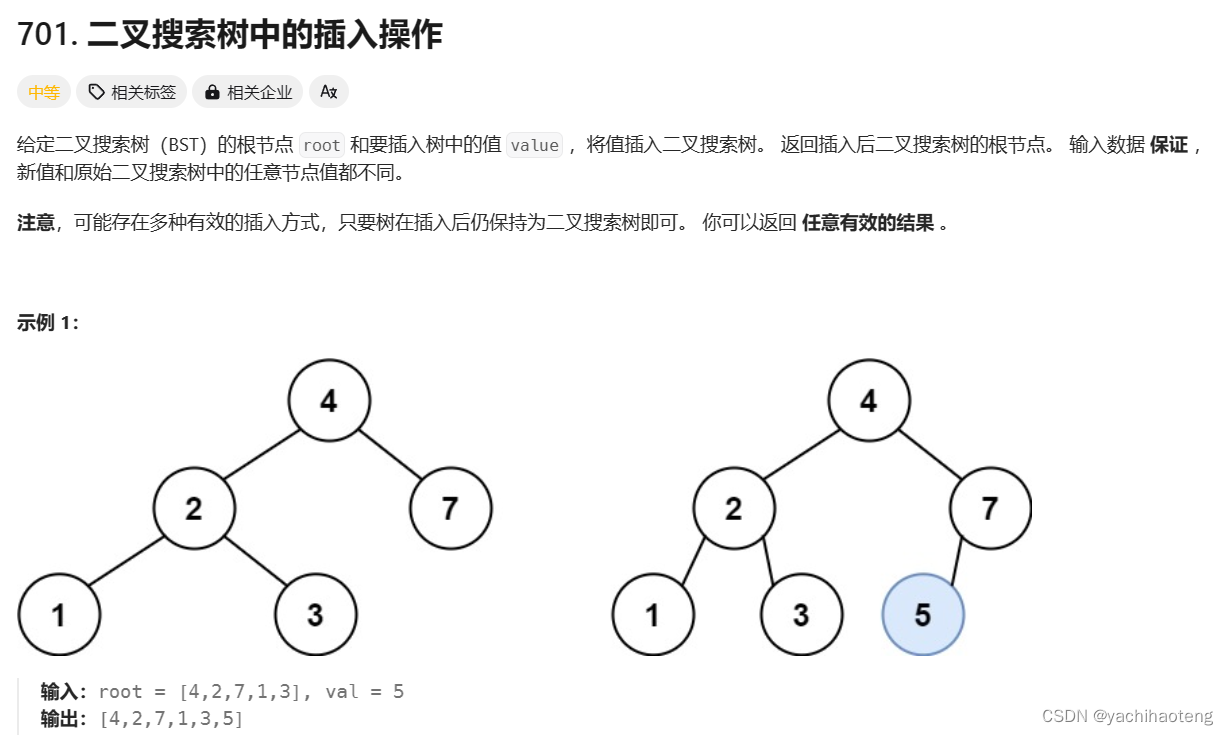
學習:對于二叉搜索樹來說只要插入的數據和原始二叉樹中的節點不同,則肯定能插入樹中并成為一個葉子節點。本題其實不用考慮題目中的改變樹的結構的插入方式。
代碼:遞歸法(本題需要插入節點并將更改后的樹層層返回)
//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {//確定終止條件if (root == nullptr) {TreeNode* node = new TreeNode(val);return node; //把新加入的節點進行返回}//確定單層遞歸邏輯if(root->val > val) {root->left = insertIntoBST(root->left, val); //把更改后的樹一層層往上返回}if(root->val < val) {root->right = insertIntoBST(root->right, val); //把更改后的樹一層層往上返回}return root;}
};450.刪除二叉搜索樹中的節點
文檔講解:代碼隨想錄刪除二叉搜索樹中的節點
視頻講解:手撕刪除二叉搜索樹中的節點
題目:?
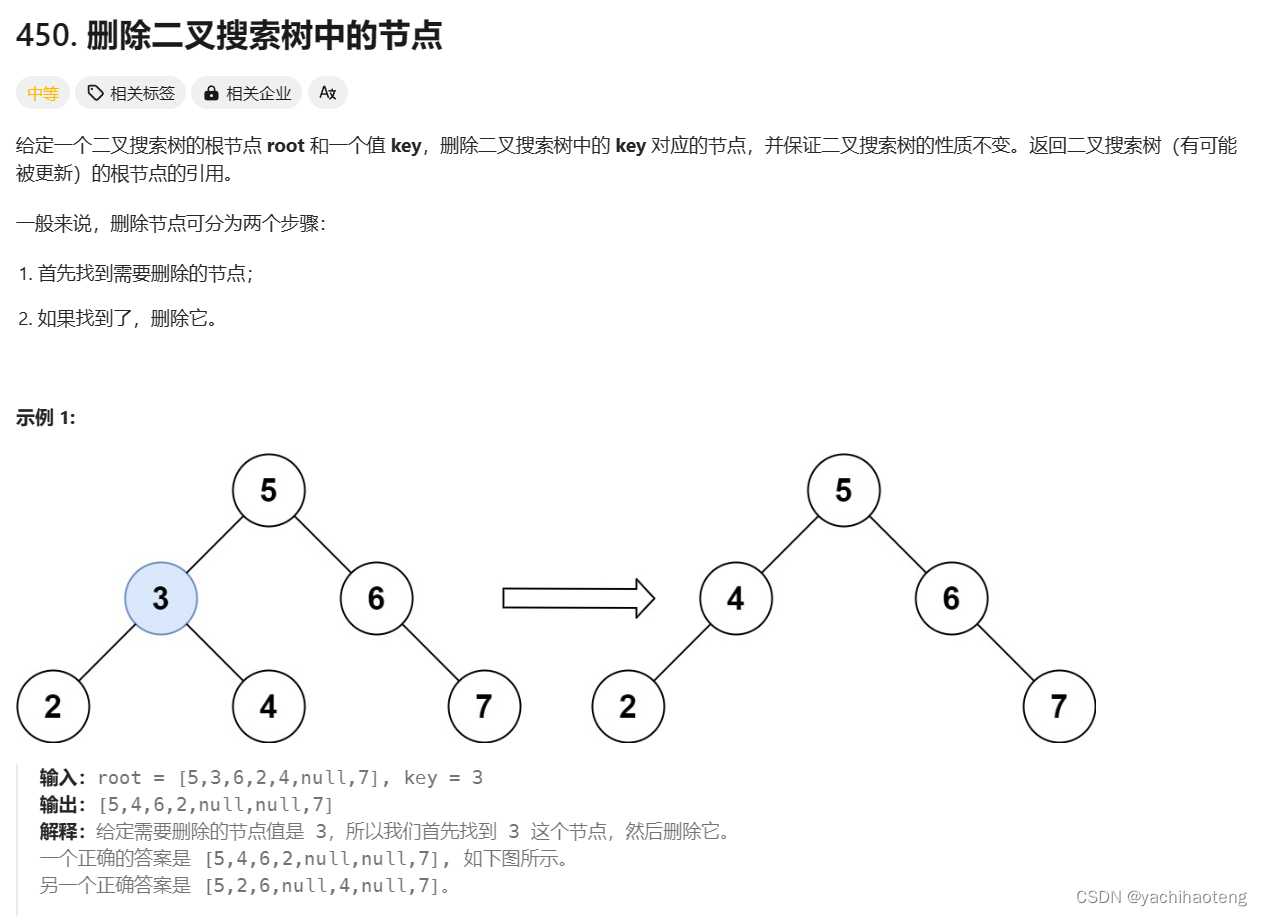
學習:
本題需要刪除二叉搜索樹的節點,我們首先要分析的是,刪除的情況有哪些:
- 要刪除的節點在二叉樹中不存在,二叉樹不需要修改。
- 要刪除的是葉子節點,那直接刪除葉子節點,返回nullptr即可。
- 要刪除的是中間節點,但中間節點左孩子為空,右孩子不為空,讓右孩子替代刪除節點。
- 要刪除的是中間節點,但中間節點右孩子為空,左孩子不為空,讓左孩子替代刪除節點。
- 要刪除的節點中左右孩子都不為空,則可以將刪除節點的左子樹的頭節點(左孩子)放到刪除節點的右子樹的最左面節點的左孩子上,返回刪除節點右孩子為新的根節點。(補充一種我采取的方式,使用刪除節點的后繼或者前序來替代刪除節點,但處理會復雜一些)
第5中情況動畫說明:
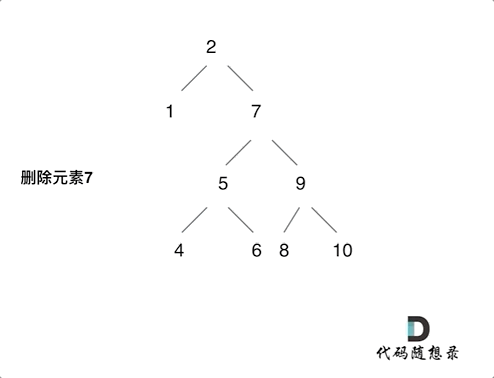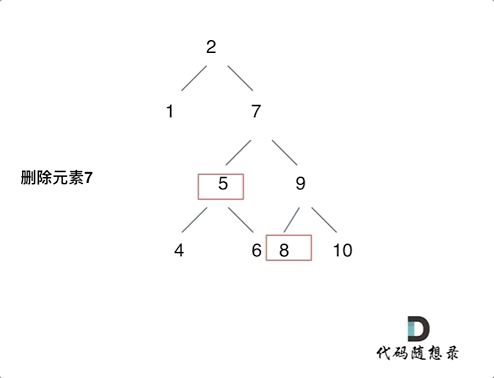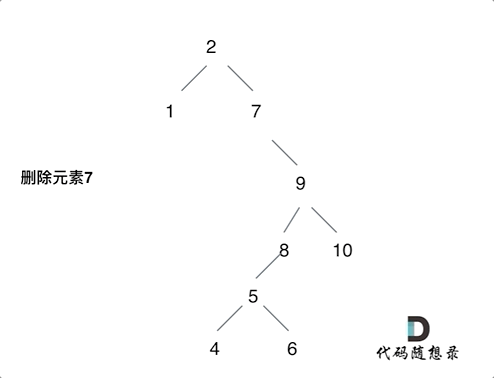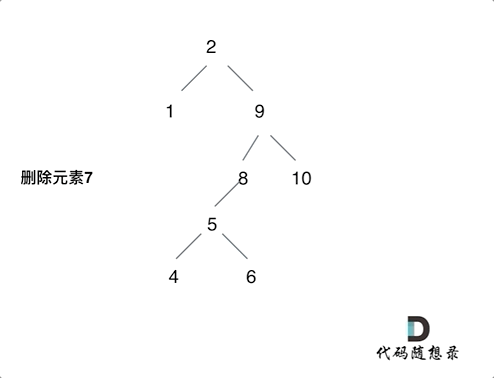
代碼:遞歸法
//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一種情況:沒找到刪除的節點,遍歷到空節點直接返回了if (root->val == key) {// 第二種情況:左右孩子都為空(葉子節點),直接刪除節點, 返回NULL為根節點if (root->left == nullptr && root->right == nullptr) {///! 內存釋放delete root;return nullptr;}// 第三種情況:其左孩子為空,右孩子不為空,刪除節點,右孩子補位 ,返回右孩子為根節點else if (root->left == nullptr) {auto retNode = root->right;///! 內存釋放delete root;return retNode;}// 第四種情況:其右孩子為空,左孩子不為空,刪除節點,左孩子補位,返回左孩子為根節點else if (root->right == nullptr) {auto retNode = root->left;///! 內存釋放delete root;return retNode;}// 第五種情況:左右孩子節點都不為空,則將刪除節點的左子樹放到刪除節點的右子樹的最左面節點的左孩子的位置// 并返回刪除節點右孩子為新的根節點。else {TreeNode* cur = root->right; // 找右子樹最左面的節點while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要刪除的節點(root)左子樹放在cur的左孩子的位置TreeNode* tmp = root; // 把root節點保存一下,下面來刪除root = root->right; // 返回舊root的右孩子作為新rootdelete tmp; // 釋放節點內存(這里不寫也可以,但C++最好手動釋放一下吧)return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};代碼:遞歸法(使用后繼作為代替)
//時間復雜度O(n)
//空間復雜度O(n)
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {//確定終止條件//沒有找到的話if(root == nullptr) return root;//找到了的話,分為4種情況if(root->val == key) {//第一種情況,要刪除的是葉子節點,則直接返回空if(root->left == nullptr && root->right == nullptr) {//內存釋放delete root;return nullptr;}//第二種情況,要刪除的是中間節點,但是左子樹為空,使用右子樹節點替代else if(root->left == nullptr && root->right != nullptr) {TreeNode* tmp = root;root = root->right;delete tmp;return root;}//第三種情況,要刪除的是中間節點,但是右子樹為空,使用左子樹節點替代else if(root->left != nullptr && root->right == nullptr) {TreeNode* tmp = root;root = root->left;delete tmp;return root;}//第四種情況,要刪除的是中間節點,且左右子樹都不為空//使用前驅或者后繼節點替代else {//使用后繼節點替代,即右子樹的最左邊的節點。TreeNode* cur = root->right; TreeNode* pre = nullptr; //指向cur的前一個節點while(cur->left != nullptr ) {pre = cur;cur = cur->left;}if(pre == nullptr) { //說明一次循環沒有進行,刪除節點的右子樹的根節點沒有左邊部分,則其自身就是刪除節點的后繼cur->left = root->left; //把刪除節點的左子樹保留delete root;return cur;}else { //說明至少進入了循環一次pre->left = cur->right; //先把cur分理出,并保存cur的右子樹(可能為空)cur->left = root->left; //將刪除節點的左右子樹釋放cur->right = root->right;delete root;return cur;}}}root->left = deleteNode(root->left, key);root->right = deleteNode(root->right, key);return root;}
};拓展:普通二叉樹的刪除方式?
學習:對于普通二叉樹的節點刪除來說,可以通過和葉子節點交換值得方式,然后再進行刪除。
代碼中目標節點(要刪除的節點)被操作了兩次:第一次是和目標節點的右子樹最左面節點交換。第二次直接被NULL覆蓋了。
代碼:
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root;if (root->val == key) {if (root->right == nullptr) { // 這里第二次操作目標值:最終刪除的作用return root->left;}TreeNode *cur = root->right;while (cur->left) {cur = cur->left;}swap(root->val, cur->val); // 這里第一次操作目標值:交換目標值其右子樹最左面節點。}root->left = deleteNode(root->left, key);root->right = deleteNode(root->right, key);return root;}
};總結
二叉搜索樹的特點要牢記,利用好二叉樹的特點能夠更有效的進行算法設計。
浮游菌檢測標準操作規程及GB/T 16292-2010測試方法解讀)





:Qt應用界面設計原則)



】運行配置找不到導入的自定義 makefile 項目)
)

)



應用程序)

(高級進階))