C++數據結構—

前言：本篇文章將繼續進行C++數據結構的講解——哈希表。

一.哈希表概念

二.哈希函數

1.除留取余法

三.哈希沖突

1.閉散列

線性探測

?（1）插入

（2）刪除

?2.?開散列

開散列概念

四.閉散列哈希表

1.基本框架?

2.插入

3.尋找

4.刪除

5.數據類型問題

五.開散列哈希表

1.基本框架

2.插入

3.尋找

4.刪除

總結

一.哈希表概念

順序結構以及平衡樹中，元素關鍵碼與其存儲位置之間沒有對應的關系，因此在查找一個元素時，必須要經過關鍵碼的多次比較。順序查找時間復雜度為O(N)，平衡樹中為樹的高度，即O(log_2 N)，搜索的效率取決于搜索過程中元素的比較次數。
理想的搜索方法：可以不經過任何比較，一次直接從表中得到要搜索的元素。
如果構造一種存儲結構，通過某種函數(hashFunc)使元素的存儲位置與它的關鍵碼之間能夠建立一一映射的關系，那么在查找時通過該函數可以很快找到該元素。

比如說：要統計一個全是小寫英文字母的字符串中各個英文字母出現的個數，該怎么做？？？

很容易，因為小寫英文字母有26個，所以我們直接創建一個大小為26的int數組并將值全部初始化為0，讓數組的每一位都代表一個小寫英文字母，該字母每出現一次，就讓該怎么對于位置的值++，最終每個位置的值便是對應小寫英文字母的個數。

該方式即為哈希(散列)方法，哈希方法中使用的轉換函數稱為哈希(散列)函數，構造出來的結構稱為哈希表(Hash Table)(或者稱散列表)?。

二.哈希函數

有時候我們可能不能像上邊一樣有多少種數據就創建多大的哈希表，比如說雖然我們只有1，12,103,1004,10005四個數要統計個數，難道要創建一個10005大小的數組嗎？？？?

1.除留取余法

實際上只需要創建大小為6的數組即可，此時我們可以使用哈希函數：除留取余法。

找到一個合適的除數，能夠讓上述數字取余之后分別為不同的值，從而拉進各個數字之間的距離，創建更小的哈希表。

比如說讓上述數字均取余上10，得到的就會是1,2,3,4,5，剛好對應數組各個位置。

三.哈希沖突

雖然上述函數可以解決大部分問題，但不妨有些時候會出現像1,11,111,1111這樣的數字，它們%10之后得到的數字均為1，這樣就會導致不同的值映射到相同的位置，從而導致哈希沖突。

?那么為了解決哈希沖突，有兩種常用的方法：閉散列和開散列。

1.閉散列

閉散列：也叫開放定址法，當發生哈希沖突時，如果哈希表未被裝滿，說明在哈希表中必然還有空位置，那么可以把key存放到沖突位置中的“下一個” 空位置中去。那如何尋找下一個空位置呢？

線性探測

線性探測：從發生沖突的位置開始，依次向后探測，直到尋找到下一個空位置為止。?

?（1）插入

通過哈希函數獲取待插入元素在哈希表中的位置。

如果該位置中沒有元素則直接插入新元素，如果該位置中有元素發生哈希沖突，使用線性探測找到下一個空位置，插入新元素。

（2）刪除

采用閉散列處理哈希沖突時，不能隨便物理刪除哈希表中已有的元素，若直接刪除元素會影響其他元素的搜索。比如刪除元素4，如果直接刪除掉，44查找起來可能會受影響。因此線性探測采用標記的偽刪除法來刪除一個元素。

哈希表的每個空間都給上一個標記
EMPTY此位置空， EXIST此位置已經有元素， DELETE元素已經刪除，通過枚舉實現：
enum State{EMPTY, EXIST, DELETE};??

?2.?開散列

開散列概念

開散列法又叫鏈地址法(開鏈法)，首先對關鍵碼集合用散列函數計算散列地址，具有相同地址的關鍵碼歸于同一子集合，每一個子集合稱為一個桶，各個桶中的元素通過一個單鏈表鏈接起來，各鏈表的頭結點存儲在哈希表中。

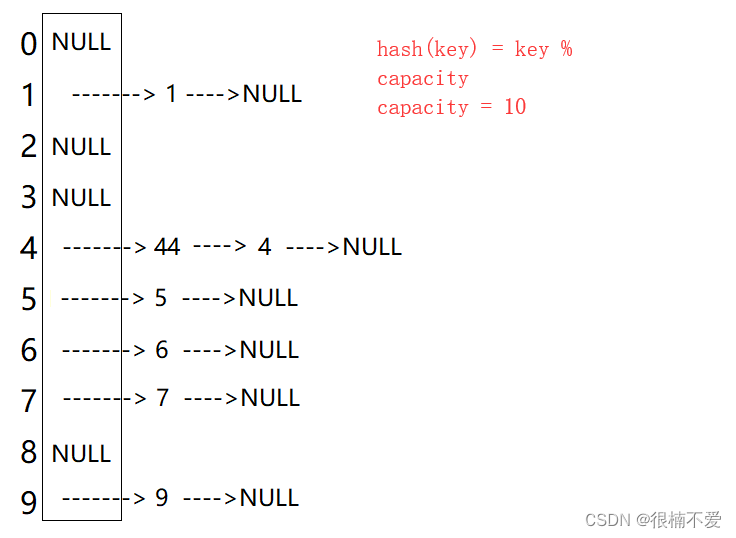
從上圖可以看出，開散列中每個桶中放的都是發生哈希沖突的元素。?由于其形狀很像一個桶，所以開散列哈希表又叫哈希桶。

四.閉散列哈希表

1.基本框架?

?下面來看代碼，我們先給出哈希表的基本框架：

namespace close_address
{enum State{EMPTY,EXIST,DELETE};template<class K,class V>struct HashData{pair<K, V> _kv;State _state = EMPTY;};template<class K, class V>class HashTable{public:private:vector<HashData<K, V>> _tables;size_t _n = 0;};
}

這里的_n用來記錄哈希表中數據的個數。?

2.插入

	bool Insert(const pair<K, V> kv){if (Find(kv.first))return false;size_t hashi = kv.first % _tables.size();//線性探測while (_tables[hashi]._state == EXIST){++hashi;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._state = EXIST;++_n;return true;}

插入步驟還是容易實現的，值得注意的是，哈希表也不允許相同數據存在，所以需要提前判斷，這里直接調用后邊的Find（）函數來判斷。

除此之外還有一個非常關鍵的點在于——擴容。

?因為雖然我們的哈希表是用vector作為底層，但是實際上填入數據時并一定是挨著存放的，所以我們需要在插入之前，提前創造空間。

?那么哈希表也要等數據存滿的時候才擴容嗎？？？并不是。

對于散列表，存在一個荷載因子的定義：

α = 填入表中的元素 / 散列表的長度

當表中的元素足夠多但并未滿時，此時如果繼續插入數據，發生哈希沖突的可能性就會極大，導致插入時間變長。所以這里我們規定，當荷載因子的值 >= 0.7時就進行擴容：

	HashTable(){_tables.resize(10);}

在擴容之前，應該給表一個初始的大小，這里通過構造函數使哈希表的初始長度為10。

		//擴容if (_n * 10 / _tables.size() >= 7){HashTable<K, V> newHT;newHT.tables.resize(_tables.size() * 2);for (size_t i = 0; i < _tables.size(); i++){if (_tables[i]._state == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);}

隨后進行擴容判斷，這里有一個細節，?因為荷載因子是一個浮點數，如果直接進行比較，我們還需進行類型轉換，所以我們直接讓哈希表數據個數乘10再來進行計算。

判斷成立則進行擴容，注意，哈希表的擴容并非像順序表那樣進行復制粘貼，因為哈希表擴容，代表著哈希函數的分母發生變化，所以其對應的取余后的下標位置也會發生變化。

這里我們通過新建一個二倍大小的哈希表，遍歷原表數據并在新表中調用插入函數進行插入，最后在通過交換即可。

3.尋找

	//尋找HashData<K, V>* Find(const K& key){size_t hashi = key % _tables.size();//線性探測while (_tables[hashi]._state == EXIST &&_tables[hashi]._state != EMPTY){if (_tables[hashi]._kv.first == key){return &_tables[hashi];}++hashi;hashi %= _tables.size();}return nullptr;}

尋找就比較簡單了， 通過要尋找的值計算出其在哈希表中的下標，判斷是否存在且是否為空，存在且不為空則進行判斷，相等返回，如果不相等，因為可能存在哈希沖突，所以循環往后遍歷，直至遇到空位置仍然沒有找到，說明其不在哈希表中，返回nullptr。

這里有一個細節，返回值為哈希表中對應位置的地址，這是為后邊的刪除做伏筆。

4.刪除

	//刪除bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret == nullptr){return false;}else{ret->_state = DELETE;--_n;return true;}}

刪除我們直接借用Find函數去找到對應位置，無需在通過哈希函數去尋找。

如果要刪除的元素不存在，則返回失敗，反之，將其位置的標記改為DELETE，即偽刪除。

下面來理解一下偽刪除：

因為我們在尋找和插入時的判斷條件均為標記位EMPTY，所以刪除時只需將該位置的標記改為DELETE，這樣就不會影響該位置對應的沖突位的尋找以及新的插入了。

5.數據類型問題

我們上述的哈希表實現能夠采用哈希函數進行取余操作的前提是數據為int類型，那如果是其他類型的數據，不能進行取余操作，又該如何使用哈希函數呢？？？

這里的方法是，通過建立仿函數，將其他類型轉換成int類型：

struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};

?此外，有一個特例，string類型不能直接轉換為int類型，所以想要滿足string類型，我們需要為其單獨創造一個仿函數：

struct HashStringFunc
{size_t operator()(const string& s){size_t hash = 0;for (auto e : s){hash += e;}return hash;}
};

思想為，將string類型的每個字符的ascll碼值加起來作為其int類型的數據。

隨后需要在模板中進行添加：

template<class K, class V,class Hash = HashFunc<K>>

這里采用了缺省參數，默認情況下為其他類型，當為string類型時，在傳入獨有的模版。?

五.開散列哈希表

1.基本框架

namespace hash_bucket
{template<class K,class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K,V>& kv):_kv(kv),_next(nullptr){}};template<class K,class V>class HashTable{typedef HashNode<K, V> Node;public:HashTable(){_tables.resize(10, nullptr);_n = 0;}private:vector<Node*> _tables;//指針數組size_t _n;};
}

不同于閉散列的哈希表vector中存放的是數據本身，哈希桶中vector存放的為節點指針。

2.插入

因為哈希桶可能會在一個位置下面插入很多的數據，如果采用尾插，就必須找到尾結點才能進行插入，效率會很低，所以我們采用頭插的方式：

		//插入bool Insert(const pair<K, V>& kv){//判斷是否存在if (Find(kv.first))return false;//擴容//......size_t hashi = kv.first % _tables.size();Node* newnode = new Node(kv);//頭插newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;}

創造一個新節點，讓新節點去指向原來的頭結點，再讓新節點成為頭結點。

下面我們來關注擴容問題，雖然哈希桶是通過鏈表的方式進行插入，原則上不用進行擴容就可以滿足所有數據的存放。但是如果數據過大，會導致每個桶中的數據量過于龐大，導致尋找操作的效率大大降低。所以規定，當數據個數等于哈希表的大小，即荷載因子α為1時，進行擴容。

那么哈希桶的擴容又該如何進行呢？？？

因為是節點的緣故，如果像閉散列那樣復用插入去擴容，那樣就等于同一個節點又創建了一份，而原節點最后還需要進行銷毀，這樣未免過于麻煩和浪費時間。

所以更好一點的做法是，新建立一個哈希桶，遍歷原桶的節點，讓其按照哈希函數去直接指向新桶，最后再將兩個桶進行交換：

			//擴容if (_n == _tables.size()){vector<Node*> newtables; (_tables.size() * 2, nullptr);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;size_t hashi = kv.first % newtables.size();cur->_next = newtables[hashi];newtables[hashi] = cur;cur = next;}_tables[i] = nullpter;}_tables.swap(newtables);}

3.尋找

		//尋找Node* Find(const K& key){size_t hashi = key % _tables.size();Node* cur = _tables[hashi];while (cur){if (cur->_kv.first == key)return cur;cur = cur->_next;}return nullptr;}

尋找操作較為簡單，就不在過多分享，注意返回值為節點類型。

4.刪除

鏈表的刪除無非就三種情況，刪除的是頭結點，或者是中間節點，尾結點。其中尾結點可以和中間節點共用一種方式。

那么如果刪除中間節點，就必須提前記錄該節點的前一個節點。

此外就是頭結點，提前定義一個prev，并置空，如果cur不為頭結點，就讓prev繼承cur，cur在往后，所以如果首次循環prev就為空，說明要刪除的節點即為頭結點。?

		bool Erase(const K& key){size_t hashi = key % _tables.size();Node* cur = _tables[hashi];Node* prev = nullptr;while (cur){if (cur->_kv.first == key){//刪除的是第一個節點if (prev == nullptr){_tables[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;}else{prev = cur;cur = cur->_next;}}return false;}

最后我們仍需使用仿函數來解決數據類型的問題，因方法與閉散列完全相同，這里不再重復。