- Distributed Sampling-Based Model Predictive Control via Belief Propagation for Multi-Robot Formation Navigation
- RAL 2024.4
- Chao Jiang 美國 University of Wyoming
預備知識
馬爾可夫隨機場(Markov Random Field, MRF)
馬爾可夫隨機場(MRF)是用于建模多個隨機變量之間相互依賴關系的概率圖模型。具有以下特點:
- MRF通過無向圖表示,節點代表隨機變量,邊表示變量之間的相互依賴關系。
- 每個節點的條件分布僅依賴于其鄰居節點,而不依賴于其他節點。
- 其核心思想是通過局部相互作用來捕捉全局行為。
信念傳播(Belief Propagation, BP)
信念傳播是一種在圖模型(如MRF)上進行推斷的算法。它可以用于計算邊緣概率分布或最大后驗概率估計。主要有兩種形式:
- 標準(BP):適用于樹結構或無環圖。在這些圖中,BP可以精確地計算邊緣概率分布。
- 循環(Loopy BP):適用于包含環的圖。雖然在有環的圖中BP不一定收斂或給出精確解,但在實踐中它常常表現良好,能提供近似解。
步驟:
- 初始化:將每個節點的初始信念設置為其先驗概率。
- 節點之間交換消息,包括關于一個節點的信念如何影響另一個節點。
- 邊緣概率計算:通過聚合消息計算每個節點的邊緣概率。
Q1 Background:本文試圖解決一個什么樣的問題?
- 具有復雜系統動力學和不確定性模型的隨機最優控制問題
- 多機器人最優軌跡優化問題
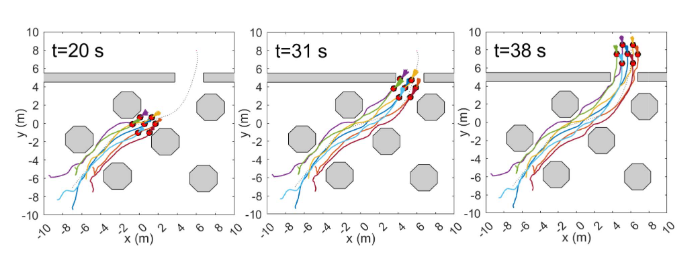
👉20x20的帶有靜態障礙物的方形環境。輪式機器人數量N=7。初始位置均勻隨機分布在左下角的5×5m區域,初始航向從[0,2π)采樣。
👉編隊目標:使6個機器人將自己定位成正六邊形,1個機器人位于編隊中心。每個機器人與其最近鄰居的距離為1.2m。最大通信范圍dmax=1.5 m,最小機器人間距離dmin=0.6 m。最大控制vmax=1.2 m/s。
Q2 What’s Known:之前解決這個問題有哪些方法?
- 基于優化的方法:動態規劃 | SCP | MPC
- 缺點:依賴梯度,需要計算導數,不太適合非光滑動力學或成本函數。隨著函數的復雜性(例如,非凸性、局部極小值)的增加,這些方法可能變得低效,甚至無法找到可行解。使用基于梯度的優化的現有MPC方法在平滑優化問題中大多是成功的。
- 基于采樣的方法:路徑積分控制 | 交叉熵 | 信息論MPC | 變分推理MPC
- 定義:使用由前向預測或模擬產生的隨機軌跡樣本來實現最優控制。
- 優點:不依賴于模型的精確梯度的計算,接受更通用的動力學。隨機前向搜索提供了一種解釋不確定性的原則性方法,使算法不太容易出現局部極小值。
Q3 What’s New:本文是用什么樣的方法如何解決這個問題的?
👉基于分布式采樣的MPC算法:將多機器人最優控制公式化為圖形模型上的概率推理(probabilistic inference over graphical model),并利用信念傳播(leverages belief propagation通過分布式計算實現推理。可以產生基于采樣的隨機優化的各種分布式最優控制算法。
👉具體Method如下:
建模
-
Model:經典的輪式機器人 - 兩輪驅動非完整Robot
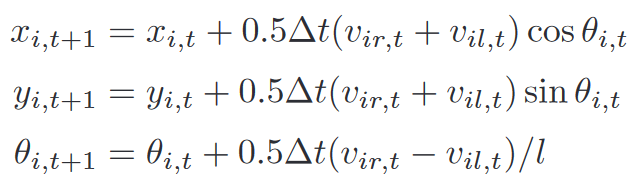
x x x, y y y是2D位置, θ \theta θ是航向角, v l v_l vl?和 v r v_r vr?代表左輪輸入速度和右輪輸入速度, l l l是左右輪距離 -
Proximity Graph
無向圖,如果 i i i 和 j j j 的歐幾里得距離 ≤ d m a x d_{max} dmax?(通信范圍限制),則 i i i, j j j存在邊,且它們倆互為鄰居。
所以邊集是時變的: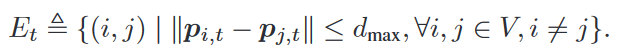
-
避碰和避障
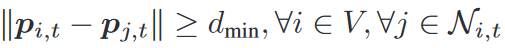
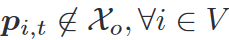
X o \mathcal{X}_o Xo?是障礙物占用的位置(膨脹后) -
導航和編隊保護
保持編隊移動到目標位置,同時避碰
即跟蹤參考軌跡 ∥ x i , t ? x r , t ∥ , ? t ∈ [ 0 , T ] \|x_{i,t}-x_{r,t}\|,\forall t\in[0,T] ∥xi,t??xr,t?∥,?t∈[0,T],參考軌跡 x r , t x_{r,t} xr,t? 通過全局運動規劃器獲得(環境圖全局給定),編隊由相對位置 Δ p i j \Delta p_{ij} Δpij?確定,當所需編隊保持不變時,以下等式成立:
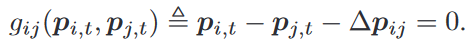
-
MPC軌跡優化問題
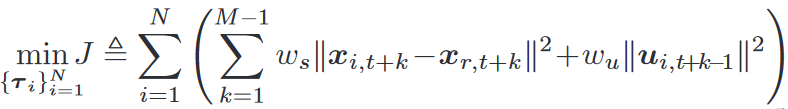
τ i ? { x i , t + k , u i , t + k } k = 0 M ? 1 \tau_i\triangleq\{x_{i,t+k},u_{i,t+k}\}_{k=0}^{M-1} τi??{xi,t+k?,ui,t+k?}k=0M?1?是狀態控制序列, N N N是智能體數量, M M M是控制時域
key:使用什么樣的方法求解這個MPC軌跡優化問題
推理問題
- 目標:找到最優軌跡上的概率分布,從而找到每個機器人的最優控制。
- 概述:首先將多機器人團隊建模為一個馬爾可夫隨機場(MRF)的概率圖形模型,然后通過局部消息傳遞將信念傳播(BP)用于分布式推理。最后,開發了一種基于采樣的MPC算法來獲得每個機器人的最優控制。
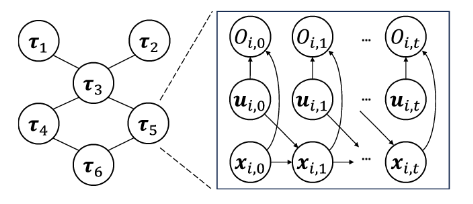
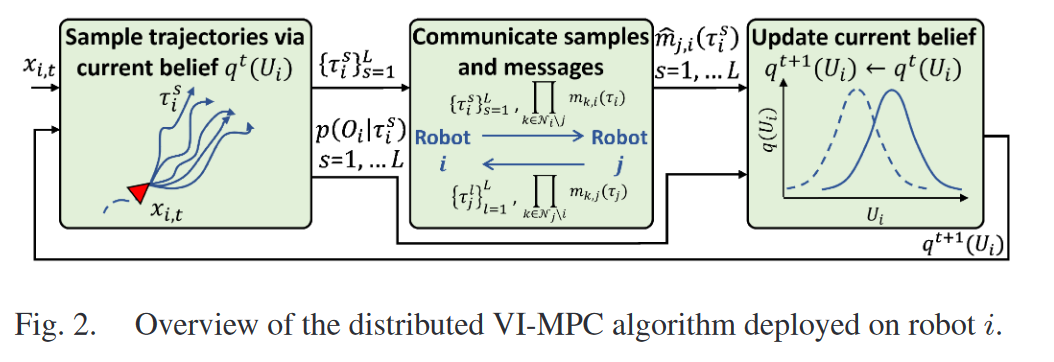
- 采樣軌跡
輸入: t t t時刻狀態 x x x和當前的置信分布 q ( U ) q(U) q(U)
根據 q ( U ) q(U) q(U)對軌跡 τ \tau τ進行采樣,得到 L L L個樣本
計算每個樣本軌跡的觀測似然 p ( O ∣ τ ) p(O|\tau) p(O∣τ)- 傳遞樣本軌跡和消息
i i i 發送軌跡樣本給鄰居 j j j,并接受鄰居 j j j的軌跡樣本
i i i 計算并傳遞消息 m k , i ( τ ) m_{k,i}(\tau) mk,i?(τ)( i i i除了 j j j外的所有鄰居 k k k對軌跡 τ i \tau_i τi?的估計
i i i 接受 j j j 計算的消息( j j j除了 i i i外的所有鄰居 k k k對軌跡 τ j \tau_j τj?的估計- 更新當前置信分布
根據收到的所有鄰居機器人的消息和當前時刻的觀測信息更新當前的置信分布 q ( U ) q(U) q(U)

Q4 What’s the Contribution:本文還有什么其他的貢獻嗎?
- 主要貢獻是完全分布式框架,每個機器人只需要局部信息。它將基于采樣的優化方法[6]、[7]、[8]、[9]、[10]擴展到多機器人問題。
- 對比CMPC,計算速度快
- 對比基于ADMM求解的MPC,計算速度快且成功率高(分別為82%和98%)
Q5 What’s the Inspiration
- 模型比較常規,文章重點在于怎么求解問題,把基于采用的隨機最優控制(變分推理)用到了求解DMPC問題中,核心思想還是每個機器人根據其他機器人的信息和自己的觀測不斷調整和優化自身的軌跡,達到全局最優的控制目標。
- 求解都比較數學,MRF和BP的地方沒太看懂,這部分對我的工作沒太大用處,但如果有人能看懂這個數學部分把他做到無人機再加個真機實驗應該能寫個好文章

)








)

![[數據集][目標檢測]彈簧上料檢測數據集VOC+YOLO格式142張2類別](http://pic.xiahunao.cn/[數據集][目標檢測]彈簧上料檢測數據集VOC+YOLO格式142張2類別)






—測試模型)