大跟堆介紹

大根堆（Max Heap）是一種特殊的二叉樹結構，它滿足以下兩個條件：
1.完全二叉樹：大根堆是一棵完全二叉樹，即除了最后一層外，其余每一層的節點都是滿的，最后一層的節點都集中在最左邊。
2.堆性質：每個節點的值都大于或等于其子節點的值。
大根堆的典型操作包括插入，獲取root節點的最大值。

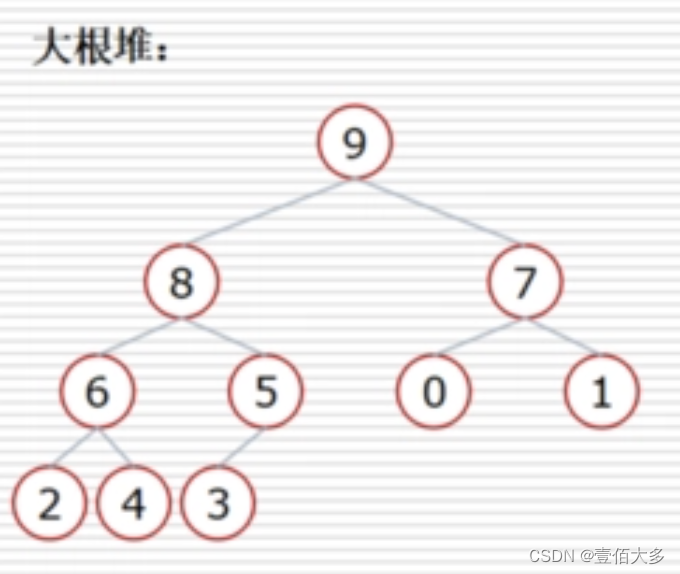
大跟堆的結構

大根堆的結構
大根堆可以用數組來表示，因為它是一棵完全二叉樹。對于一個存儲在數組中的大根堆：
根節點的索引為 0。
給定一個節點的索引位置i：
父節點的索引為 (i - 1) / 2。
左子節點的索引為 2 * i + 1。
右子節點的索引為 2 * i + 2。

大跟堆的應用場景

大根堆（Max Heap）在許多算法和應用中都有重要的作用，特別是在需要頻繁訪問最大元素的場景中。以下是一些常見的應用場景：

1. 優先隊列
   優先隊列是一種特殊的隊列，每次出隊的元素都是隊列中優先級最高的元素。大根堆可以用來實現優先隊列，其中堆頂元素始終是優先級最高的元素。
   應用舉例：
   操作系統的任務調度：調度器選擇優先級最高的任務進行執行。
   網絡數據包處理：路由器處理優先級最高的數據包。
2. 堆排序
   堆排序是一種利用堆數據結構設計的排序算法。其基本思想是將待排序序列構建成一個大根堆，此時整個序列的最大值即為堆頂元素。將堆頂元素移出堆（與堆的最后一個元素交換），然后對剩余元素重新構建堆，反復執行上述操作，直到所有元素有序。
   應用舉例：
   大數據集的排序：在需要對大量數據進行排序時，堆排序的空間效率較高。
3. 動態數據流中的最大值
   在處理動態數據流時，使用大根堆可以實時維護當前數據流中的最大值。
   應用舉例：
   股票交易系統：實時維護當前交易中的最大交易量。
   傳感器數據監控：實時監控傳感器數據流中的最大值。
4. 找到第 K 大的元素
   在一個無序數組中查找第 K 大的元素，可以使用大根堆來實現。首先構建一個包含數組中前 K 個元素的大根堆，然后遍歷數組剩余元素，如果當前元素小于堆頂元素，則替換堆頂元素并調整堆，最終堆頂元素即為第 K 大的元素。
   應用舉例：
   排名系統：在一組分數中找到第 K 高的分數。
   數據分析：在一組數據中找到第 K 大的數據點。
5. 合并多個有序序列
   在合并多個有序序列時，可以使用大根堆來保持當前最小元素的順序。將每個序列的首元素插入大根堆，然后每次取出堆頂元素并插入其所在序列的下一個元素，直到所有元素都被處理完畢。
   應用舉例：
   外部排序：當數據量大到無法全部放入內存時，可以先將數據分塊排序，然后合并多個有序塊。
   多路歸并排序：將多個有序的輸入流合并為一個有序的輸出流。
6. 圖的最短路徑算法（如 Dijkstra 算法）
   在 Dijkstra 算法中，需要使用優先隊列來選擇當前未訪問節點中距離起點最近的節點。大根堆可以用來實現這個優先隊列，以保證每次都能高效地選擇最短路徑的下一步節點。
   應用舉例：
   地圖導航系統：計算從一個地點到另一個地點的最短路徑。
   網絡路由優化：尋找數據包在網絡中傳輸的最優路徑。
7. 事件驅動模擬
   在事件驅動的模擬系統中，需要按照事件的發生時間順序來處理事件。使用大根堆可以有效地管理和調度這些事件。
   應用舉例：
   離散事件模擬：如模擬交通流、制造過程等。
   計算機圖形學：處理動畫中事件的時間調度。

大跟堆的代碼實現

插入操作：
插入新元素時，將元素添加到數組的末尾（完全二叉樹的最后一個位置），然后進行“上浮”操作（也稱為堆化）以恢復堆的性質。
上浮操作：
將新元素與其父節點比較，如果大于父節點，則交換位置，繼續向上比較，直到元素小于或等于父節點，或者到達根節點。

public void insert(int key) {if (size == capacity) {throw new RuntimeException("Heap is full");}heap[size] = key; // 將新元素放在堆尾int current = size;size++;// 上浮操作while (current != 0 && heap[parent(current)] < heap[current]) {swap(parent(current), current);current = parent(current);}
}

2.刪除最大值操作：
刪除最大值（根節點）時，將數組的最后一個元素移動到根節點位置，然后進行“下沉”操作（也稱為堆化）以恢復堆的性質。
下沉操作：
將根節點與其左右子節點比較，如果小于其中一個子節點，則與較大的子節點交換位置，繼續向下比較，直到元素大于或等于子節點，或者到達葉節點。

public int extractMax() {if (size <= 0) {throw new RuntimeException("Heap is empty");}int root = heap[0]; // 保存根節點heap[0] = heap[size - 1]; // 將最后一個元素移到根節點位置size--;// 下沉操作maxHeapify(0);return root;
}private void maxHeapify(int i) {int largest = i;int left = leftChild(i);int right = rightChild(i);if (left < size && heap[left] > heap[largest]) {largest = left;}if (right < size && heap[right] > heap[largest]) {largest = right;}if (largest != i) {swap(i, largest);maxHeapify(largest);}
}

3.交換元素：
在堆的操作過程中，經常需要交換兩個節點的位置。

private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;
}

4.完整的大根堆實現
以下是大根堆的完整實現，包括構造函數、插入操作、刪除最大值操作和輔助方法。

public class MaxHeap {private int[] heap;private int size;private int capacity;// 構造函數public MaxHeap(int capacity) {this.capacity = capacity;this.heap = new int[capacity];this.size = 0;}// 獲取父節點索引private int parent(int i) { return (i - 1) / 2; }// 獲取左子節點索引private int leftChild(int i) { return 2 * i + 1; }// 獲取右子節點索引private int rightChild(int i) { return 2 * i + 2; }// 插入新元素public void insert(int key) {if (size == capacity) {throw new RuntimeException("Heap is full");}heap[size] = key; // 將新元素放在堆尾int current = size;size++;// 上浮操作while (current != 0 && heap[parent(current)] < heap[current]) {swap(parent(current), current);current = parent(current);}}// 提取最大元素（根節點）public int extractMax() {if (size <= 0) {throw new RuntimeException("Heap is empty");}int root = heap[0]; // 保存根節點heap[0] = heap[size - 1]; // 將最后一個元素移到根節點位置size--;// 下沉操作maxHeapify(0);return root;}// 下沉操作private void maxHeapify(int i) {int largest = i;int left = leftChild(i);int right = rightChild(i);if (left < size && heap[left] > heap[largest]) {largest = left;}if (right < size && heap[right] > heap[largest]) {largest = right;}if (largest != i) {swap(i, largest);maxHeapify(largest);}}// 交換元素private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}// 主函數示例public static void main(String[] args) {MaxHeap maxHeap = new MaxHeap(10);maxHeap.insert(3);maxHeap.insert(1);maxHeap.insert(4);maxHeap.insert(1);maxHeap.insert(5);maxHeap.insert(9);maxHeap.insert(2);maxHeap.insert(6);maxHeap.insert(5);System.out.println("Extracted max: " + maxHeap.extractMax());System.out.println("Extracted max: " + maxHeap.extractMax());System.out.println("Extracted max: " + maxHeap.extractMax());}
}