用C語言把一棵普通二叉樹安排得明明白白

1. 樹的相關術語

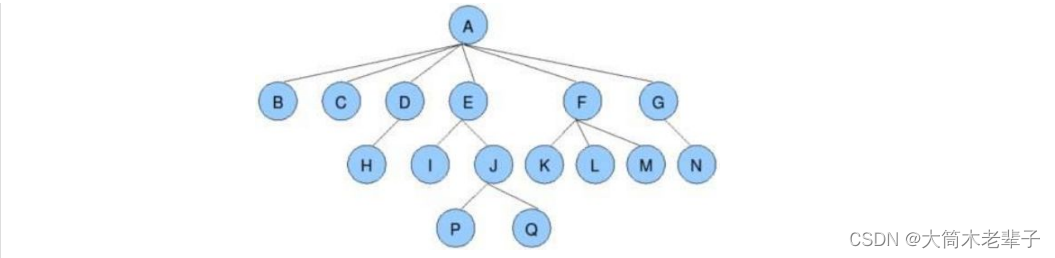
結點的度：一個結點含有的子樹的個數稱為該結點的度；如上圖：A的為6

葉結點或終端結點：度為0的結點稱為葉結點；如上圖：B、C、H、I...等結點為葉結點

非終端結點或分支結點：度不為0的結點；如上圖：D、E、F、G...等結點為分支結點

雙親結點或父結點：若一個結點含有子結點，則這個結點稱為其子結點的父結點；如上圖：A是B的父結點

孩子結點或子結點：一個結點含有的子樹的根結點稱為該結點的子結點；如上圖：B是A的孩子結點

兄弟結點：具有相同父結點的結點互稱為兄弟結點；如上圖：B、C是兄弟結點

樹的度：一棵樹中，最大的結點的度稱為樹的度；如上圖：樹的度為6

結點的層次：從根開始定義起，根為第1層，根的子結點為第2層，以此類推；

樹的高度或深度：樹中結點的最大層次；如上圖：樹的高度為4

堂兄弟結點：雙親在同一層的結點互為堂兄弟；如上圖：H、I互為兄弟結點

結點的祖先：從根到該結點所經分支上的所有結點；如上圖：A是所有結點的祖先

子孫：以某結點為根的子樹中任一結點都稱為該結點的子孫。如上圖：所有結點都是A的子孫

森林：由m（m>0）棵互不相交的樹的集合稱為森林；

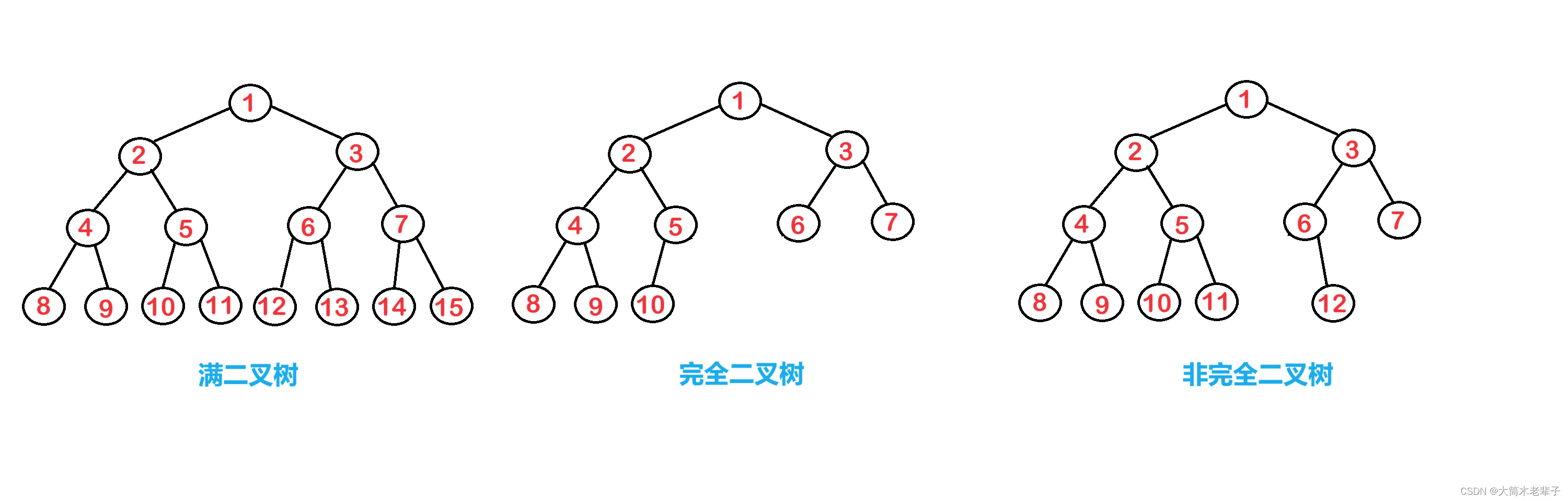
滿二叉樹：深度為k且有 $2^{k}-1$ 個結點的二叉樹。在滿二叉樹中，每層結點都是滿的，即每層結點都具有最大結點數。

滿二叉樹的順序表示：從二叉樹的根開始，按層間從上到下，層內從左到右的順序進行編號（0，1，2，……，n-1）。

完全二叉樹：深度為k，結點數為n的二叉樹，如果其結點0~n-1的位置序號分別與等高的滿二叉樹的結點1~n-1的位置序號一一對應，則為完全二叉樹。完全二叉樹的特點為：(1)葉子結點只可能出現在最后兩層；(2)度數為1的結點個數為0或1。

?2. 二叉樹的性質

性質1：在二叉樹的第i層上至多有 $2^{i-1}$ 個結點（i>=1）

性質2：深度為k的二叉樹至多有 $2^{k}-1$ 個結點(k>=1)

性質3：對任意一棵二叉樹T，若終端結點數為 $n_{1}$ ，而其度數為2的結點數為 $n_{2}$ ，則? ? ? ? ? ? ? ? ? ? ? ? ? ? ? $n_{1} = n_{2}+1$

性質4：具有n個結點的完全二叉樹的深度為 $(log_{2}n)+1$

性質5：對于具有n個結點的完全二叉樹，如果按照從上到下，從左到右的順序對完全二叉樹? ? ? ? ? ? ? ?中的所有結點從0開始編號，則對于任意序號為i的結點，其雙親結點的序號為? ? ? ? ? ? ? ? ? ? ? ? ?(i-1)/2，左孩子的序號為2*i+1，右孩子的序號為2*i+2。

證明略，但是上面的性質5在堆中有較為重要價值，在上一篇文章中有證明：全面詳解堆-CSDN博客?

1. 二叉樹的聲明以及要實現的接口

typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉樹銷毀
void BinaryTreeDestory(BTNode** root);
// 二叉樹節點個數
int BinaryTreeSize(BTNode* root);
// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root);
// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉樹前序遍歷 
void BinaryTreePrevOrder(BTNode* root);
// 二叉樹中序遍歷
void BinaryTreeInOrder(BTNode* root);
// 二叉樹后序遍歷
void BinaryTreePostOrder(BTNode* root);
// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root);
// 判斷二叉樹是否是完全二叉樹
int BinaryTreeComplete(BTNode* root);
//樹的高度
int TreeHeight(BTNode* root);

2. 通過前序遍歷數組構建二叉樹

在對二叉樹進行操作之前，我們需要有一棵二叉樹。

根據二叉樹的用途不同，在二叉樹中插入元素的方式繁多且復雜，在初學階段不需要太多的了解。

于是，我們可以采用暴力構建二叉樹的方式，也就是手動實現結點之間的相互鏈接關系：

BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

但是，按照這種方式來構建樹，每個不同的樹都需要我們編寫邏輯來實現，十分的麻煩。

由于包含空指針表示的前序遍歷序列與二叉樹之間存在著一一對應的關系，所以，我們可以采用將前序遍歷數組還原為樹的方式來構建樹（前序最好理解，中序后序調整子樹創建順序即可）：

// 通過前序遍歷的數組"ABD##E#H##CF##G##"構建二叉樹
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}else{BTNode* root = BuyNode(a[*pi]);(*pi)++;root->left = BinaryTreeCreate(a, n, pi);root->right = BinaryTreeCreate(a, n, pi);return root;}
}

a為存放前序遍歷序列的數組，'#'表示當前結點為空指針；

n表示數組a的元素個數；

pi為表示當前數組下標的變量的指針，初始值為0，每有一個元素加入到樹中，(*pi)++。

3. 二叉樹銷毀

?這里采用的是后序遍歷來釋放結點，否則需要定義變量來記錄左右子樹的根結點。

// 二叉樹銷毀
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL)return;else{BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL;}
}

4. 二叉樹的結點個數

利用遞歸即可解決，整棵樹的結點數 = 左子樹的結點數 + 根結點（1個）+ 右子樹的結點數。

同理，左右子樹也是相同的邏輯。

某棵子樹（某結點的左子樹或右子樹）為空時，返回0。

// 二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{if (root == NULL)return 0;return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

5. 二叉樹的葉子結點數

與上面的算法相似，但是此處我們只統計葉子結點數。

葉子結點區別于其他結點的特點是，其左右孩子都為空，如果當前結點符合條件我們就返回1，表示當前結點為葉子結點。

假如當前結點不是葉子結點，那么：

以當前結點為根的子樹的葉子結點數 = 左子樹葉子結點數 + 右子樹葉子結點數。

等式中不再包含根結點。

// 二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

6. 二叉樹第k層的結點數

同樣的遞歸思路，第k層結點數 = 左子樹第k-1層結點數 + 右子樹第k-1層結點數。

但是我們需要一個參數k來判斷當前結點位于第幾層，以及是否需要返回。

每深入一層，k就減1，當k等于1時返回1，表示已找到一個所求結點。

// 二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

7. 查找值為x的結點

如果當前結點的值為x，則直接返回當前結點。

否則，先到左子樹進行尋找，若左子樹沒有（返回值為NULL）就找右子樹。

// 二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* Find = BinaryTreeFind(root->left, x);if (Find == NULL){Find = BinaryTreeFind(root->right, x);}return Find;
}

8.二叉樹的遞歸與非遞歸遍歷

二叉樹的遞歸遍歷較為簡單，但是非遞歸算法卻十分復雜，需要用到棧來模擬遞歸進行實現。

在該文章中有詳細介紹：棧與遞歸的實現-CSDN博客

9. 樹的高度

樹的高度指樹中結點的最大層次。

所以樹的高度 = 左子樹與右子樹中較高者的高度 + 1（根結點）。

//樹的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}

?10. 層序遍歷

層序遍歷也就是廣度優先遍歷，實現這個算法需要用到隊列的幫助。

由于C語言不支持隊列，所以在這里寫了一個簡易的隊列。

其中，Get函數會在獲取隊頭結點的同時將其出隊，這樣實現對于我們當前算法的實現來說，使用起來更加方便。

當然，下面這段代碼只是幫助理解，直接忽略也可，只要你知道我對隊列進行了什么操作。

typedef BTNode* QDataType;// 鏈式結構：表示隊列 
typedef struct QListNode
{struct QListNode* _next;QDataType _data;
}QNode;// 隊列的結構 
typedef struct Queue
{QNode* _front;QNode* _rear;int size;
}Queue;//初始化
void Inite(Queue* q)
{q->size = 0;q->_front = NULL;q->_rear = NULL;
}//入隊
void Push(Queue* q, QDataType x)
{QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->_data = x;newnode->_next = NULL;if (q->_rear == NULL){q->_front = q->_rear = newnode;}else{q->_rear->_next = newnode;q->_rear = newnode;}q->size++;
}//出隊
QDataType Get(Queue* q)
{if (q->size == 0)return NULL;QDataType temp = q->_front->_data;QNode* del = q->_front;if (q->size == 1){q->_rear = NULL;}q->_front = q->_front->_next;free(del);q->size--;return temp;
}//銷毀隊列
void DestroyQueue(Queue* q)
{QDataType temp;while (q->_front){temp = Get(q);}
}

基本思路就是：

1. 出隊得到一個結點并訪問。

2. 如果當前結點有孩子，則將其孩子全部入隊。

3. 不斷重復以上兩步，知道隊中無結點。

// 層序遍歷
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;Inite(&q);Push(&q, root);BTNode* cur = NULL;while (cur = Get(&q)){printf("%c ", cur->data);if(cur->left != NULL)Push(&q, cur->left);if(cur->right != NULL)Push(&q, cur->right);}DestroyQueue(&q);
}

?11. 判斷二叉樹是否是完全二叉樹

根據完全二叉樹的特點，我們總結出以下判斷標準：

1. 如果某個結點只有右孩子而沒有左孩子，則該樹一定不是完全二叉樹。

2. 如果某個結點不是滿的（缺少左孩子或右孩子），則位置序號在其之后的結點一定既沒有? ? ? 左孩子，又沒有右孩子，否則就是非完全二叉樹。

// 判斷二叉樹是否是完全二叉樹
int BinaryTreeComplete(BTNode* root)
{Queue q;Inite(&q);Push(&q, root);BTNode* cur = NULL;do{cur = Get(&q);if (cur->left == NULL && cur->right != NULL)return 0;else if(cur->left != NULL && cur->right != NULL){Push(&q, cur->left);Push(&q, cur->right);}} while (cur->right);while (q.size != 0){cur = Get(&q);if (cur->left != NULL || cur->right != NULL)return 0;}return 1;DestroyQueue(&q);
}

12. oj練習

12.1 單值二叉樹. - 力扣（LeetCode）

第一種思路：保存根結點的值，然后用其與所有結點進行比較。

bool judge(struct TreeNode* root, int com)
{if(root == NULL)return true;if(root->val != com)return false;return judge(root->left, com) && judge(root->right, com);
}bool isUnivalTree(struct TreeNode* root) {int com = root->val;return judge(root, com);
}

為了提高代算法的效率，也可以將com變量改為全局變量。

第二種思路：我們找到題目要求的一個等價條件——除了葉子結點，所有結點的值都與自己孩子的值相等。

bool isUnivalTree(struct TreeNode* root) {if(root == NULL)return true;if(root->left && root->left->val != root->val || root->right && root->right->val != root->val)return false;return isUnivalTree(root->left) && isUnivalTree(root->right);
}

12.2 相同的樹. - 力扣（LeetCode）

采用遞歸的思路，兩棵樹相同意味著他們：根結點相同，左子樹相同，右子樹相同。

左右子樹相同，包括左右子樹都為空的情況。

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL || p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

12.3 對稱的樹. - 力扣（LeetCode）

觀察示例可以發現，這道題可以采用與上道題如出一轍的思路，只不過我們要比較的兩棵樹是根結點的左右子樹。

同時，比較的邏輯也需要更改，左子樹的右孩子應該與右子樹的左孩子比較，左子樹的左孩子應該與右孩子的右子樹比較。

bool judge(struct TreeNode* root1, struct TreeNode* root2)
{if(root1 == NULL && root2 == NULL)return true;if(root1 == NULL || root2 == NULL || root1->val != root2->val)return false;return judge(root1->left, root2->right) && judge(root1->right, root2->left);
}bool isSymmetric(struct TreeNode* root) {return judge(root->left, root->right);
}

12.4 另一棵樹的子樹. - 力扣（LeetCode）

這道題可以利用到“相同的樹”那道題的函數，我們只需要遍歷root，然后將其的子樹依次與subRoot進行比較即可。

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL || p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root == NULL)return false;if(isSameTree(root, subRoot))return true;return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

12.5 二叉樹的前序遍歷. - 力扣（LeetCode）

?這道題并不是簡單地對二叉樹進行前序遍歷，而是要求我們返回存儲前序遍歷序列的數組。

首先需要動態開辟一個存儲結果的數組，但問題是開辟多少合適呢？

當然，在這道題中我們可以直接開辟100個空間的數組。

假如我們不知道這么一個條件呢？

可以用動態的順序表來管理，但鑒于需要我們自己實現，似乎就有點麻煩。

這時，我們就可以用到上面的BinaryTreeSize函數了，先求出樹中的結點個數，再進行我們接下來的操作。

與利用前序遍歷數組構建二叉樹相同，我們這里也需要一個pi來指示數組當前的下標。

下面的這段代碼中，直接用returnSize來充當了這個pi。

int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}void pretraversal(struct TreeNode* root, int* arr, int* pi)
{if(root == NULL)return;arr[*pi] = root->val;(*pi)++;pretraversal(root->left, arr, pi);pretraversal(root->right, arr, pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize) {int* arr = (int*)malloc(sizeof(arr) * TreeSize(root));*returnSize = 0;pretraversal(root, arr, returnSize);return arr;
}