算法學習筆記（5.0）-基于比較的高效排序算法-歸并排序

##時間復雜度O(nlogn)

##遞歸實現歸并排序

##原理

##圖例

##代碼實現

##非遞歸實現歸并排序

##釋

#代碼實現

##遞歸實現歸并排序

##原理

是一種基于分治策略的基礎排序算法。

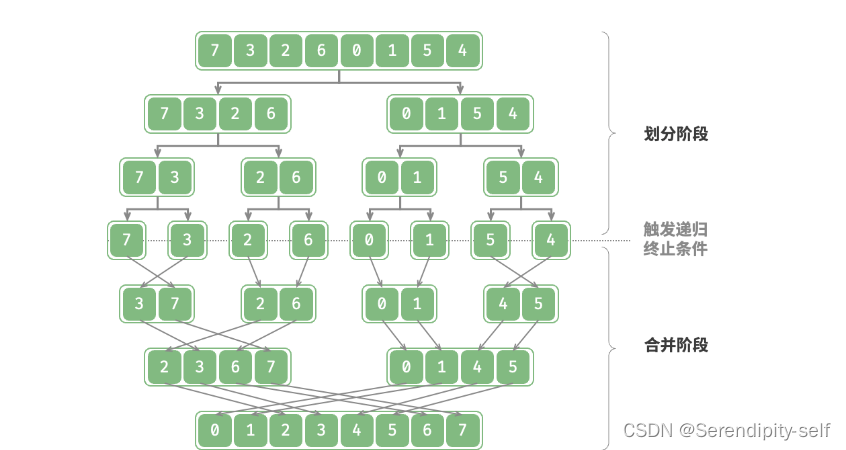
1.劃分階段：通過不斷遞歸地將數組從中點處分開，將長數組的排序問題轉化成段數組的排序問題。

2.合并階段：當子數組的長度為1時終止劃分，開始合并，持續不斷地將左右兩個較短的有序數組合并為一個較長的有序數組，直到結束。

##圖例

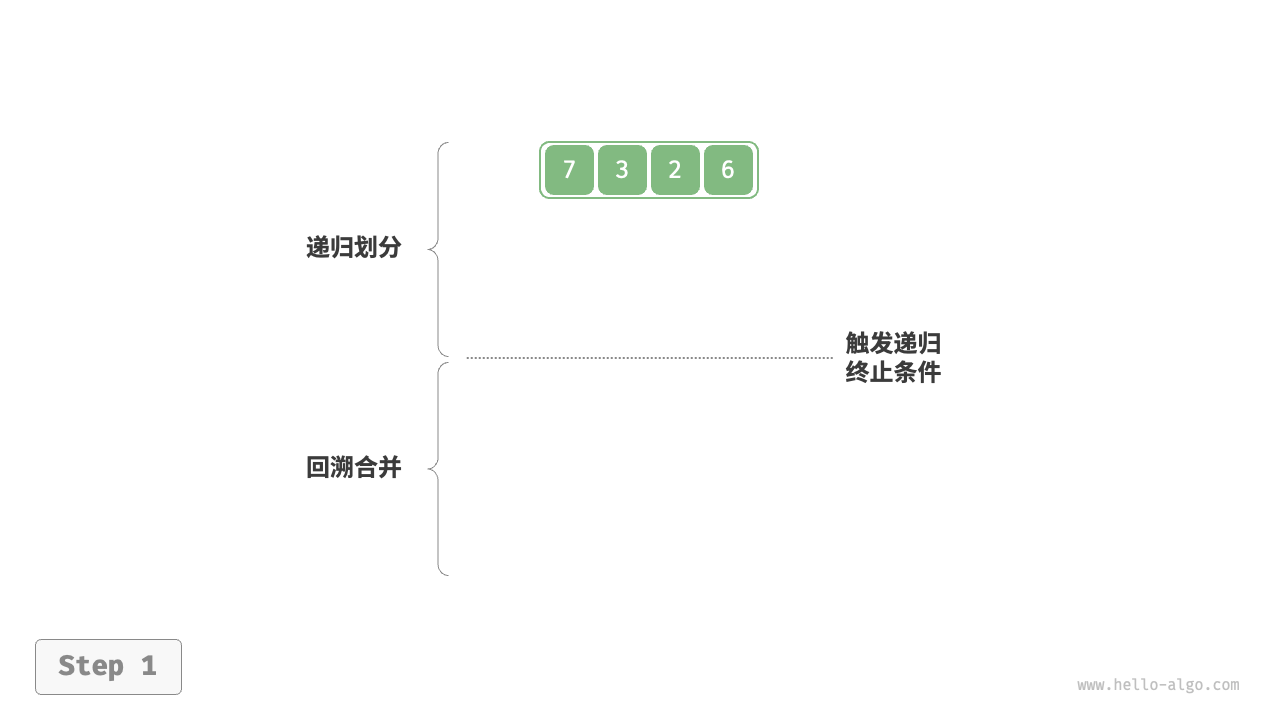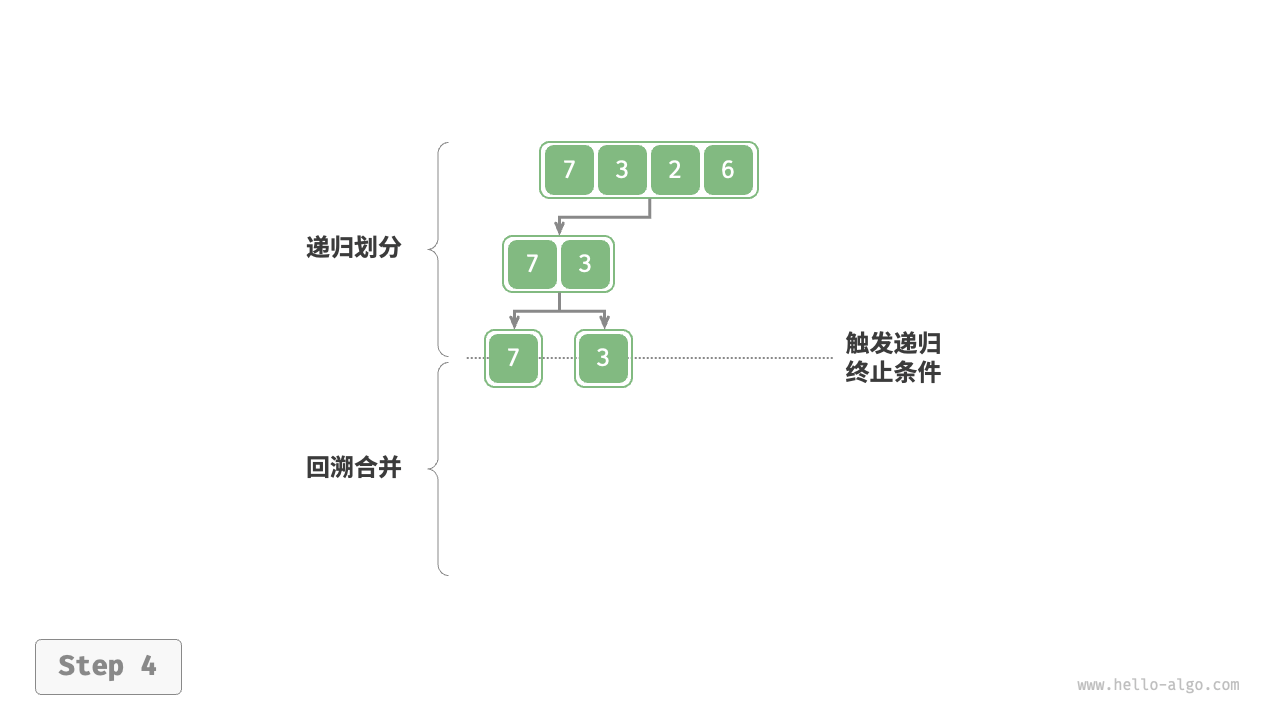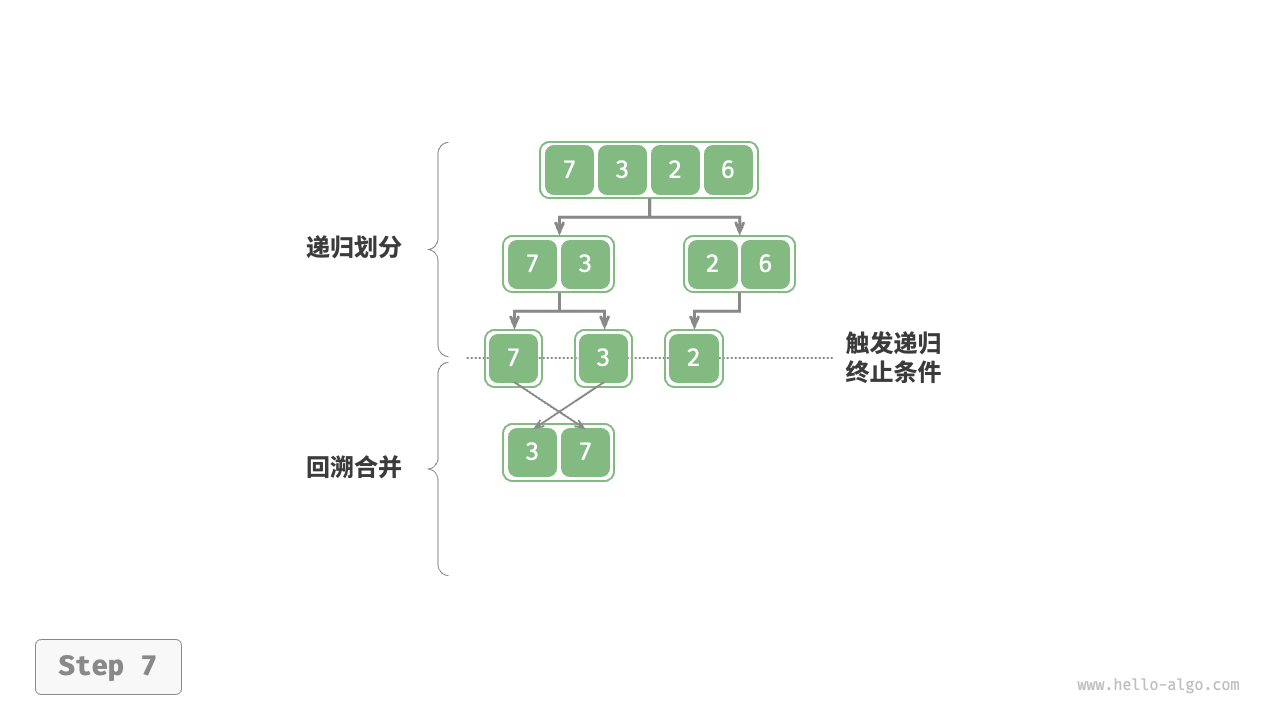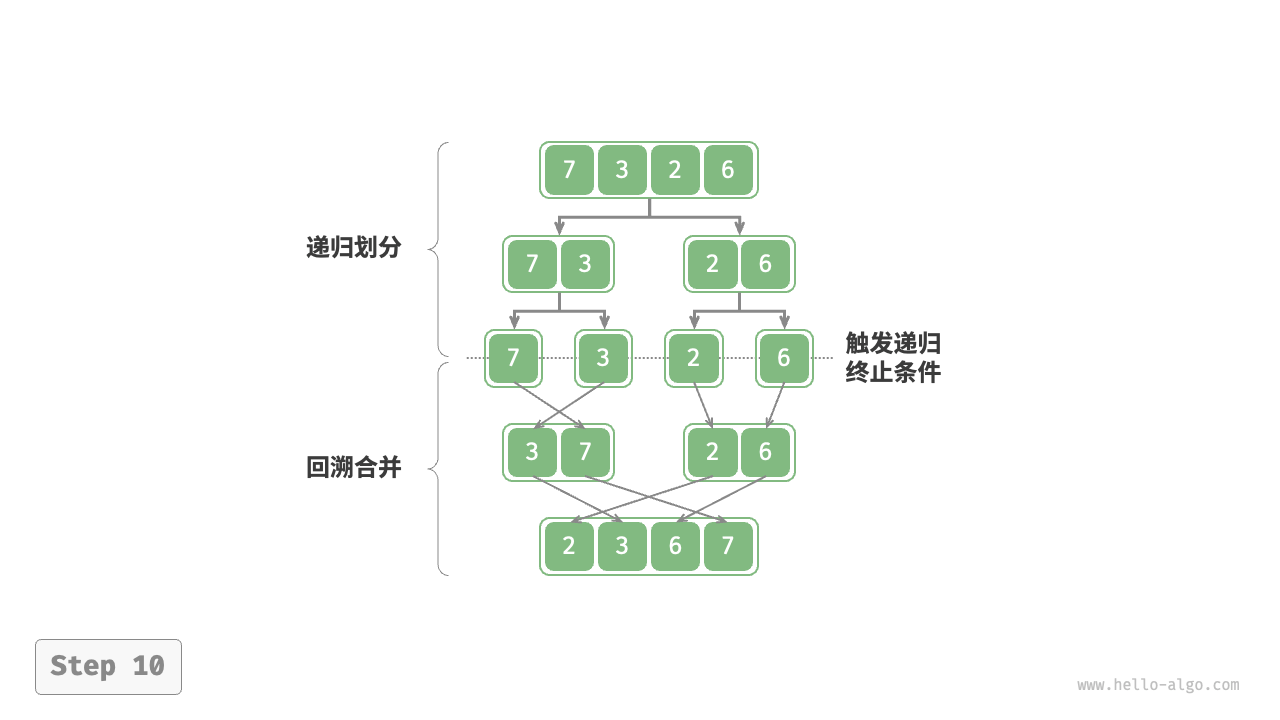
##代碼實現

1.向下遞歸，對半分割

2.遞歸返回條件：遞歸到最小，1個就是有序【控制的是范圍，歸并的是區間】

3.遞歸到最深處，最小時，就遞歸回去，開始分割按對半分割出的范圍，將已有子序列合并，在tmp里面進行合并

4.再將tmp里形成的有序序列，拷貝回原數組【因下一次遞歸回去上一層的歸并過程中，會將數據在tmp中進行歸并，會將tmp中的數據覆蓋，因此要及時，拷】

//python代碼示例
def Merge(a, start, mid, end) :tmp = [] #創建一個臨時列表，用來存儲合并的值#兩段起點的開始l = startr = mid + 1#當兩段都沒到達末尾，則繼續循環，將其添加到tmpwhile l <= mid and r <= end :if a[l] <= a[r] :tmp.append(a[l])l += 1else :tmp.append(a[r])r += 1#此時肯定只剩下，單一的一個值，即將剩余元素塞入到tmp中tmp.extend(a[l:mid+1])tmp.extend(a[r:end+1])#將合并完成的元素，賦值到a原數組中for i in range(start,end+1):a[i] = tmp[i - start]print(start,end,tmp)def MergeSort(a,start,end) :#利用遞歸來實現歸并排序，將大的問題分解成小的子問題if start == end : #當遞歸到數組只有一個元素時，直接返回returnmid = (start + end) // 2 #計算出mid，找到遞歸點MergeSort(a,start,mid) #左遞歸MergeSort(a,mid+1,end) #右遞歸Merge(a,start,mid,end)#左遞歸，左合并，右遞歸，右合并，類似于樹的后序遍歷a = [7,3,2,6]
MergeSort(a,0,3)

//c++代碼實現示例
#include<iostream>
#include<vector>
using namespace std;
//c++代碼實現示例
void merge(vector<int> &a, int left, int mid, int right)
{int i = left ;int j = mid + 1 ;int k = left ;vector<int> tmp(right - mid + 1) ;while ( i <= mid && j <= right ){if ( a[i] <= a[j] ){tmp[k++] = a[i++] ;}else{tmp[k++] = a[j++] ;}}while ( i <= mid ){tmp[k++] = a[i++] ;}while ( j <= right ){tmp[k++] = a[j++] ;}for (int m = left ; m <= right ; m++){a[m] = tmp[m - left] ;}cout << left << right << " " ;for (int n = 0 ; n < tmp.size() ; ++n){cout << tmp[n] << " " ;}
}void mergeSort(vector<int> &a, int left, int right)
{if (left >= right){return ;}int mid = (left + right) / 2 ;mergeSort(a,left,mid) ;mergeSort(a,mid+1,right) ;merge(a,left,mid,right) ;
}int main()
{
//	vector<int> arr = {1,2,3,4,5};
//	vector<int> arr;arr.push_back(7);arr.push_back(3);arr.push_back(2);arr.push_back(6);
//    arr.push_back(5);mergeSort(arr,0,3) ;return 0 ;}

void _MergerSort(DataType* a ,DataType* tmp, int begin,int end)
{//遞歸返回條件，不正常的范圍，或只剩下一個數 if (begin >= end){return ;}int mid = (begin + end) / 2 ;//遞歸過程 _MergeSort(a,tmp,begin,mid) ;_MergeSort(a,tmp,mid+1,end) ;//合并過程 //歸并到tmp數組中，再拷貝回去 int begin1 = begin ;int end1 = mid ;int begin2 = mid + 1 ;int end2 = end ;//指向tmp,=begin是 根據要進行比較插入的數組的位置 找到其對應在tmp中所對應的位置，則不會覆蓋前面已經排好序的數據int index = begin ;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin++] ;}else{tmp[index++] = a[begin2++] ;}}//剩下還沒有插入進去的 while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++] ;}//拷貝回去原數組a中memcpy(a+begin,tmp+begin,sizeof(DataType)*(end-begin+1)) ; 
}void MergeSort(DataType* a, int n)
{DataType* tmp = (DataType*)malloc(sizeof(DataType)*n) ;if (tmp == NULL){perror("malloc fail") ;return ;}_MergeSort(a,tmp,0,n-1) ;free(tmp) ;
}

對于鏈表，歸并排序相較于其他排序算法具有顯著優勢，可以將鏈表排序任務的空間復雜度優化至?𝑂(1)?。

劃分階段：可以使用“迭代”替代“遞歸”來實現鏈表劃分工作，從而省去遞歸使用的棧幀空間。
合并階段：在鏈表中，節點增刪操作僅需改變引用（指針）即可實現，因此合并階段（將兩個短有序鏈表合并為一個長有序鏈表）無須創建額外鏈表。

##非遞歸實現歸并排序

##釋

歸并排序時二分的思想=>logN層=>遞歸不會太深、且現在編譯器優化后，遞歸、非遞歸的性能差距沒有特別大了=>所以可以不用考慮非遞歸。

遞歸的缺點：遞歸消耗棧幀，遞歸的層數太深，容易爆棧。

【棧的空間比較小，在x86(32位)環境下，只有8M。（對比同一環境下的堆，則有2G+）。因為平時函數調用開不了多少個棧幀。理論上遞歸深度>1w 可能就會爆，但實際上5k左右就爆掉了】，這時就需要改非遞歸了。

非遞歸改寫方法：

1.改變循環

2.利用數據結構棧（本質是通過malloc在堆上開辟的存儲空間，內存空間需要足夠大）

3.遞歸逆著求-實際上也差不多也是遞歸思想（如斐波那契數列逆著來求也是可行的）

#代碼實現

開辟新的數組（臨時存放）用于歸并排序過程
int gap=1；gap*=2【gap控制歸并的范圍：11歸并，22歸并，44歸并】
for (int i = 0; i < n; i += 2 * gap) { 【i 控制進行比較輪到的組號，控制進行歸并的組號】
歸并完一輪，將歸并好的有序數組拷貝回原數組memcpy 。
進入新的一輪歸并，直至gap>n則歸并完成

?????☆注意的兩個情況

?????6. if (begin2 >= n) { break; } 第二組不存在，這一組不用歸并了?

? ? ?7. if (end2 > n) { end2 = n - 1; } 第二組右邊界越界問題，修正一下

void MergerSortNonR(DataType* a, int n)
{DataType* tmp = (DataType*)malloc(sizeof(DataType) * n); ? //開辟新的數組（臨時存放）用于歸并排序過程if (tmp == NULL){perror("malloc fail") ;return ;}int gap = 1 ;while (gap < n)?{for (int i = 0 ; i < n ; i += 2 * gap){
//?? ??? ??? ?// 1 , 1 歸并?
//?? ??? ??? ?// 2 , 2 歸并
//?? ??? ??? ?//4 , 4 歸并?
//?? ??? ??? ?//[begin1,end1][begin2,end2]歸并?int begin1 = i ;int end1 = i + gap - 1 ;int begin2 = i + gap ;int end2 = i + 2 * gap - 1 ;//?? ??? ??? ?//如果第二組不存在，這一組不用歸并了if (begin2 >= n)?{break;}//第二組右邊界越界問題，修正一下if (end2 > n)?{end2 = n - 1;}
//?? ??? ??? ?
//?? ??? ??? ?//當beigin2 超過 n 的時候，直接break掉就OK了
//?? ??? ??? ?//但end2 超過 n 的時候，需要修改邊界問題 n - 1?
//?? ??? ??? ?int index = i ;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++] ;}else{tmp[index++] = a[begin2++] ;}}while (begin1 <= end1){tmp[index++] = a[begin1++] ;}while (begin2 <= end2){tmp[index++] = a[begin2++];}
//?? ??? ??? ?//為什么這里不能是，2 * gap呢，不一定是2*gap的數都拷貝過去，memcpy(a+i,tmp+i,sizeof(DataType)*(end2 - beigin1 + 1)) 錯誤?
//?? ??? ??? ?// memcpy(a+i,tmp+i,sizeof(DataType)*(end2 - begin1 + 1)) ; 因為begin1++會發生改變的，因此不可以，錯誤?memcpy(a+i,tmp+i,sizeof(DataType)*(end2 - i + 1)) ;
//?? ??? ??? ?
//?? ??? ?}printf("\n");
//?? ??? ?for (int k = 0 ; tmp.size() ; k ++)
//?? ??? ?{
//?? ??? ??? ?printf("%d",tmp[k]) ;
//?? ??? ?}gap = gap * 2 ;}free(tmp);
}
}

def MergeSort(a, n) :tmp = [0] * (n+1)gap = 1while (gap < n) :z = gap * 2for i in range(0,n,z) :begin1 = iend1 = i + gap - 1begin2 = i + gapend2 = i + 2 * gap - 1if begin2 > n :breakif end2 > n :end2 = n - 1index = iwhile begin1 <= end1 and begin2 <= end2 :if a[begin1] < a[begin2] :tmp[index] = a[begin1]index += 1begin1 += 1else :tmp[index] = a[begin2]index += 1begin2 += 1while begin1 <= end1 :tmp[index] = a[begin1]index += 1begin1 += 1while begin2 <= end2 :tmp[index] = a[begin2]index += 1begin2 += 1for j in range(i,end2 + 1) :a[j] = tmp[j - i]print()# print(tmp)gap = gap * 2