【數據結構】二叉樹(Binary Tree)

文章目錄

一、樹的概念及結構
二、二叉樹的概念及結構
- 1.二叉樹的概念
- 2.特殊的二叉樹
- 3.二叉樹的性質
三、二叉樹的存儲
- 順序存儲
- 鏈式存儲
四、二叉樹的實現
- 1.創建二叉樹
- 2.二叉樹的遍歷
- - 前序遍歷
  - 中序遍歷
  - 后序遍歷
  - 層序遍歷
  - 根據遍歷順序創建二叉樹
- 3.二叉樹的基本操作
- - 1.總結點個數
  - 2.二叉樹高度
  - 3.第K層結點個數
  - 4.查找
  - 5.判斷二叉樹是否是完全二叉樹
- 4.銷毀二叉樹

一、樹的概念及結構

樹是一種非線性的數據結構，它是由n（n>=0）個有限結點組成一個具有層次關系的集合。它看起來像一棵倒掛的樹，根朝上，而葉子朝下，所以我們把它叫做為樹。
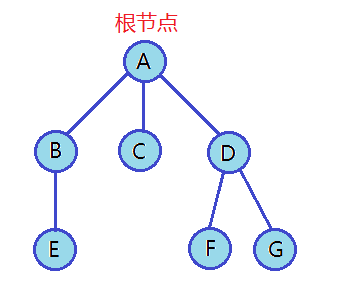
在這里插入圖片描述

根結點：沒有前驅結點，是當前樹中所有結點的祖先。

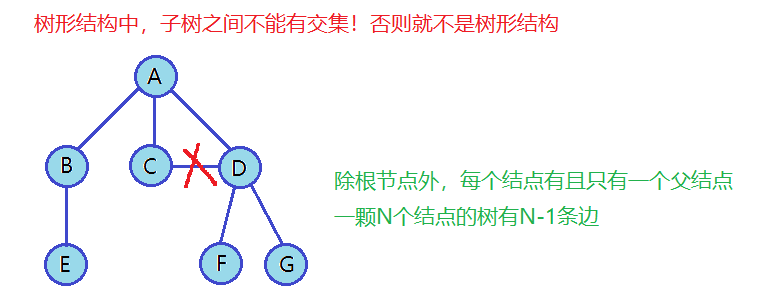
除根節點外，其余結點被分成一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅，可以有0個或多個后繼。因此，樹是遞歸定義的。

節點的度：一個節點含有的子樹的個數稱為該節點的度；如上圖：A的度為3。

葉子節點：度為0的節點稱為葉子節點；如上圖：E、F、G為葉子節點。

雙親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點；如上圖：A是B的父節點，B是E的父節點。

孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點；如上圖：B是A的子節點，F是D的子節點。

兄弟節點：具有相同父節點的節點互稱為兄弟節點；如上圖：B、C、D是兄弟節點。

樹的度：一棵樹中，最大的節點的度稱為樹的度；如上圖：樹的度為3.

節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推；

樹的高度或深度：樹中節點的最大層次/深度；如上圖：樹的高度為3

堂兄弟節點：雙親在同一層的節點互為堂兄弟；如上圖：E、F互為堂兄弟節點

節點的祖先：從根到該節點所經分支上的所有節點；如上圖：A是所有節點的祖先

子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫

森林：由m（m>0）棵互不相交的樹的集合稱為森林；

二、二叉樹的概念及結構

1.二叉樹的概念

二叉樹是一種特殊的樹，每個結點最多只能有兩個子結點，即二叉樹不存在度大于2的結點。
二叉樹可以分為三個部分：根、左子樹、右子樹，每顆子樹又可以劃分為這三個部分，一直遞歸到葉子結點，葉子結點是其本身的根結點。
二叉樹的子樹有左右之分，次序不能顛倒，因此二叉樹是有序樹。
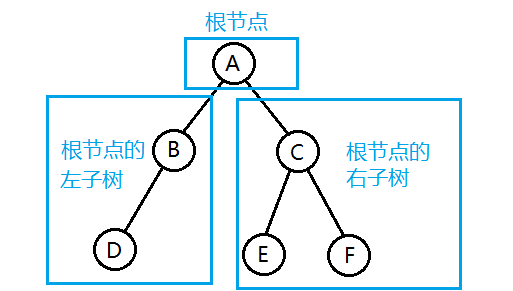
在這里插入圖片描述

二叉樹有五種基本形態：空樹(B的右子樹)、只有根節點(D、E、F)、只有左子樹(B)、只有右子樹、左右子樹(A、C)都存在。

2.特殊的二叉樹

滿二叉樹：除了葉子結點之外的所有結點都有兩個子結點。如果一個滿二叉樹的層數為K，那么結點總數是2⁰ + 2¹ + … + 2^k-1 = 2^k - 1個。

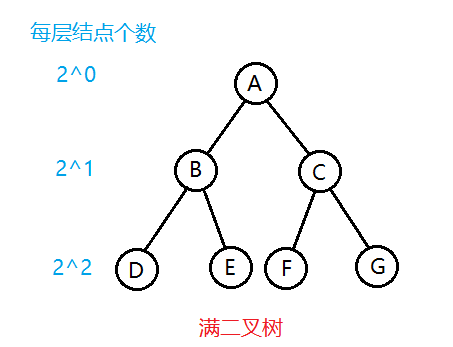
在這里插入圖片描述

完全二叉樹：除了最后一層，完全二叉樹的每一層從左到右都是滿的。也就是說，如果完全二叉樹的層數為 h，那么前 h-1 層一定是一個滿二叉樹。
滿二叉樹是一種特殊的完全二叉樹。

在這里插入圖片描述

斜二叉樹：除了葉子結點外，所有結點都只有一個結點，且是一個方向的結點，要么都只有左結點，要么都只有右結點。

在這里插入圖片描述

3.二叉樹的性質

1.任意二叉樹第 i 層最多有2^i-1個結點。 ( i $\geq$ 1)
2.深度為 h 的任意二叉樹的最大結點總數為2^h-1。( h $\geq$ 1)
3.任意二叉樹中，度為0的葉子結點個數永遠比度為2的結點個數多一個。
4.對于一個有n個結點的滿二叉樹，其深度 h= $log_2$ (n+1)（向上取整）

三、二叉樹的存儲

二叉樹一般可以使用兩種結構存儲，一種順序結構，一種鏈式結構。

順序存儲

二叉樹的順序結構存儲就是使用數組來存儲。按照層序遍歷的順序（從上到下，從左到右）依次將結點存儲在數組中，如果某個結點的左結點或者右結點不存在，則對應的數組的位置就為空，不存儲元素。
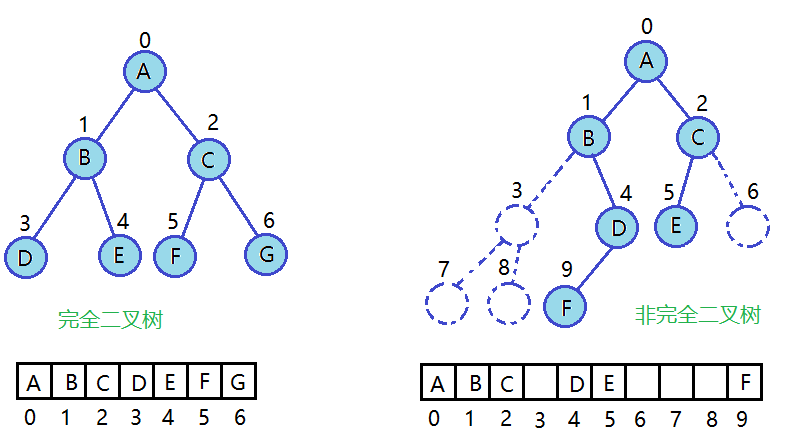
在這里插入圖片描述

二叉樹順序存儲在物理上是一個數組，在邏輯上是一顆二叉樹。
二叉樹以數組方式存儲，父子結點下標的關系：左結點下標 = 2*父結點下標+1，右結點下標 = 2*父結點下標+2，父結點下標 = （任意孩子結點下標-1）/ 2。
由上圖可以看出，如果是非完全二叉樹用數組來表示，則會存在空間浪費，所以使用數組一般只適合表示完全二叉樹。而對于一般的二叉樹，常用鏈式存儲結構。

鏈式存儲

二叉樹的鏈式存儲結構是指，用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關系。通常的方法是鏈表中每個結點由三個域組成，數據域和左右指針域，左右指針分別用來存儲該結點左孩子和右孩子所在結點的存儲地址。

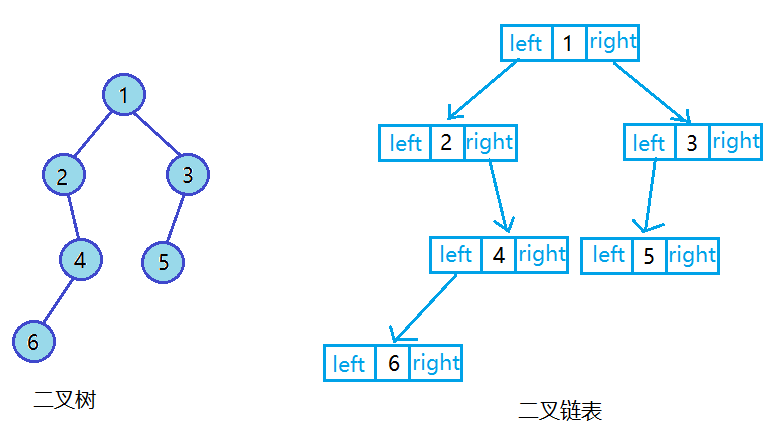
在這里插入圖片描述

四、二叉樹的實現

接下來我們用鏈表來實現二叉樹的創建與遍歷。

二叉樹定義

typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;//數據struct BinaryTreeNode* left;//左孩子結點struct BinaryTreeNode* right;//右孩子結點
}BTNode;

1.創建二叉樹

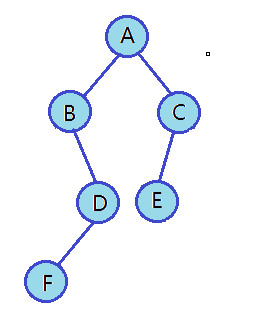
在這里插入圖片描述

以上圖為例建立一棵二叉樹。
以下代碼并不是真正創建二叉樹的方式，只是為了方便大家理解，所以手動快速創建一棵簡單的二叉樹。等后面學完二叉樹遍歷之后，我們再講解二叉樹的真正創建方式。

//動態申請結點
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (NULL == node){perror("malloc");return NULL;}node->data = x;node->left = node->right = NULL;return node;
}
//創建二叉樹
BTNode* CreatTree()
{BTNode* node1 = BuyNode('A');BTNode* node2 = BuyNode('B');BTNode* node3 = BuyNode('C');BTNode* node4 = BuyNode('D');BTNode* node5 = BuyNode('E');BTNode* node6 = BuyNode('F');node1->left = node2;node1->right = node3;node2->right = node4;node3->left = node5;node4->left = node6;return node1;
}

2.二叉樹的遍歷

前面我們講過，二叉樹分為：根、左子樹、右子樹。每個結點的左右子樹又可以劃分為這三個部分，直到最后一層的葉子結點，葉子結點是其本身的根結點，左右結點為空。根據這一特點，可以看出，二叉樹定義是遞歸式的。
二叉樹遍歷是按照某種特定的規則，依次訪問每個節點，并且每個節點只訪問一次。根據根節點的訪問順序分為三種遍歷方式：前序遍歷、中序遍歷和后序遍歷。

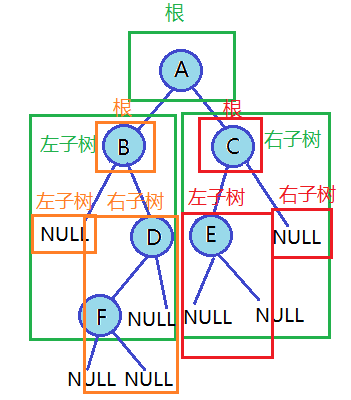
在這里插入圖片描述

前序遍歷

前序遍歷的訪問順序：根結點、左子樹、右子樹。
其中，對于每棵子樹，訪問順序也是根結點、左子樹、右子樹，一直遞歸到空結點。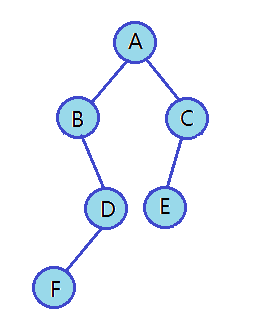

在這里插入圖片描述

在這里插入圖片描述相同顏色框的是相同根節點的左右子樹

比如上圖的前序遍歷訪問順序為：A B NULL D F NULL NULL NULL C E NULL NULL NULL
而我們一般不打印空結點，所以前序遍歷結果為：A B D F C E

//前序遍歷
void PreOrder(BTNode* root)
{if (NULL == root){//printf("NULL ");return;}printf("%c ", root->data);//打印根節點的值PreOrder(root->left);//遍歷子樹PreOrder(root->right);//遍歷右子樹
}

中序遍歷

中序遍歷的訪問順序：左子樹、根結點、右子樹。
還是拿上圖示例，中序遍歷訪問順序為：NULL B NULL F NULL D NULL A NULL E NULL C NULL
去掉空結點后，中序遍歷結果為：B F D A E C
在這里插入圖片描述

在這里插入圖片描述

//中序遍歷
void InOrder(BTNode* root)
{if (NULL == root){//printf("NULL ");return;}InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}

后序遍歷

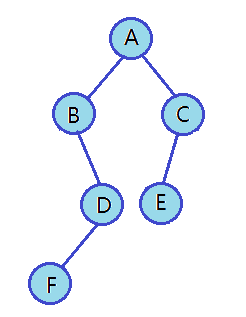
中序遍歷的訪問順序：左子樹、右子樹、根結點。

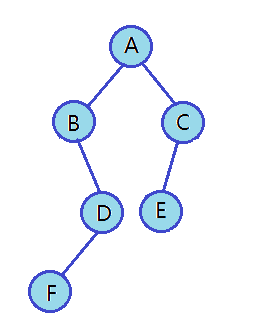
在這里插入圖片描述

在這里插入圖片描述上圖二叉樹的后序遍歷訪問順序為：NULL NULL NULL F NULL D B NULL NULL E NULL C A
去掉空結點后，后序遍歷結果為：F D B E C A

//后序遍歷
void PostOrder(BTNode* root)
{if (NULL == root){//printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}

層序遍歷

二叉樹的層次遍歷最好理解，從二叉樹的根結點開始，從上到下每一層按照從左到右的順序遍歷。比如上圖中二叉樹的層序遍歷為：A B C D E F

前面三種遍歷都是以遞歸的形式，而層序遍歷可以用隊列來實現非遞歸遍歷。前面我們已經用C語言寫過隊列（點擊跳轉文章）結構，可以在vs中直接將隊列的相關代碼copy過來使用，在源文件和頭文件中直接添加現有項即可。

并將隊列中的類型改為二叉樹類型

//typedef int QDataType;
typedef struct BinaryTreeNode* QDataType;

具體過程是：先將當前節點入隊列，訪問當前結點，再將當前結點出隊列。然后將當前結點的左結點和右結點按順序入隊，如果為空結點則不用入隊，直到隊列為空。

//層序遍歷
void LevelOrder(BTNode* root)
{assert(root);Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);if(front->left != NULL)QueuePush(&q, front->left);if (front->right != NULL)QueuePush(&q, front->right);}QueueDestroy(&q);printf("\n");
}

根據遍歷順序創建二叉樹

數組a存儲前序遍歷的順序，比如通過前面我們知道二叉樹的前序遍歷結果為A B NULL D F NULL NULL NULL C E NULL NULL NULL ；我們將NULL替換成字符#表示空。數組下標用指針接收，否則遞歸函數中不會改變實參。

//根據前序遍歷的順序二叉樹創建
BTNode* BTreeCreate_PreOrder(BTDataType* a, int* pi)
{// 通過前序遍歷的數組"AB#DF###CE###"構建二叉樹if (a[*pi] == '#'){(*pi)++;//數組下標+1return NULL;}BTNode* node = BuyNode(a[*pi]);//根據數組元素構建二叉樹結點(*pi)++;node->left = BTreeCreate_PreOrder(a, pi);node->right = BTreeCreate_PreOrder(a, pi);return node;
}

根據中序/后序順序來構建二叉樹同理。

int main()
{char a[] = "AB#DF###CE###";int i = 0;BTNode* root = BTreeCreate_PreOrder(a, &i);//BTNode* root = BTreeCreate();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);printf("\n");return 0;
}

3.二叉樹的基本操作

在前面二叉樹遞歸遍歷的基礎上，我們可以實現一些二叉樹的基本操作。

1.總結點個數

轉換成子問題：二叉樹總結點個數=1（根節點個數）+ 左子樹的結點個數 + 右子樹的節點個數。很容易想到遞歸。

//二叉樹的總結點個數
int BTreeSize(BTNode* root)
{if (NULL == root){return 0;}return 1 + BTreeSize(root->left) + BTreeSize(root->right);
}

2.二叉樹高度

當前樹的高度 = 左右子樹中比較高的高度+1

//二叉樹的高度
int BTreeLevel(BTNode* root)
{if (NULL == root)//空結點則返回0{return 0;}int leftLevel = BTreeLevel(root->left);//左子樹的高度int rightLevel = BTreeLevel(root->right);//右子樹的高度return leftLevel > rightLevel ? leftLevel + 1 : rightLevel + 1;
}

最好不要寫成下面這樣，會造成重復遞歸，判斷時遍歷左右子樹遞歸兩次，返回結果時又遞歸一次，棧幀開銷會很大。

return BTreeLevel(root->left) > BTreeLevel(root->right) ? BTreeLevel(root->left) + 1 : BTreeLevel(root->right) + 1;

3.第K層結點個數

求第K層結點個數，轉換成子問題：求左子樹第K-1層結點個數 + 右子樹第K-1層結點個數

//第k層結點的個數
int BTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);//默認根節點為第一層，所以不存在第0層if (NULL == root)//空結點{return 0;}if (1 == k)//遍歷到第k層{return 1;}return BTreeLevelKSize(root->left, k-1)+BTreeLevelKSize(root->right, k-1);
}

4.查找

//查找值為x的結點
BTNode* BTreeFind(BTNode* root, BTDataType x)
{if (NULL == root)return NULL;if (root->data == x)return root;BTNode* left = BTreeFind(root->left, x);if (left)//左子樹找到則返回return left;//左子樹未找到，只可能存在于右子樹return BTreeFind(root->right, x);
}

5.判斷二叉樹是否是完全二叉樹

完全二叉樹按層序走，非空結點一定是連續的。每次將當前結點的左右結點入隊列，不用判空，空結點也入隊列。遇到第一個空結點時，停止入隊，開始判斷隊列中的元素是否都為空，若出現非空結點，說明不是完全二叉樹，反之則是完全二叉樹。

//判斷二叉樹是否是完全二叉樹
bool BTreeComplete(BTNode* root)
{assert(root);Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//完全二叉樹按層序走，非空結點一定是連續的if (NULL == front)//遍歷到第一個空結點則退出循環，進入下個while循環判斷{break;}else{//不為空則將左右孩子結點入隊QueuePush(&q, front->left);QueuePush(&q, front->right);}}//如果是完全二叉樹，則隊列中元素全是NULLwhile (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//有非空結點則說明非空結點不是完全連續，說明不是完全二叉樹if (front != NULL){QueueDestroy(&q);//返回之前及時釋放空間,防止內存泄露return false;}}QueueDestroy(&q);return true;
}

4.銷毀二叉樹

根節點最后釋放，否則無法訪問左右子樹。

//二叉樹銷毀（后序遍歷）
void BTreeDestroy(BTNode* root)
{if (NULL == root)return;BTreeDestroy(root->left);BTreeDestroy(root->right);free(root);root = NULL;
}

完整代碼：鏈式二叉樹