參考文章:
一文弄懂神經網絡中的反向傳播法——BackPropagation - Charlotte77 - 博客園
反向傳播求偏導原理簡單理解_反向傳播偏導-CSDN博客
這篇文章是筆者在讀完上述兩篇參考文章后的整理或者說按照自己的理解進行的一些補充,強烈推薦先閱讀上述兩篇文章。這兩篇文章一篇籠統的介紹了神經網絡反向傳播的通過鏈式法則計算的原理,一篇采用具體的實例進行講解,非常易于理解。
如何優化神經網絡中的權重?
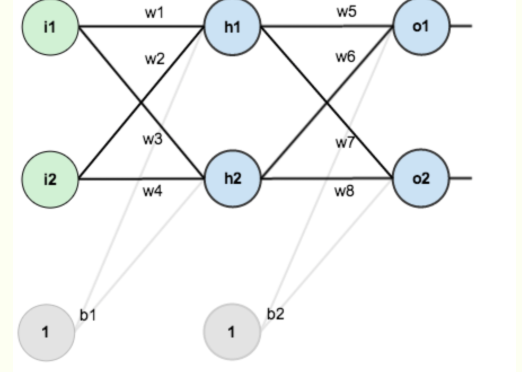
比如針對上面的這個神經網絡,其中有w1,w2..b1,b2等權重參數,這些參數都是待優化的對象。一般進行優化的方式就是:計算最終的損失函數對某個權重的偏導。
比如想優化w1這個權重,那么就需要計算:這個式子的含義就是:權重w1對于最終的損失L有多少的貢獻。
為什么這個式子能夠表達這樣的含義?需要回到偏導數的定義來看:
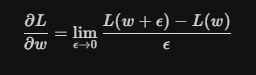
這個式子的含義就是,權重w增加一個極小的量,損失函數L變化了多少?這個變化量,其實就衡量了權重w對L的貢獻。更形象的理解,假設w是一個旋鈕,我極其輕微的轉動了(轉動量就是
)一下這個旋鈕,發現最終結果變化非常大,是不是就意味著w的貢獻非常大。
得到了偏導的計算結果,之后就可以通過引入一個權重因子來對參數w1進行優化:
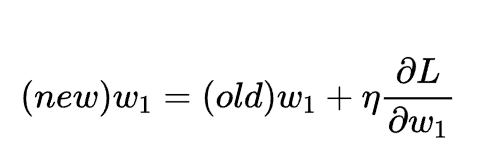
如何計算損失函數對某個權重的偏導?
針對上面的那張神經網絡的情況,本質上可以用如下的計算流程進行表示。這里具體的操作如何計算損失函數對某個權重的偏導,記錄在以下稿紙上。不過需要說明的幾點是:
1、強烈推薦看之前的兩篇參考文章,這里的計算是基于前面文章中涉及的問題的,很多地方都是自字母表示;
2、計算方向傳播的過程本質上是利用鏈式法則,理解之后其實非常簡單;
3、為了能夠利用鏈式法則,在每一步的前向傳播過程中,其實會計算臨時變量比如這里的h1,o1等對各個權重的偏導,因為最終損失函數對權重的偏導需要用到這些數據;

關于梯度下降法的理解:
我們計算損失函數對某個權重的偏導,這其實只是一個維度,真正決定損失函數朝著哪個方向優化的,其實是損失函數對所有權重的偏導所構成的向量,如下公式所示:
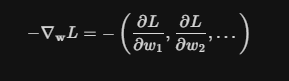
)








頂級父類與它的重要方法equals())
實現時間序列預測:從數據到閉環預測全解析)


)




(按鍵設置及中斷設置)
