字符串

字符串算法題目主要處理文本的查找、匹配、比較、變換和統計問題，其核心特點是輸入數據為字符序列，解題關鍵在于利用其連續性、前綴性、字典序等特性，并常借助哈希、自動機、指針滑動、動態規劃等技巧高效處理。

---

詳細分類型與適用場景

當一道題的輸入是一個或多個字符串時，你就應該考慮使用字符串算法。以下是主要的題目類型和適用場景：

1. 基礎操作與模擬

• 特點：直接考察對字符串的索引、遍歷、拼接、反轉等基本操作。

• 常見題型：字符串反轉、判斷回文串、實現基本的字符串轉換（如?atoi）、Z字形變換等。

• 適用場景：問題描述本身就像是在指導你一步步操作字符串。

2. 匹配與查找問題

這是字符串問題的核心領域。

• 特點：在一個主串（文本）中查找一個或多個模式串是否存在及出現的位置。

• 常見算法：

  • 暴力匹配：簡單但低效，適用于小規模數據。

  • KMP算法：高效的單模式串匹配，利用“部分匹配表”避免回溯。

  • Rabin-Karp算法：利用滾動哈希進行多模式串匹配的預處理。

  • 字典樹（Trie）：快速檢索字符串集合中是否存在某個前綴或整個字符串。

  • AC自動機：字典樹 + KMP?的思想，用于多模式串匹配的終極武器（如敏感詞過濾）。

• 適用場景：問題中出現“查找子串”、“所有出現位置”、“是否包含某些單詞”等關鍵詞。

3. 子串與子序列問題

• 特點：不要求連續（子序列）或要求連續（子串）的序列問題，常求最大、最小、最長、最短等。

• 常見題型：

  • 最長回文子串：使用中心擴散法或Manacher算法。

  • 最長公共子串/子序列（LCS）：經典動態規劃問題。

  • 最長不含重復字符的子串：使用滑動窗口（雙指針）的代表性問題。

  • 最短編輯距離：另一個經典的動態規劃問題，衡量兩個字符串的相似度。

• 適用場景：問題要求找到一個滿足特定條件的“序列”，且這個序列源自原字符串。

4. 計數與統計問題

• 特點：統計字符串中字符、子串、模式出現的頻率、數量或分布。

• 常見題型：統計字母出現次數、統計“優美子串”的數目、不同子串的個數等。

• 適用場景：問題中出現“有多少種”、“出現次數”、“頻率最高”等統計性詞匯。常結合哈希表來記錄頻率。

5. 分割與組合問題

• 特點：將字符串按一定規則進行分割，或者由多個部分組合成一個新字符串。

• 常見題型：單詞拆分、回文分割、恢復IP地址等。

• 適用場景：問題要求將字符串切割成若干段，每段需要滿足特定條件。這類問題通常使用回溯法（DFS）?或動態規劃來解決。

6. 表達式 parsing 與計算

• 特點：處理具有特定語法結構的字符串，如數學表達式、JSON、XML等。

• 常見題型：基本計算器（實現加減乘除括號）、逆波蘭表達式求值、解析HTML標簽等。

• 適用場景：輸入字符串具有明確的遞歸或嵌套結構。解決方案通常是使用棧或遞歸下降等解析方法。

7. 字符串排序與字典序問題

• 特點：利用字符串的字典序特性進行排序或比較。

• 常見題型：拼接所有字符串使字典序最小、最長快樂前綴、后綴數組等。

• 適用場景：問題要求比較字符串的“大小”或按特定順序排列字符串。

總結

當你看到問題的輸入是字符串，并且問題目標涉及查找、匹配、比較、變換、計數、分割這幾種操作時，它就是一個字符串算法題。解決它們的關鍵是選擇合適的數據結構（哈希表、Trie、棧）和算法思想（滑動窗口、動態規劃、回溯、自動機）。

題目練習

14. 最長公共前綴 - 力扣（LeetCode）

解法：

算法思路：

解法一（兩兩比較）：

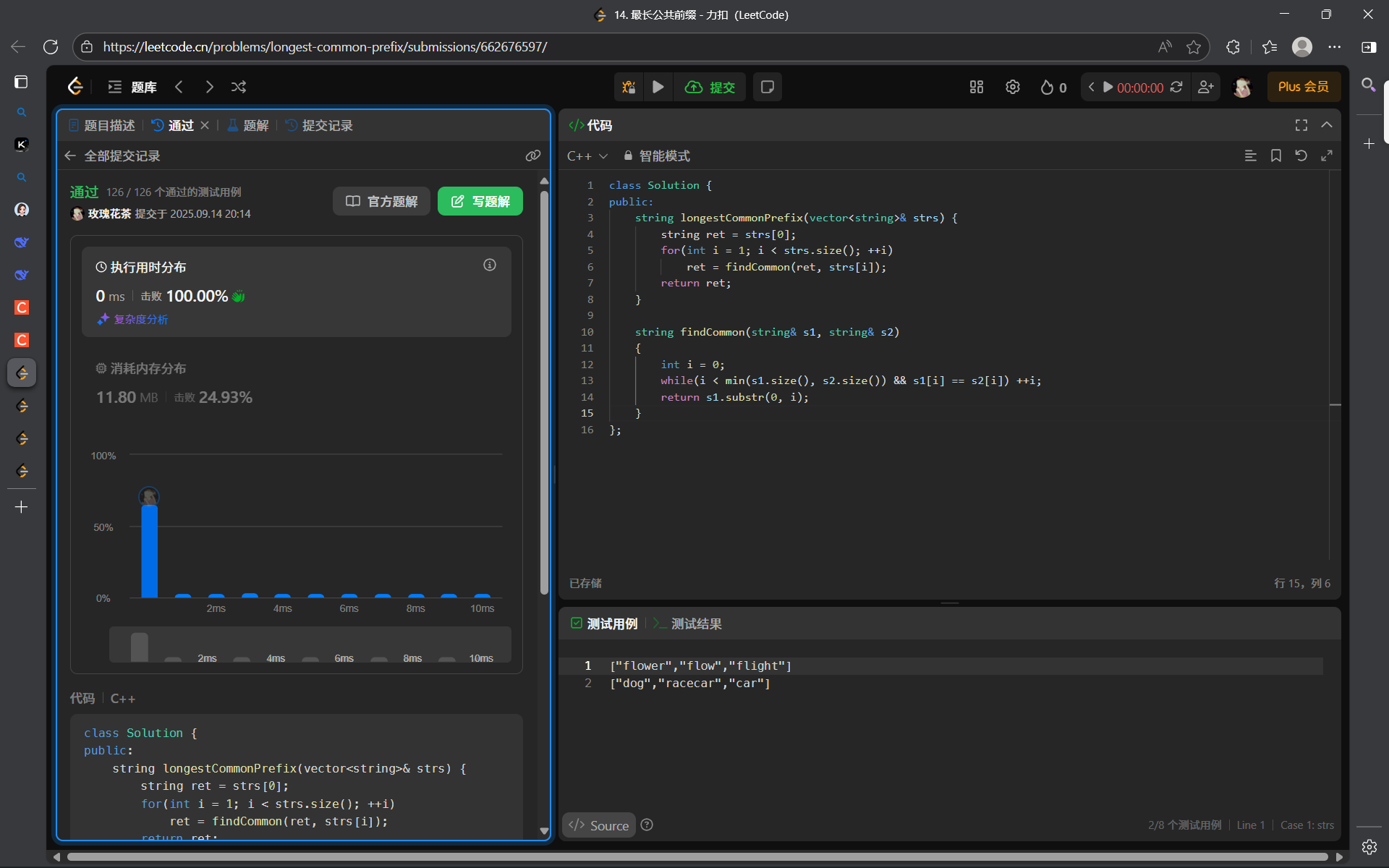
我們可以先找出前兩個的最長公共前綴，然后拿這個最長公共前綴依次與后面的字符串比較，這樣就可以找出所有字符串的最長公共前綴。

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {string ret = strs[0];for(int i = 1; i < strs.size(); ++i)ret = findCommon(ret, strs[i]);return ret;}string findCommon(string& s1, string& s2){int i = 0;while(i < min(s1.size(), s2.size()) && s1[i] == s2[i]) ++i;return s1.substr(0, i);}
};

解法二（統一比較）：

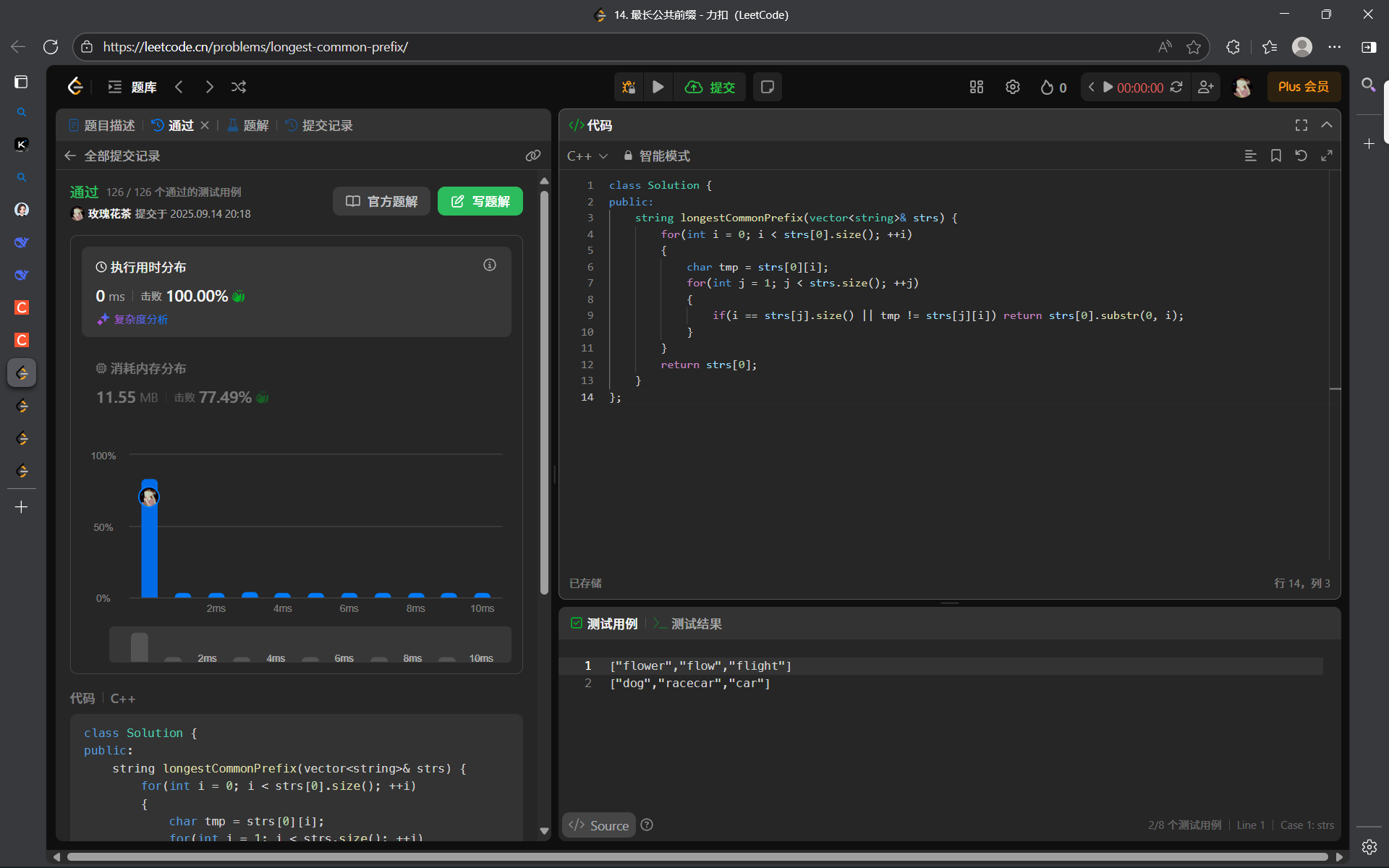
題目要求多個字符串的公共前綴，我們可以逐位比較這些字符串，哪一位出現了不同，就在哪一位截止。

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {for(int i = 0; i < strs[0].size(); ++i){char tmp = strs[0][i];for(int j = 1; j < strs.size(); ++j){if(i == strs[j].size() || tmp != strs[j][i]) return strs[0].substr(0, i);}}return strs[0];}
};

5. 最長回文子串 - 力扣（LeetCode）

解法（中心擴散）：

算法思路：

枚舉每一個可能的子串非常費時，有沒有比較簡單一點的方法呢？

對于一個子串而言，如果它是回文串，并且長度大于 2，那么將它首尾的兩個字母去除之后，它仍然是個回文串。如此這樣去除，一直除到長度小于等于 2 時呢？長度為 1 的，自身與自身就構成回文；而長度為 2 的，就要判斷這兩個字符是否相等了。

從這個性質可以反推出來，從回文串的中心開始，往左讀和往右讀也是一樣的。那么，是否可以枚舉回文串的中心呢？

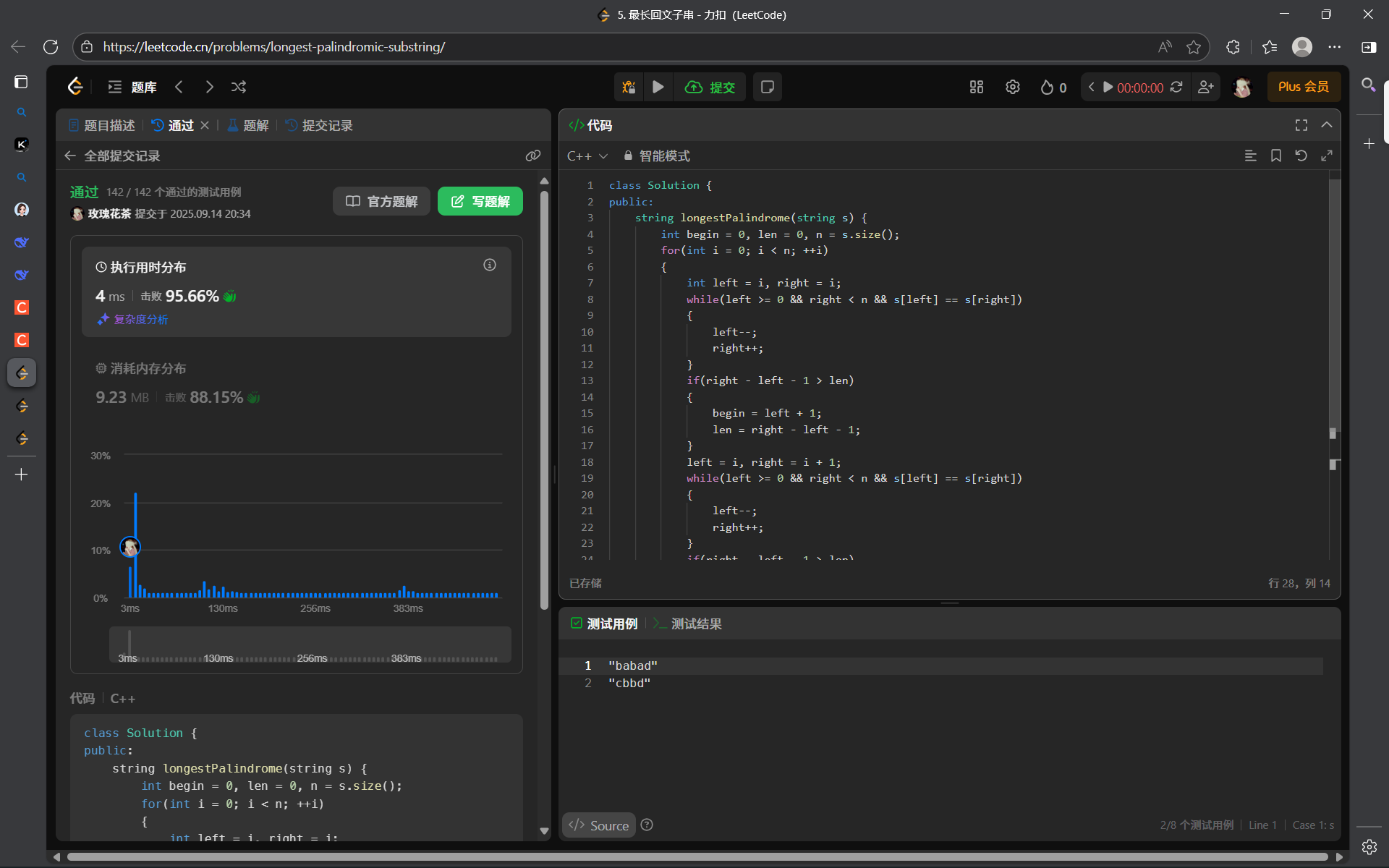
從中心向兩邊擴展，如果兩邊的字母相同，我們就可以繼續擴展；如果不同，我們就停止擴展。這樣只需要一層 for 循環，我們就可以完成先前兩層 for 循環的工作量。

class Solution {
public:string longestPalindrome(string s) {int begin = 0, len = 0, n = s.size();for(int i = 0; i < n; ++i){int left = i, right = i;while(left >= 0 && right < n && s[left] == s[right]){left--;right++;}if(right - left - 1 > len){begin = left + 1;len = right - left - 1;}left = i, right = i + 1;while(left >= 0 && right < n && s[left] == s[right]){left--;right++;}if(right - left - 1 > len){begin = left + 1;len = right - left - 1;}}return s.substr(begin, len);}
};

67. 二進制求和 - 力扣（LeetCode）

解法（模擬十進制的大數相加的過程）：

算法思路：

模擬十進制中我們列豎式計算兩個數之和的過程。但是這里是二進制的求和，我們不是逢十進一，而是逢二進一。

class Solution {
public:string addBinary(string a, string b) {string ret;int cur1 = a.size() - 1, cur2 = b.size() - 1, t = 0;while(cur1 >= 0 || cur2 >= 0 || t){if(cur1 >= 0) t += a[cur1--] - '0';if(cur2 >= 0) t += b[cur2--] - '0';ret += t % 2 + '0';t /= 2;}reverse(ret.begin(), ret.end());return ret;}
};

43. 字符串相乘 - 力扣（LeetCode）

解法（無進位相乘然后相加，最后處理進位）：

算法思路：

整體思路就是模擬我們小學列豎式計算兩個數相乘的過程。但是為了我們書寫代碼的方便性，我們選擇一種優化版本的，就是在計算兩數相乘的時候，先不考慮進位，等到所有結果計算完畢之后，再去考慮進位。如下圖：

class Solution {
public:string multiply(string num1, string num2) {int m = num1.size(), n = num2.size();reverse(num1.begin(), num1.end());reverse(num2.begin(), num2.end());vector<int> tmp(m + n - 1);for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){tmp[i + j] += (num1[i] - '0') * (num2[j] - '0');}}int cur = 0, t = 0;string ret;while(cur < m + n - 1 || t){if(cur < m + n - 1) t += tmp[cur++];ret += t % 10 + '0';t /= 10;}while(ret.size() > 1 && ret.back() == '0') ret.pop_back();reverse(ret.begin(), ret.end());return ret;}
};