????????本次我們分享點云法向量定向的四種方法,分別是XYZ軸、相機位置、最小生成樹(MST)和質心設定方法。通常出現在三維點云處理、三維重建、計算機視覺或圖形學中,需要估計點云的法向量方向。它們的核心任務是:在已知點坐標和局部幾何結構(如鄰域、最小生成樹)后,確定法向量的朝向(即指向“外側”還是“內側”)。
????????下面我分別介紹這四種方法的流程、優缺點和適用場景,并指出它們是如何解決法向量方向一致性這個關鍵問題的。
? 方法一:XYZ軸定向法(坐標軸對齊法)
🔧 流程:
1. 計算每個點的法向量(如PCA)。
2. 設定一個全局參考方向(通常是Z軸正方向,即 `(0,0,1)`)。
3. 將每個法向量與參考方向做點積:
- 若點積 < 0,則翻轉法向量方向。
4. 所有法向量朝向大致一致(如“朝上”)。? 優點:
- 簡單快速,無需額外結構。
- 適合大致水平分布的點云(如地面掃描、建筑物屋頂)。? 缺點:
- 對非水平、傾斜或復雜曲面無效。
- 無法處理封閉物體或多方向表面(如球體、人體)。????????📍應用場景:
- 地面點云(如LiDAR掃描的地面點)。
- 建筑物立面或屋頂提取。
- 快速預處理步驟。? 方法二:相機位置定向法(視角定向法)
🔧 流程:
1. 計算每個點的法向量(如PCA)。
2. 獲取相機或掃描儀的位置(已知或估算)。
3. 對于每個點,計算從該點到相機的向量(視線方向)。
4. 將法向量與視線方向做點積:
- 若點積 < 0,則翻轉法向量(使其“朝向”相機)。
5. 所有法向量朝向觀察者(即“外側”)。? 優點:
- 直觀有效,適合單視角掃描數據。
- 能處理復雜幾何形狀(如雕像、物體表面)。? 缺點:
- 需要已知相機位置或掃描儀軌跡。
- 對多視角拼接數據或封閉物體內部可能失效。
- 若物體有凹陷部分,可能出現方向錯誤。📍應用場景:
- 單視角RGB-D掃描(如Kinect、RealSense)。
- 三維重建中的點云預處理。
- 物體識別與渲染前的法向量統一。? 方法三:最小生成樹法(MST-based Orientation)
🔧 流程:
1. 構建點云的k近鄰圖或Delaunay三角網。
2. 以某點為根(如Z值最大點),構建最小生成樹(MST)。
3. 從根節點開始,沿MST傳播方向:
- 若相鄰點的法向量方向不一致(點積 < 0),則翻轉。
4. 最終所有法向量在連通區域內保持一致。? 優點:
- 無需相機信息,適合封閉物體。
- 能處理復雜拓撲結構(如人體、雕塑)。
- 全局一致性較好。? 缺點:
- 依賴連通性,對噪聲或離散點敏感。
- 若物體有非流形結構或多個連通分量,可能失敗。
- 計算復雜度較高(O(n log n))。📍應用場景:
- 封閉物體掃描(如文物、人體、雕像)。
- 無相機信息的點云(如激光掃描拼接后)。
- 三維重建前的法向量預處理。? 方法四:質心定向法(Centroid-based Orientation)
🔧 流程:
1. 計算每個點的法向量(如PCA)。
2. 計算整個點云的質心(幾何中心)。
3. 對于每個點,計算從質心到該點的向量(外指方向)。
4. 將法向量與該向量做點積:
- 若點積 < 0,則翻轉法向量(使其“朝外”)。
5. 所有法向量大致朝向“外側”。? 優點:
- 簡單快速,無需額外結構。
- 適合凸形物體(如球體、盒子、水果)。? 缺點:
- 對非凸物體(如杯子、椅子、人體)可能失效。
- 若質心在物體外部(如環形、U形),方向會混亂。
- 無法處理多連通分量或空心結構。📍應用場景:
- 凸形物體識別(如工業零件、水果檢測)。
- 快速初始化方向(后續再用MST refine)。
- 教學演示或簡單幾何體處理。? 總結對比表:
方法 是否需相機 是否需拓撲 是否全局一致 適合場景 主要缺點 XYZ軸法 ? ? ? 地面、屋頂 無法處理傾斜或封閉物體 相機法 ? ? ? 單視角掃描 需相機位姿,多視角失效 MST法 ? ? ? 封閉物體、無相機 噪聲敏感,計算量大 質心法 ? ? ? 凸形物體 非凸物體失效 ? 實際建議(組合使用):
- 先PCA求法向量 → 再用MST或相機法定向。
- 若有相機:優先用相機法。
- 若無相機且物體封閉:用MST法。
- 若是地面點云:直接用Z軸法。
- 若是凸形物體:可用質心法快速初始化。
本次我們使用的數據是————兔砸!
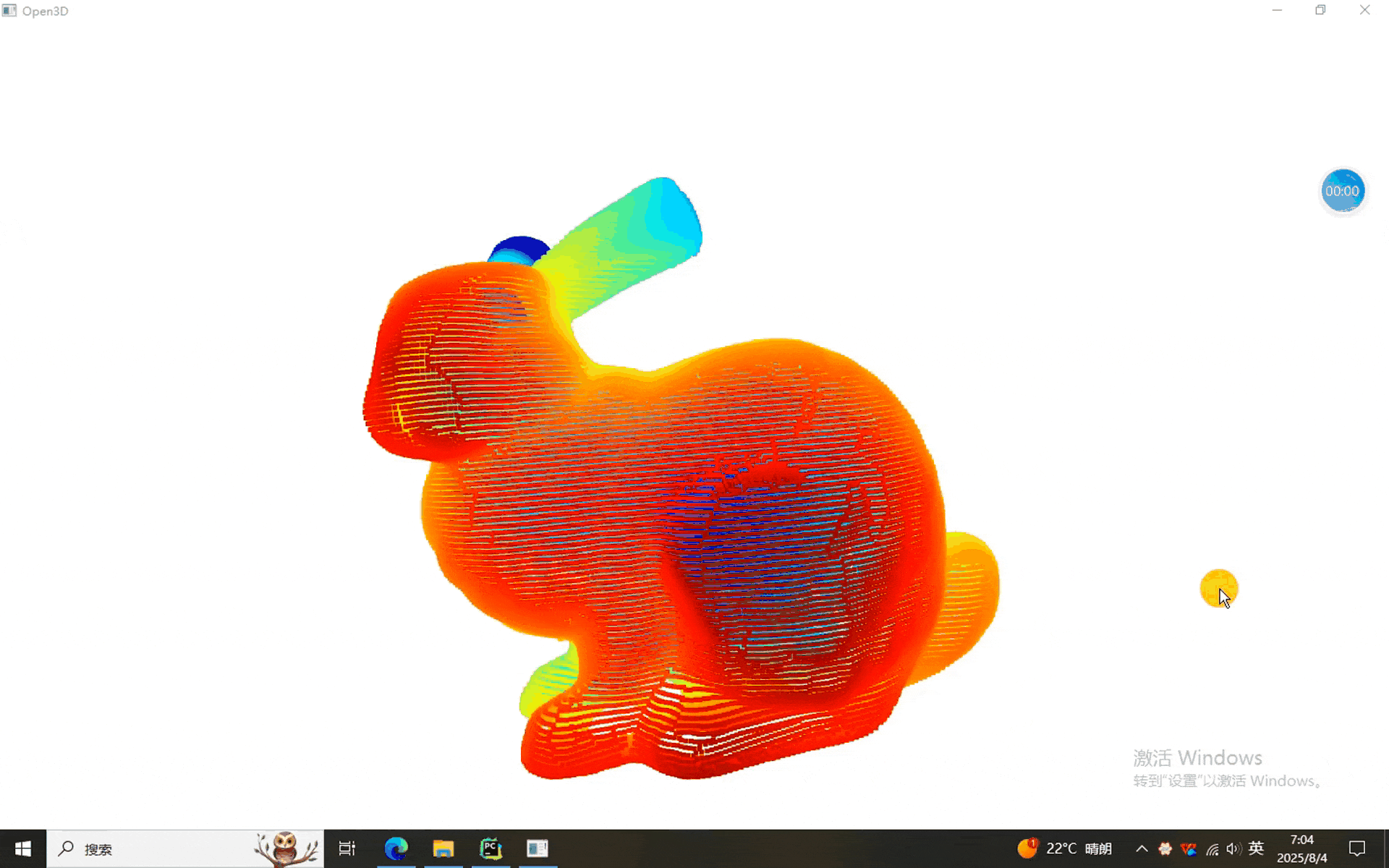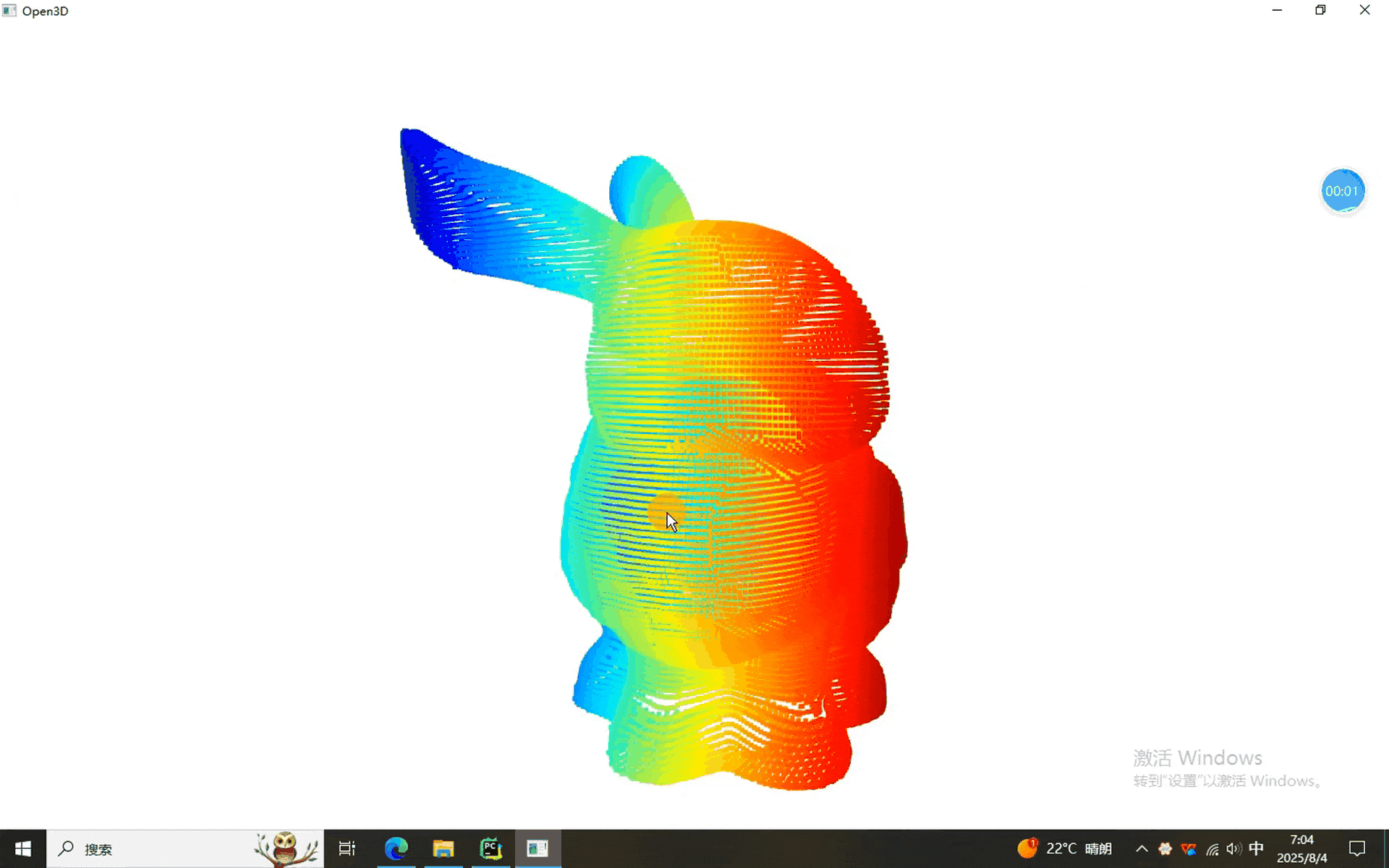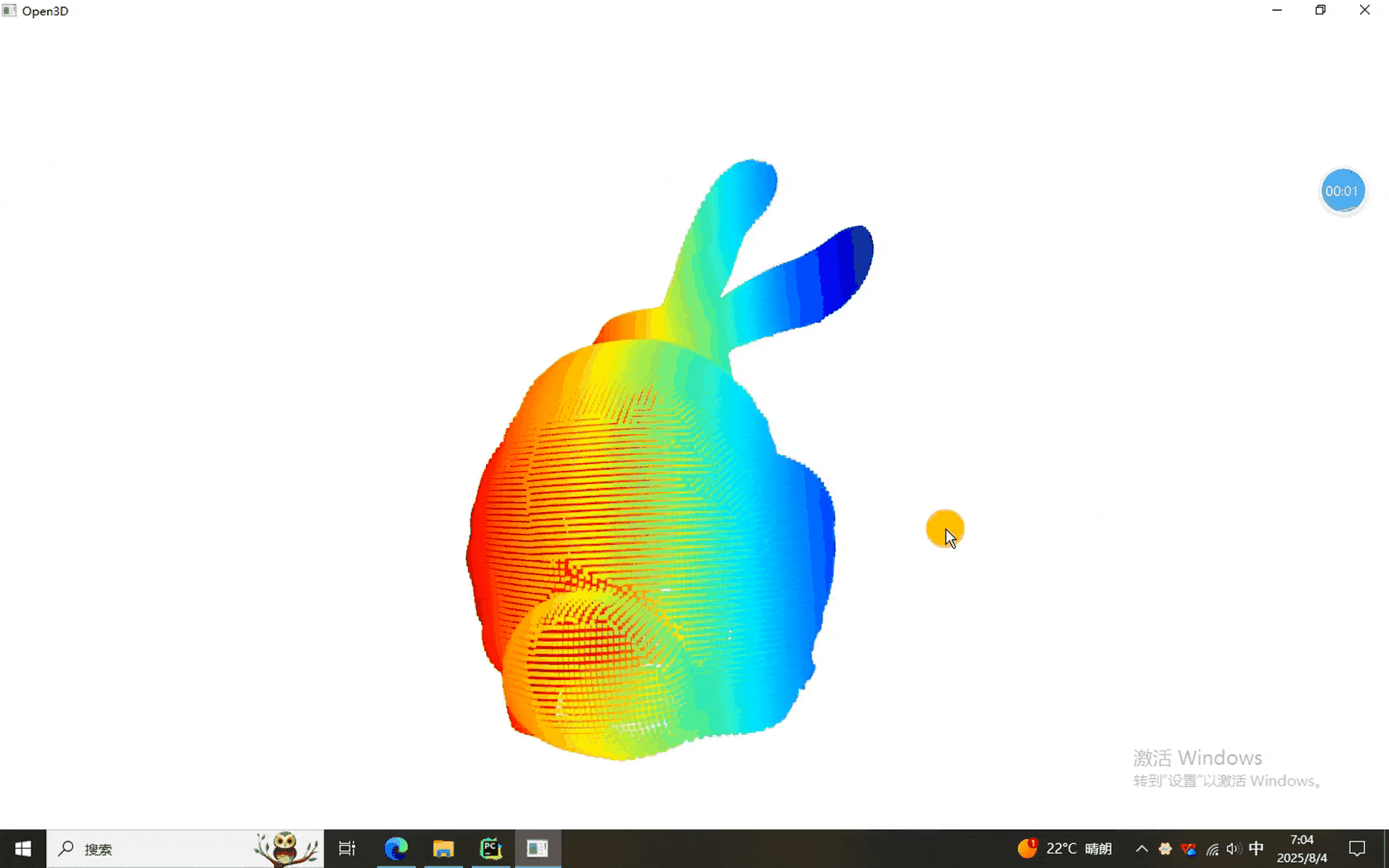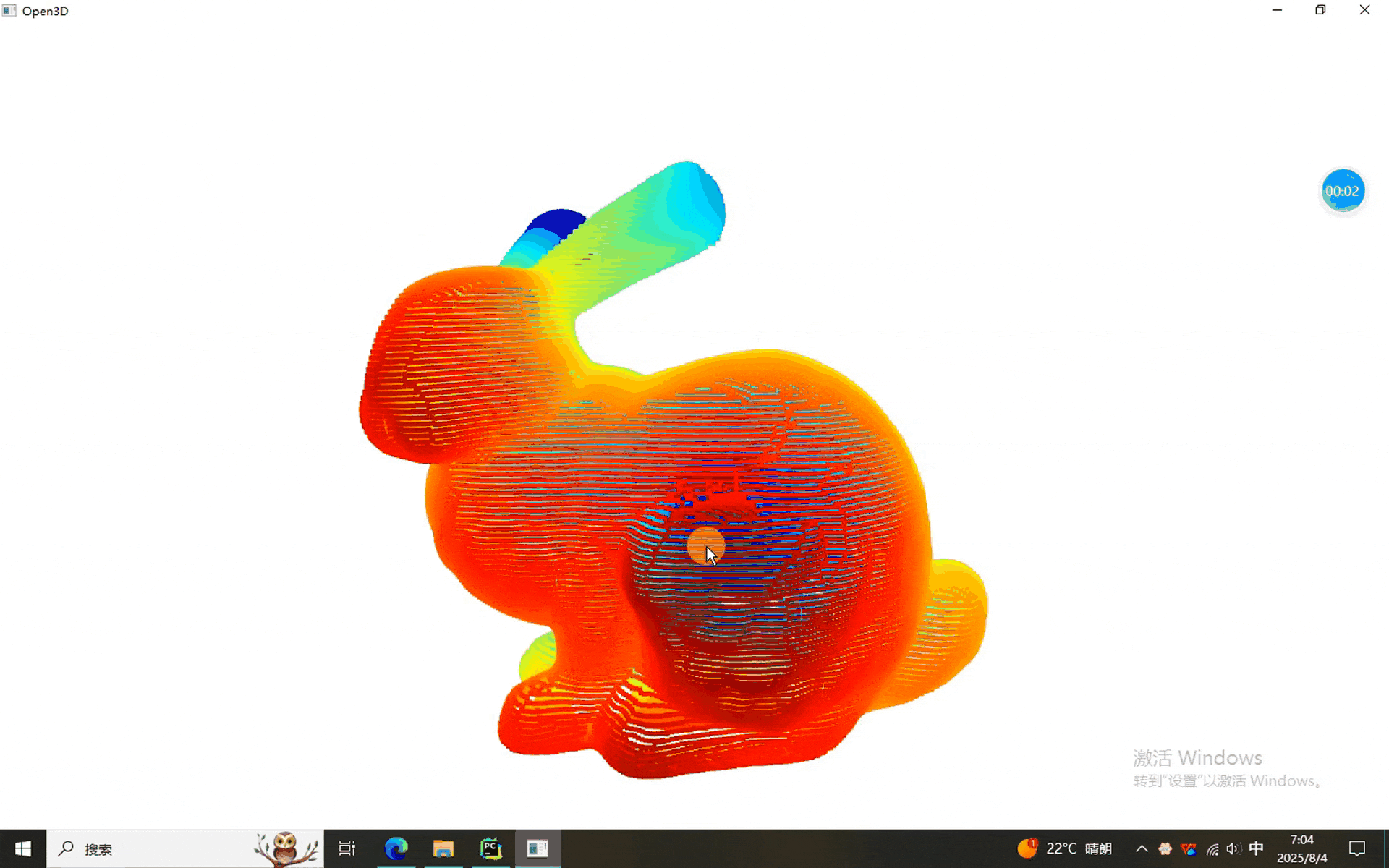
一、法向量定向程序
import tkinter as tk
from tkinter import messagebox
import open3d as o3d
import numpy as np
import threading
import os# ---------- 你的原函數,僅把輸入 pcd 改為深拷貝 ----------
def estimate_normals_by_center(pcd, knn_num=30, distance_threshold=0.001, outdoor=True):def is_normal_outward(normal, center):return np.dot(normal, center) > 0# 深拷貝pcd_1 = o3d.geometry.PointCloud()pcd_1.points = o3d.utility.Vector3dVector(np.asarray(pcd.points))point = np.asarray(pcd_1.points)center = np.mean(point, axis=0)point_size = point.shape[0]tree = o3d.geometry.KDTreeFlann(pcd_1)normals = []for i in range(point_size):[_, idx, _] = tree.search_knn_vector_3d(point[i], knn_num + 1)keypoint = pcd_1.select_by_index(idx)plane_model, inliers = keypoint.segment_plane(distance_threshold=distance_threshold,ransac_n=knn_num,num_iterations=10 * knn_num * knn_num)[a, b, c, d] = plane_modelnormal = np.array([a, b, c])if outdoor:normal = normal if is_normal_outward(normal, center) else -normalelse:normal = -normal if is_normal_outward(normal, center) else normalnormals.append(normal)pcd_1.normals = o3d.utility.Vector3dVector(np.array(normals))return pcd_1# ---------- 基礎可視化 ----------
def show(pcd, title=""):def run():vis = o3d.visualization.Visualizer()vis.create_window(window_name=title, width=1024, height=768,left=50, top=50)vis.add_geometry(pcd)render_option = vis.get_render_option()render_option.point_color_option = o3d.visualization.PointColorOption.Colorrender_option.point_size = 2.0render_option.show_coordinate_frame = Falsevis.run()vis.destroy_window()threading.Thread(target=run, daemon=True).start()# ---------- 讀取點云 ----------
FILE_NAME = "E:/CSDN/規則點云/bunny.pcd"
if not os.path.exists(FILE_NAME):messagebox.showerror("錯誤", f"請將 {FILE_NAME} 放在本腳本同級目錄!")raise SystemExit(1)base_pcd = o3d.io.read_point_cloud(FILE_NAME)
base_pcd.paint_uniform_color([1, 0, 0]) # 紅色
# 先統一計算一次法向量,后面只改變方向
base_pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.01, max_nn=30))# ---------- 4 種定向 ----------
def orient_minus_x():pcd = o3d.geometry.PointCloud(base_pcd)pcd.orient_normals_to_align_with_direction([-1, 0, 0])o3d.visualization.draw_geometries([pcd], point_show_normal=True, window_name="法向量朝向 -X",width=1024, height=768,left=50, top=50,mesh_show_back_face=False)def orient_camera():pcd = o3d.geometry.PointCloud(base_pcd)pcd.orient_normals_towards_camera_location([0, 0, 0])o3d.visualization.draw_geometries([pcd], point_show_normal=True, window_name="法向量朝向相機",width=1024, height=768,left=50, top=50,mesh_show_back_face=False)def orient_mst():pcd = o3d.geometry.PointCloud(base_pcd)pcd.orient_normals_consistent_tangent_plane(10)o3d.visualization.draw_geometries([pcd], point_show_normal=True, window_name="法向量最小生成樹一致",width=1024, height=768,left=50, top=50,mesh_show_back_face=False)def orient_center_outward():pcd = estimate_normals_by_center(base_pcd, outdoor=True)o3d.visualization.draw_geometries([pcd], point_show_normal=True, window_name="法向量朝向質心外側",width=1024, height=768,left=50, top=50,mesh_show_back_face=False)# ---------- Tkinter GUI ----------
root = tk.Tk()
root.title("點云法向量定向")
root.geometry("300x280")
tk.Label(root, text="選擇法向量定向方式", font=("微軟雅黑", 14)).pack(pady=10)btn1 = tk.Button(root, text="1 朝向 -X 方向", width=25, command=orient_minus_x)
btn2 = tk.Button(root, text="2 朝向相機位置", width=25, command=orient_camera)
btn3 = tk.Button(root, text="3 最小生成樹一致", width=25, command=orient_mst)
btn4 = tk.Button(root, text="4 質心外側方向", width=25, command=orient_center_outward)
btn5 = tk.Button(root, text="5 退出", width=25, command=root.quit)for b in (btn1, btn2, btn3, btn4, btn5):b.pack(pady=6)root.mainloop()二、法向量定向結果
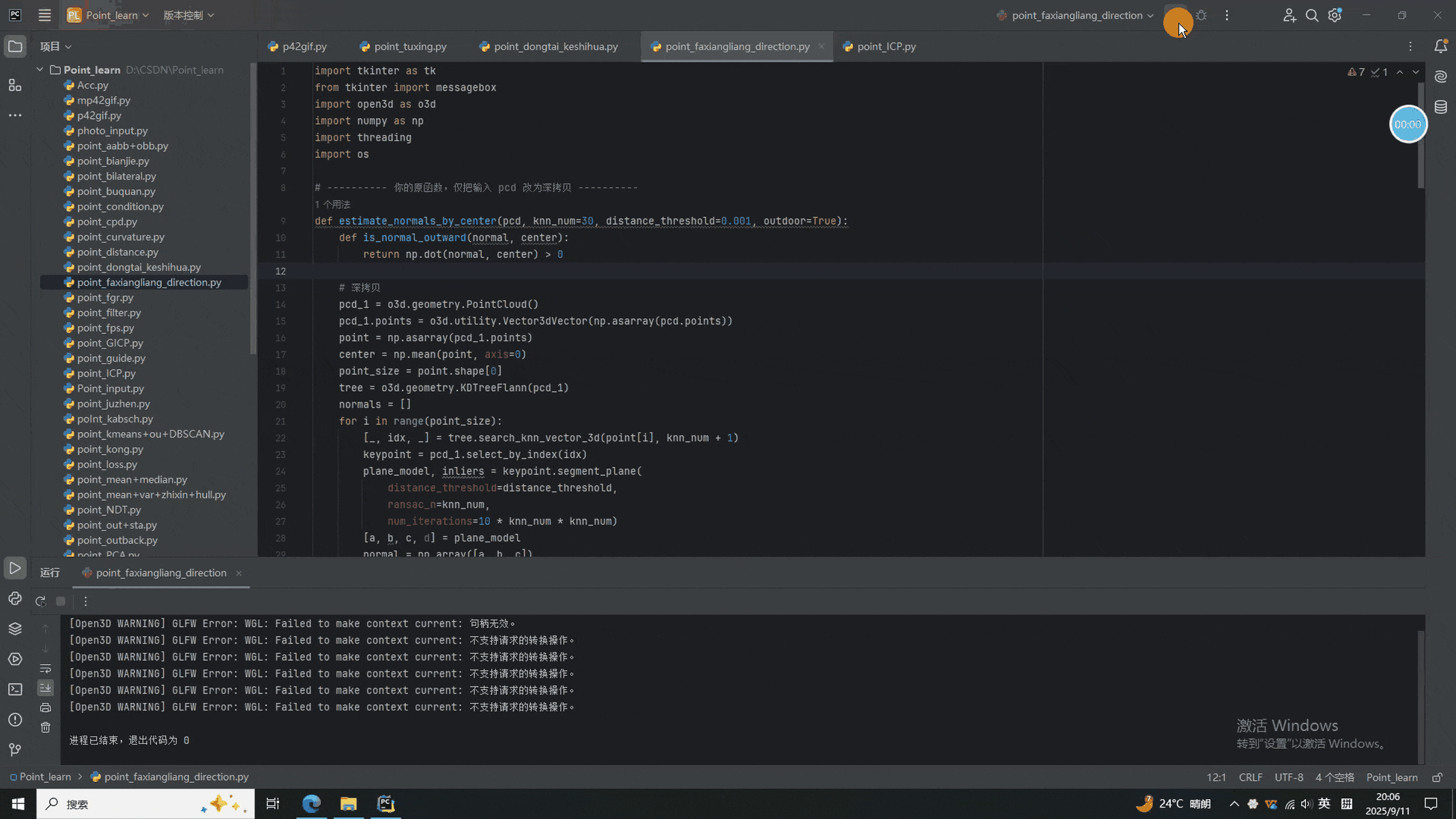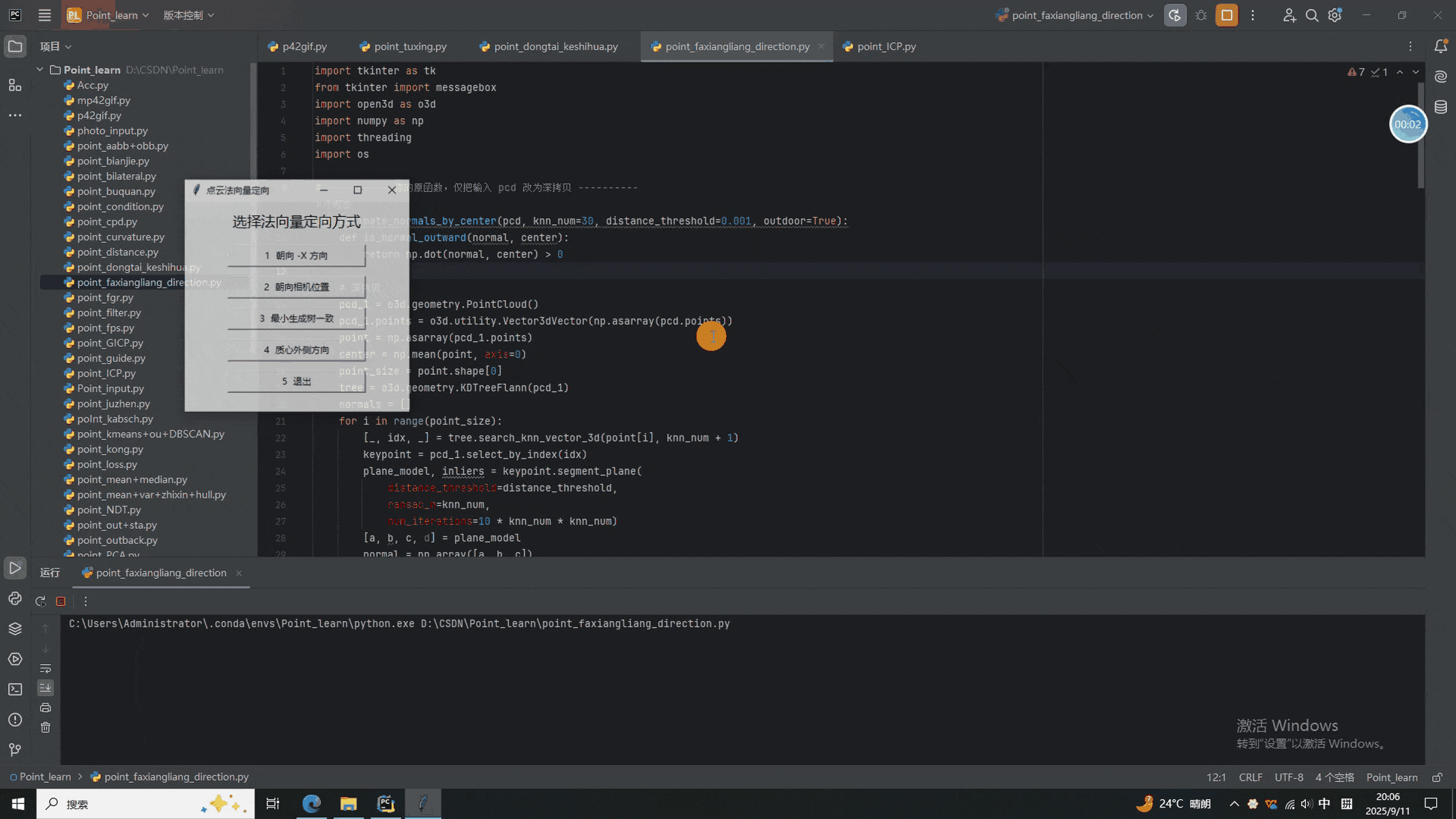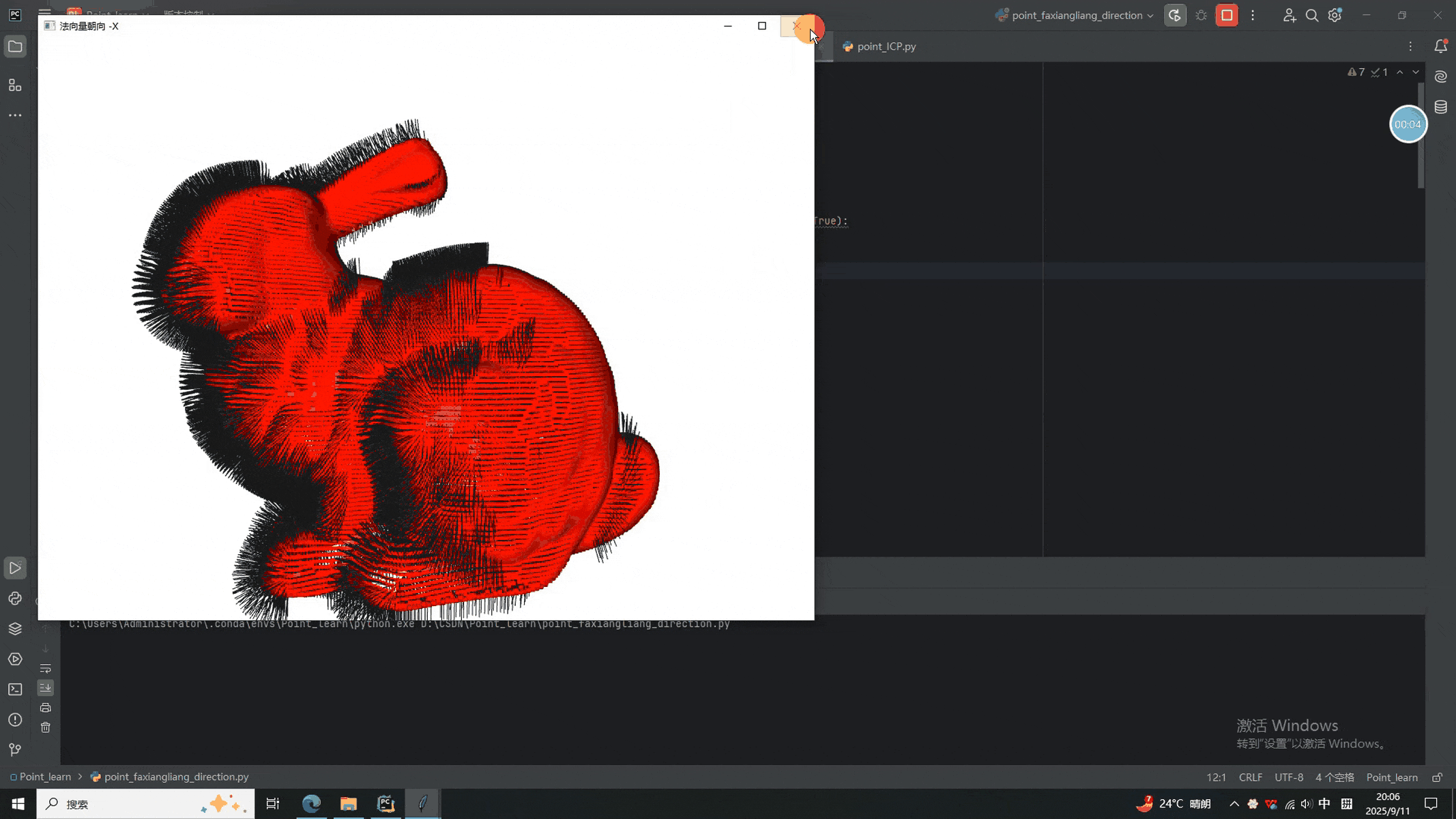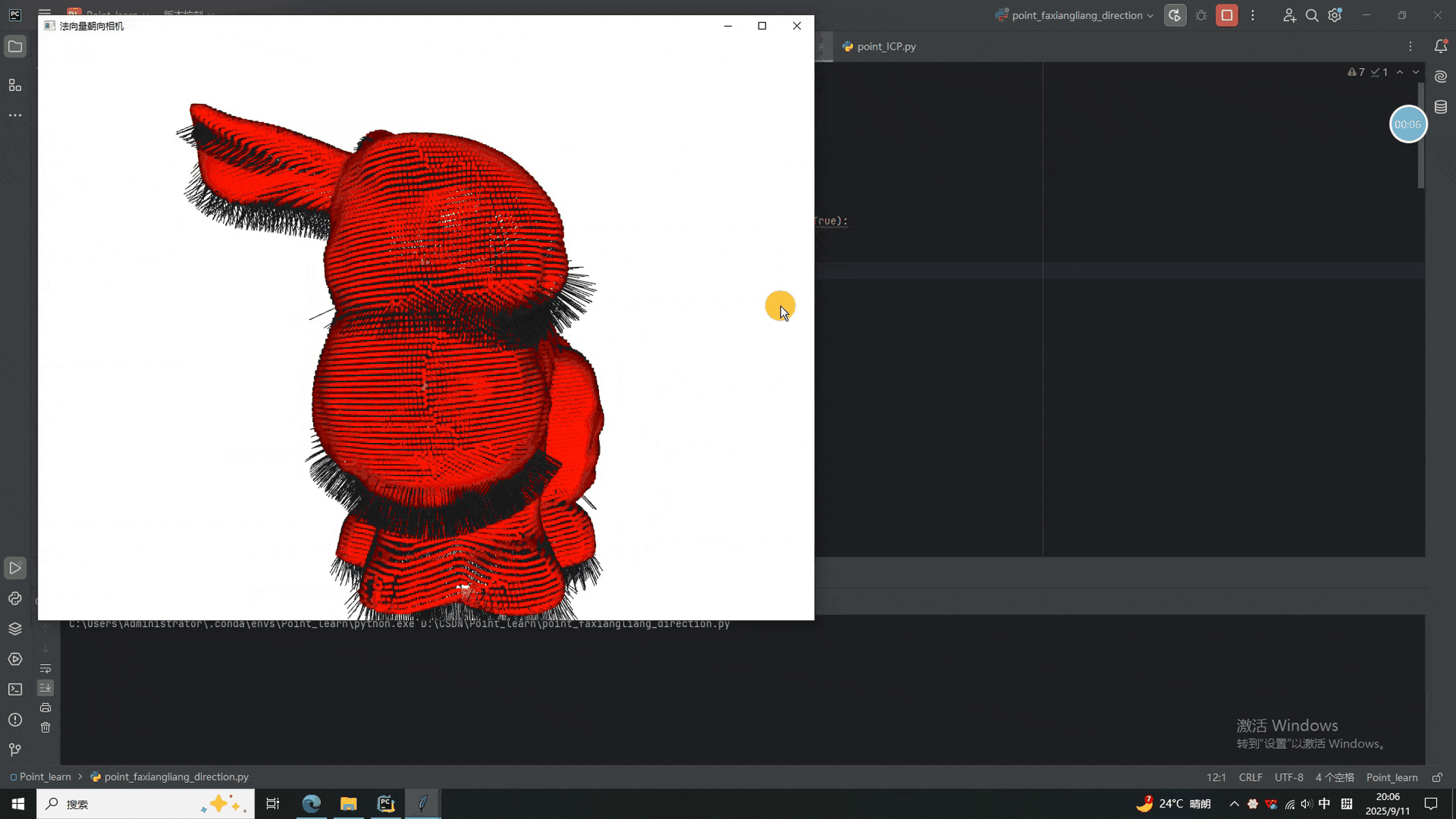
????????本次我們依然沿用前幾次的GUI界面(主要好用啊)。從結果中可以看出,使用不同的方法得到的法向量方向不一致(時間限制,只演示了前倆),如果要實際使用,還需要結合具體場景確定。同學們有興趣的一塊試試吧。就醬,下次見^-^








)




 Pod入門與實戰)





