https://www.lamda.nju.edu.cn/aml24fall/slides/Chap10.pptx
目錄
1.MDS (Multiple Dimensional Scaling) 多維縮放方法
2.?主成分分析 (Principal Component Analysis, PCA)
2.1 凸優化證明
2.2 人臉識別降維應用
3. 核化PCA
4. 流行學習
4.1 LLE 局部線性嵌入(Locally Linear Embedding)?
4.2?Isomap(等距特征映射)
5.?距離度量學習 (distance metric learning)
5.1 馬氏距離 度量矩陣M
5.2?近鄰成分分析 NCA
5.3 LMNN:Large Margin Nearest Neighbors
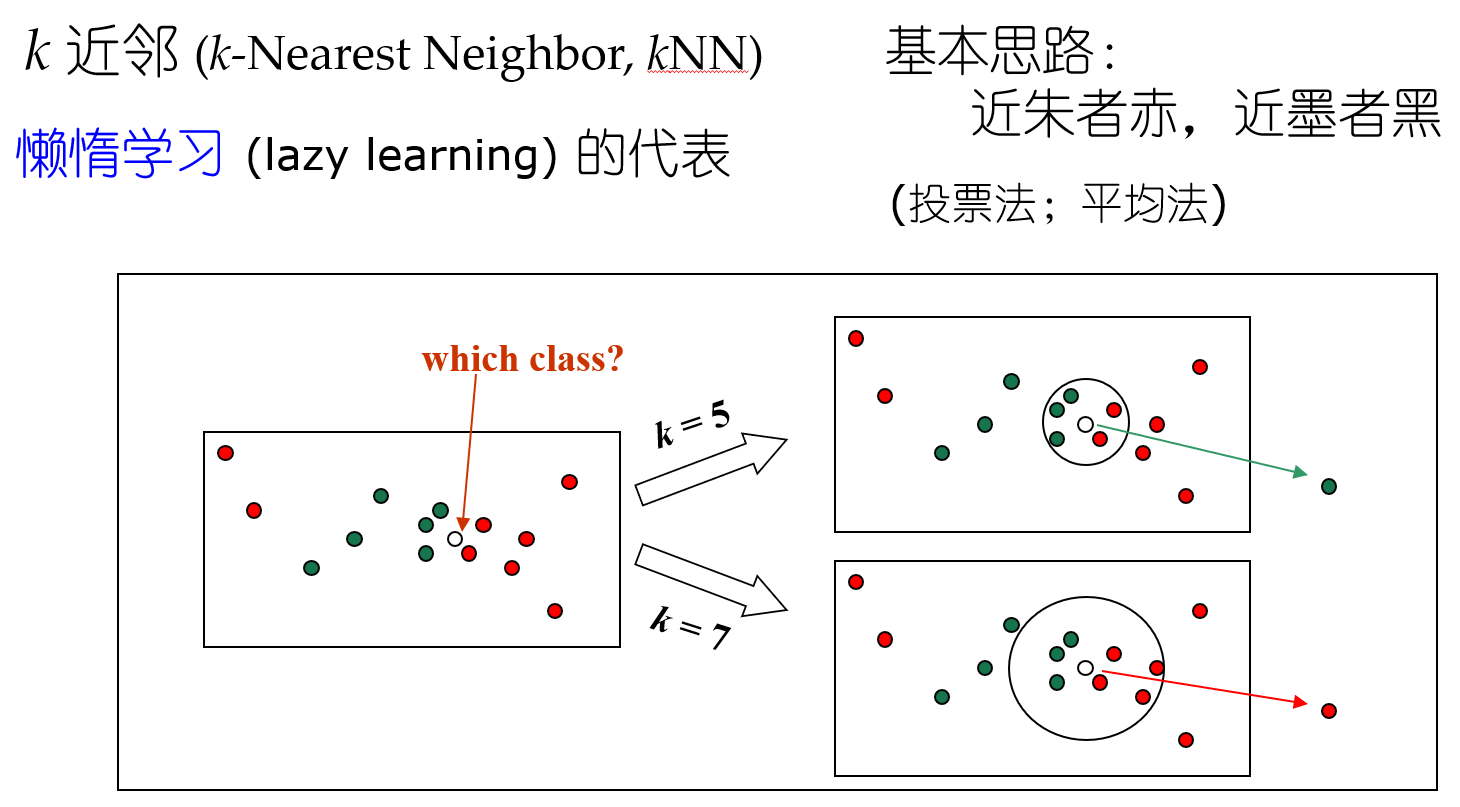
聚類 近朱者赤近墨者黑? ? ?kNN k的選取(參數影響結果 參數敏感性)+ 距離計算
密采樣(dense sampling) 高維維度爆炸
如果近鄰的距離閾值設為10^-3,
假定維度為20,如果樣本需要滿足密采樣條件,需要的樣本數量近10^60。
高維距離計算困難 內積都很困難,所以需要降維。
人是三維生物 但我們說要去某個地理位置 就說二維位置。(數據本身暗含低維假設 數據冗余)
打蚊子降維;? 梵高的畫流形(非線性) 畢加索的畫分段線性
1.MDS (Multiple Dimensional Scaling) 多維縮放方法
旨在尋找一個低維子空間,樣本在此子空間內的距離和樣本原有距離盡量保持不變。
線性降維:矩陣乘法。
變形問題:如何在低維子空間和高維空間之間保持樣本之間的內積不變?后續證明 保內積<=>保距離。
設樣本之間的內積矩陣均為B? 對B進行特征值分解:![]()
![]() ? ? ?
? ? ?![]()
譜分布長尾:存在相當數量的小特征值 ; 只保留前幾個大維度特征。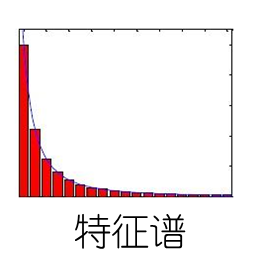
內積可以求取距離?![]()
距離矩陣D 可以求取內積矩陣B.? 所以保內積 等價 保距離不變。
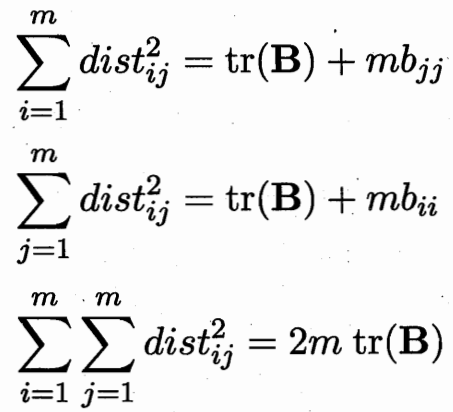 ??
??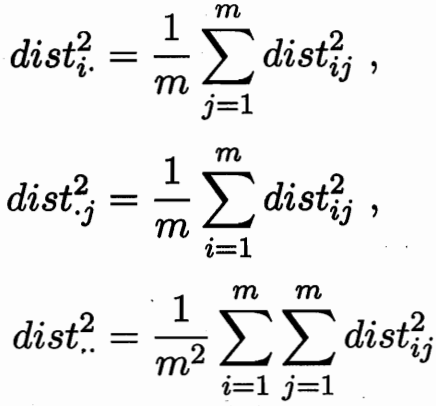
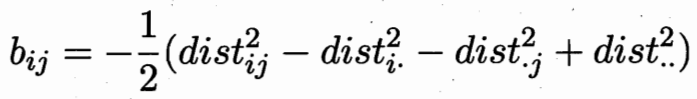
2.?主成分分析 (Principal Component Analysis, PCA)
正交屬性空間中的樣本點,如何使用一個超平面對所有樣本進行恰當的表達?
把散點拍到一個平面? ??主成分分析的兩種等價推導:最近重構性 與 最大可分性
1. 最近重構性:樣本點到這個超平面的距離都足夠近(平面擬合這些點 都很近)
樣本中心化 + 標準正交基??![]()
3i+4j+5k = (3,4,5)·(i,j,k) 內積? ? 如何得到3?? 和i做內積即可。 某方向的投影,即和那個方向的基做內積。
![]()
 ? ?w空間下的z 反推x,各個分量加起來。
? ?w空間下的z 反推x,各個分量加起來。

最小化這個跡 并基正交,可以轉化為優化問題? 是一個QCQP問題
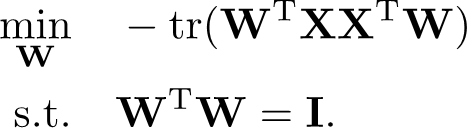
拉格朗日乘子法可得? ??![]()
2. 最大可分性:樣本點在這個超平面上的投影能盡可能分開
保持樣本本身的特性 -- 保留樣本和其他樣本的差異性? ? 下式和上式相同

2.1 凸優化證明
利用對稱矩陣乘上 W^T W 求導 -> 2W

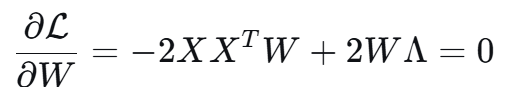 ?
?![]()
![]()
2.2 人臉識別降維應用
選取特征基,臉的空間中的基 還是臉; 被稱為特征臉eigenface?

黑白深淺表示某個局部識別的權重比例 比如第一張圖表示頭發權重很高,第四張圖表示胡子權重很高
3. 核化PCA



4. 流行學習
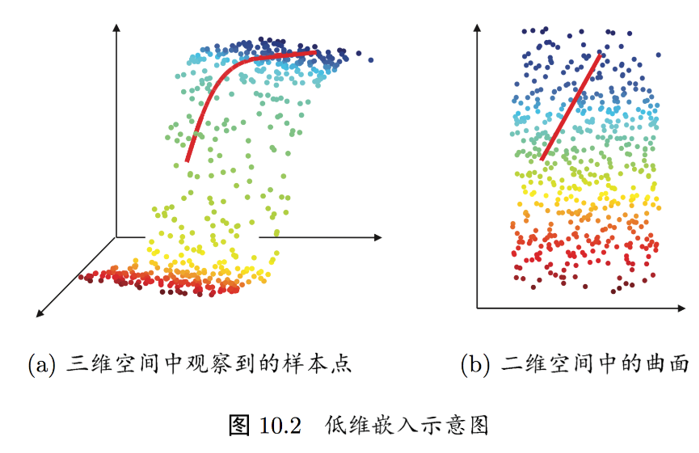
? ? ? ?若低維流形嵌入到高維空間中,則數據樣本在高維空間的分布雖然看上去非常復雜, 但在局部上仍具有歐氏空間的性質,因此,可以容易地在局部建立降維映射關系,然后再設法將局部映射關系推廣到全局。
可以類比成:世界地圖與地球儀? ?想象一下我們的地球。
-
高維空間(真實世界):地球本身是一個三維的球體(一個嵌入在三維空間中的二維流形)。你站在上面能感覺到它的弧度,這是一個復雜的曲面。
-
低維流形:但我們平時使用的世界地圖,是一張二維的紙。這張紙就是一個二維的表示。
-
局部具有歐氏空間性質:雖然整個地球是彎曲的,但你在你家小區、甚至整個城市范圍里活動時,你完全可以把地面當成是平的。在這個“局部”范圍內,東西南北、距離長短的規則(即歐幾里得幾何法則)都是成立的。這就叫“局部上仍具有歐氏空間的性質”。
-
在局部建立降維映射:制圖師如何繪制地圖呢?他們不會一下子畫整個地球。而是會一小塊一小塊地(比如先畫一個城市,再畫一個省)進行測繪。在每一小塊區域內,因為他們可以把地面當成平的,所以可以非常準確地將三維地形映射到二維紙上。這個過程就是“在局部建立降維映射關系”。
-
將局部關系推廣到全局:最后,制圖師需要把所有這些小塊的、平整的地圖,用某種方法(比如各種地圖投影算法)拼接、縫合起來,形成一張完整的、但必然有某種失真(比如格陵蘭島看起來和非洲一樣大)的世界地圖。這就是“設法將局部映射關系推廣到全局”。
4.1 LLE 局部線性嵌入(Locally Linear Embedding)?
低維空間 保留近鄰關系 + 近鄰權重 ;
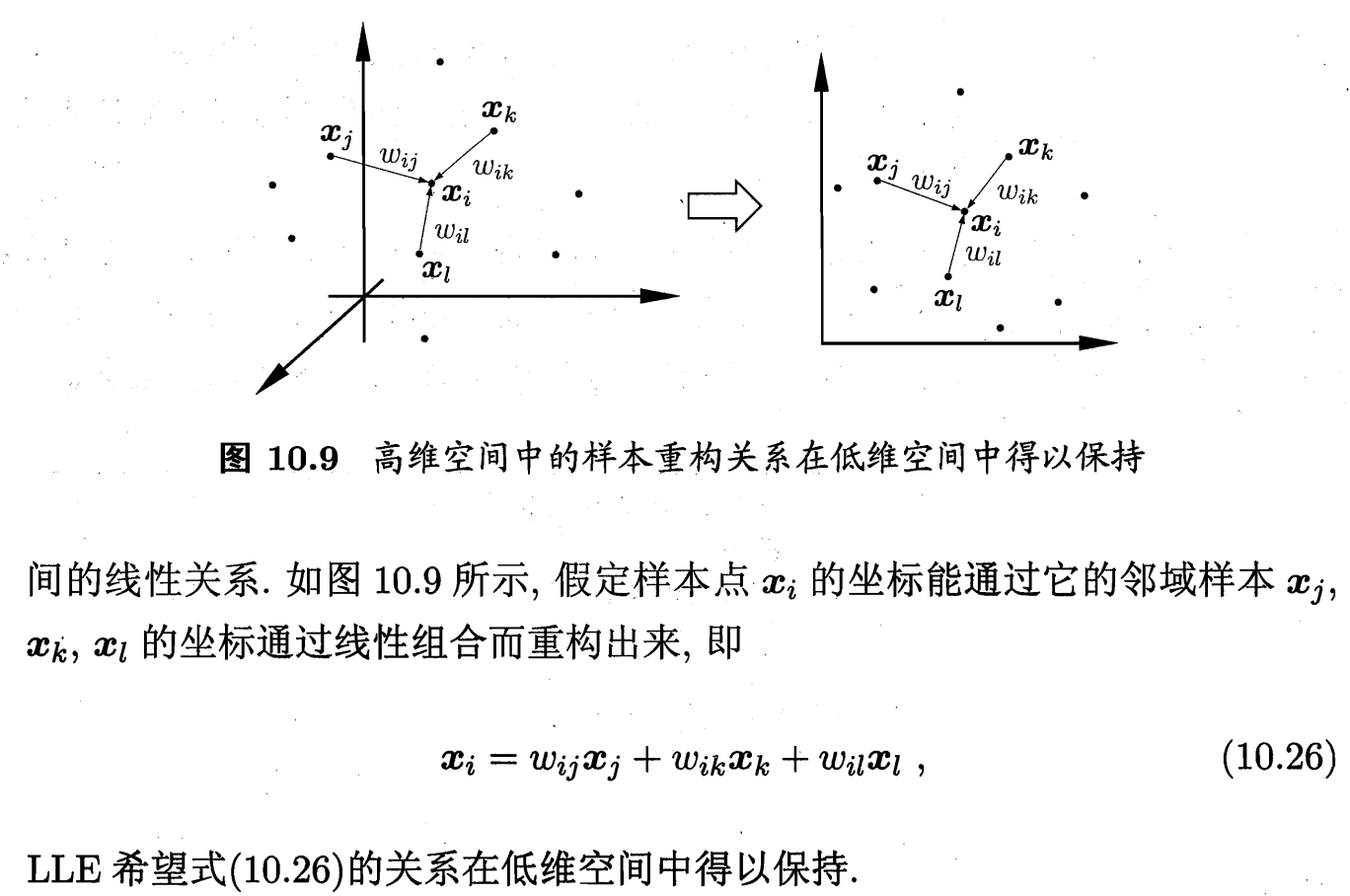
每個數據點都可以由其最近鄰的若干個點的線性組合來重構;
第一步:使用 K-NN(K近鄰)或 ε-球 的方法找到它的 k 個最近鄰點
第二步:計算局部線性關系的權重矩陣 我們試圖用它的 k 個近鄰點 x_j 來最佳地重構它自己。即,找到一組權重系數 W_ij,使得重構誤差最小化
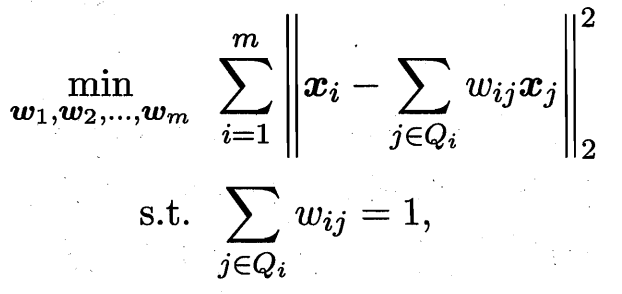 ? ??
? ??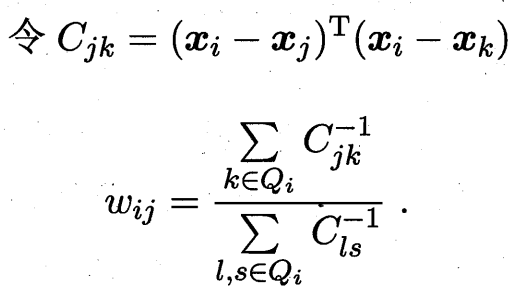
第三步:尋找一組低維表示 y_i 使得第二步中計算出的權重 W_ij 仍然能最好地重構 y_i
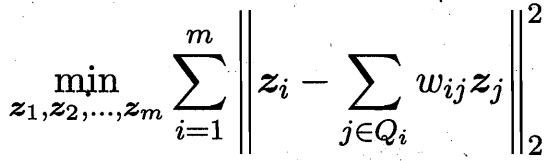
4.2?Isomap(等距特征映射)
測地距離才真實:數據點之間的真實相似性應該用流形上兩點之間的最短路徑(測地距離)來度量。
瑞士卷展平:理想情況沿著曲面走一圈;保距保的是 展開后平面的距離
飛機兩城市飛行軌跡:不只是直接走圓弧 而是要求走的路徑經過有機場的城市(失事著陸)
選取一些點 把這些點兩兩連起來 形成路線 (有點像無向圖單源最短路)
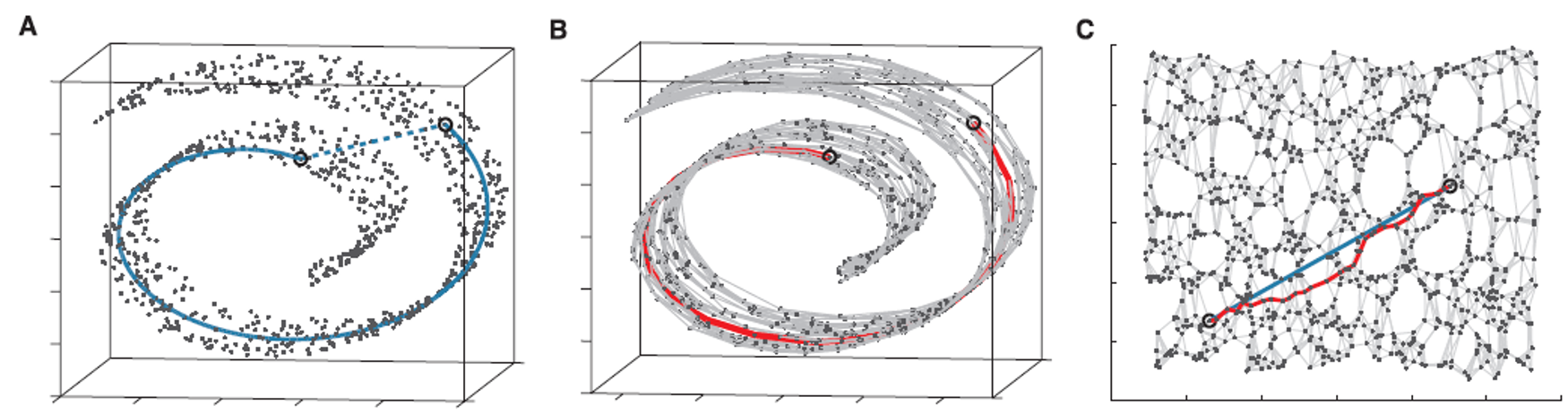
第一步:使用 K-NN(K近鄰)或 ε-球 的方法找到它的 k 個最近鄰點
第二步:基于最短路徑算法 近似任意兩點之間的測地線(geodesic)距離
第三步:尋找一個低維表示,使得在低維空間中點與點之間的歐氏距離,盡可能地接近第一步中計算出的測地距離矩陣 D_G
5.?距離度量學習 (distance metric learning)
降維的主要目的是希望找到一個“合適的”低維空間,在那個空間再算歐氏距離。
能否根據data的類別 直接“學出”合適的距離?
核心思想: 讓機器從數據中自動學習一個最優的距離度量函數,而不是手動選擇。
5.1 馬氏距離 度量矩陣M
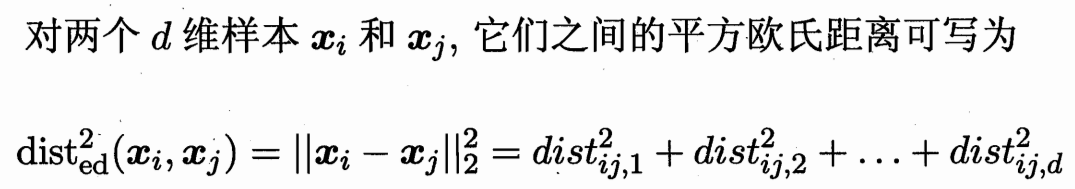
即兩個點之間 向量的長度的平方。(xi-xj)^T (xi-xj)
中間乘以一個對角陣 W 即進行不同維度的加權。
中間乘一個半正定對稱矩陣(為了保持距離非負且對稱)M(度量矩陣)
得到馬氏距離 (Mahalanobis distance)
![]()
若已知“必連”(must-link) 約束集合M? 目標函數最小化他們之間的距離,
與“勿連”(cannot-link) 約束集合C(最少也要距離1)因為沒有對M的尺度放縮限制條件 設置一個常數。
則可轉化為求解這個凸優化問題:
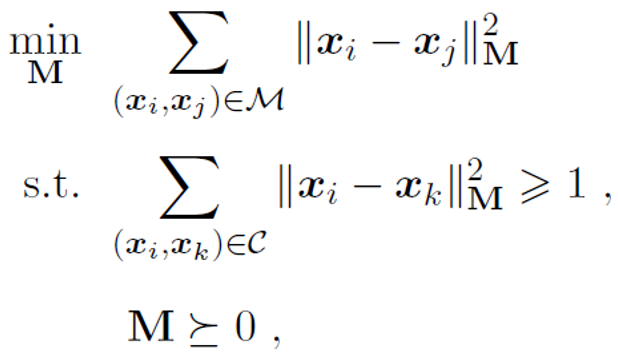
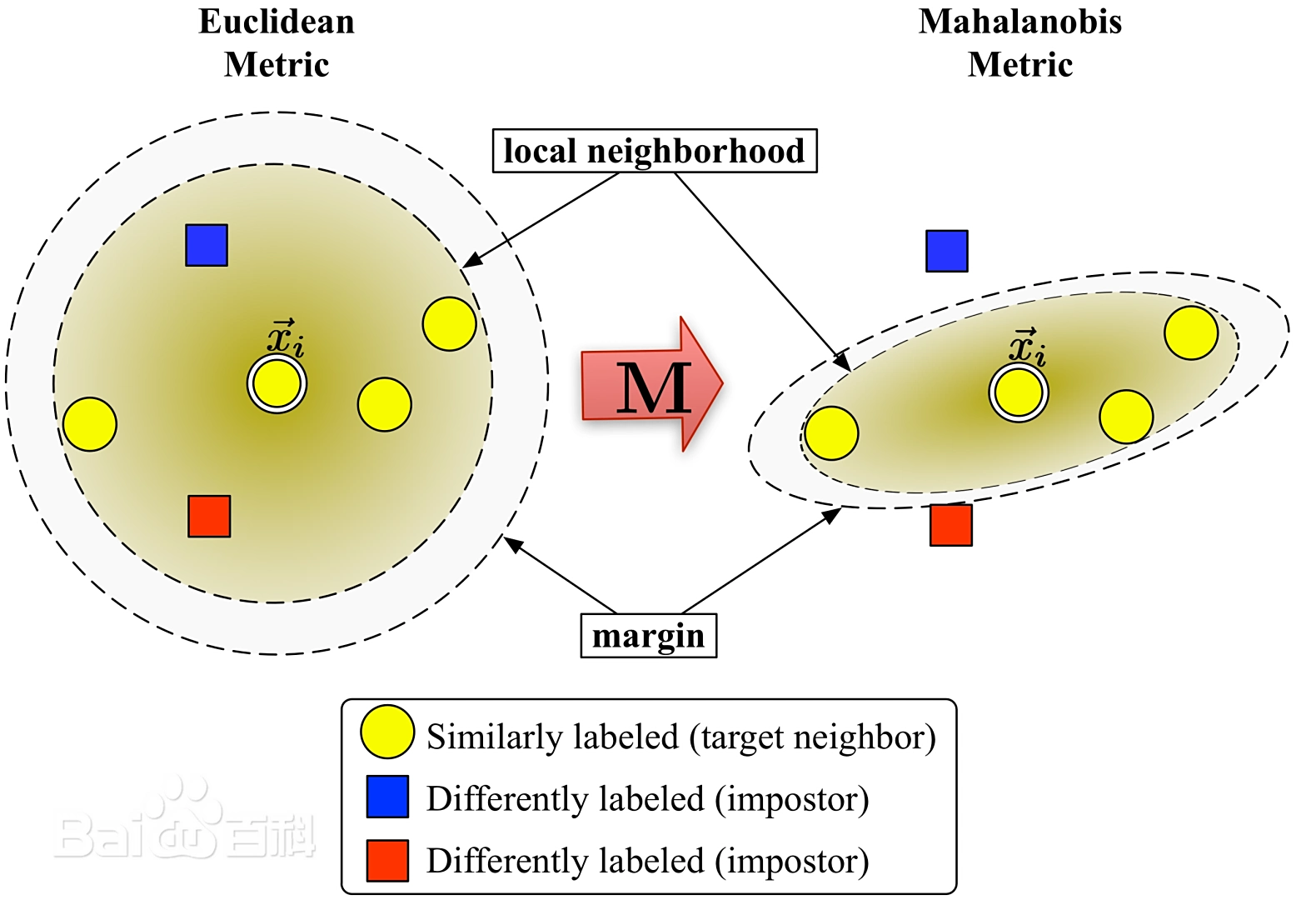
5.2?近鄰成分分析 NCA
近鄰成分分析(Neighbourhood Component Analysis,簡稱 NCA) (致敬PCA)
近鄰分類器在進行判別時通常使用多數投票法,鄰域中的每個樣本投1票, 鄰域外的樣本投0票。
不妨將其替換為概率投票法 j 對 i 投票的影響力,像softmax。
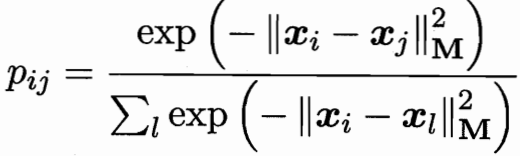
單個樣本即 各種j對i的投票和;整個訓練集 即所有樣本求和。

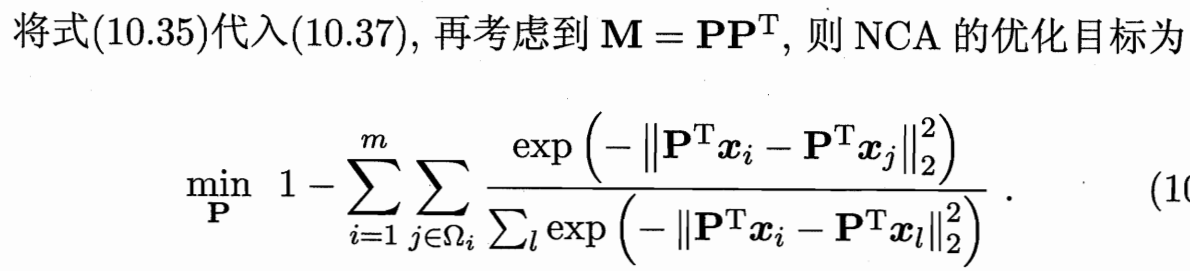
5.3 LMNN:Large Margin Nearest Neighbors
學習一個新的距離度量,使得在這個新的空間里,K-NN算法的性能達到最優。
臨近位置 相似標簽要盡量近 不同標簽盡量遠;至少要間隔margin 否則懲罰。
![]() ?拉近損失
?拉近損失
拉遠損失 差值是否>1 的一個0-1變量;寫在優化問題中 設置為ε
![]() ??
??
![]() ?加權一下
?加權一下
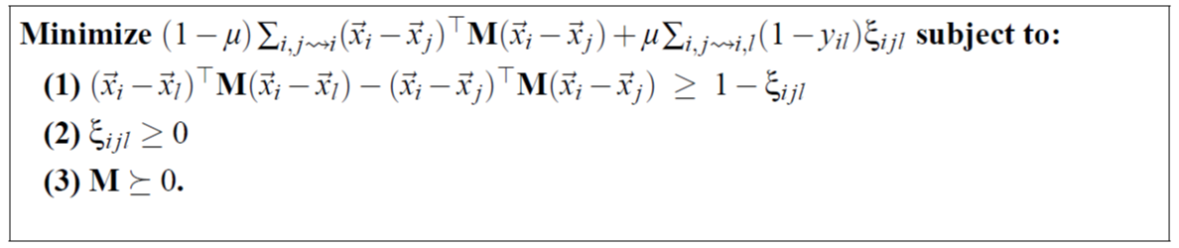
? 維度降下去了 丟掉了什么信息?丟掉了訓練的時候用的信息。
比如上面的 i,j,l 三元組訓練。抽取所有三元組 就是n^3級別 不算這么多,進行采樣,那么沒被采樣到的數據 相當于被丟掉了。




![第十四屆藍橋杯青少組C++選拔賽[2023.1.15]第二部分編程題(2 、尋寶石)](http://pic.xiahunao.cn/第十四屆藍橋杯青少組C++選拔賽[2023.1.15]第二部分編程題(2 、尋寶石))
+API 權威源 | 電影趨勢分析 / 推薦系統 / NLP 建模用)








:實現隊列/棧的利器,底層原理與實戰)




