單純形法的原理

先來舉個例子：
用單純形法求解下面線性規劃問題的最優解：

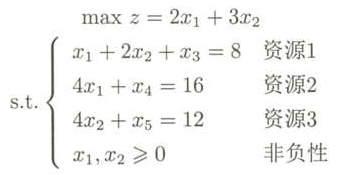
注釋：解的過程是反復迭代的過程，如果第一次迭代沒有理解也沒關系，再繼續看第二次迭代，和第三次迭代，每次迭代的流程都是一樣的，建議自己看完之后，再手寫一遍回憶一下哦~~

解析：

單純形法的原理

線性規劃問題的標準型如圖：

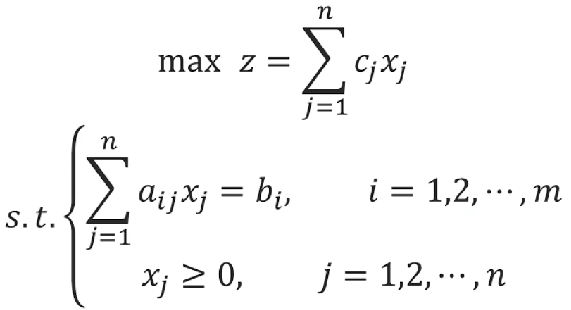
首先要得到一個初始的基可行解，具體做法如下：

假設系數矩陣A為下圖所示的情形：

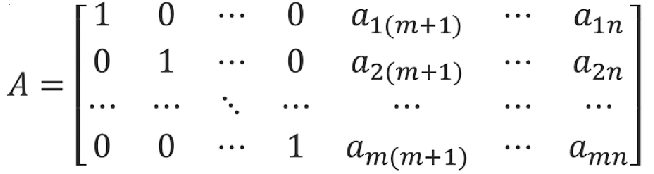
它的前m列就可以組成一個滿秩矩陣B，且有B=（P₁,P₂······P_m）=I
再將基變量用非基變量來表示：

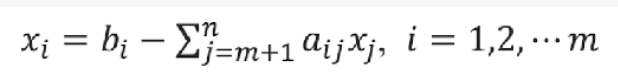
此時的目標函數里面的基變量也用非基變量表示：

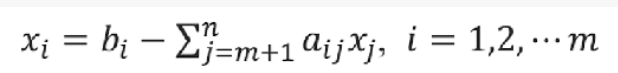
此時，令非基變量全部為0，就可以得到一個初始的基可行解：

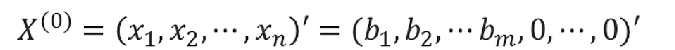
第二步就是判斷得到的基可行解是否是最優解，具體做法如下：

目標函數在此時就變為只含非基變量的形式：

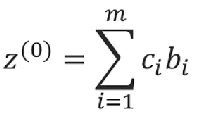
觀察目標函數中非基變量的系數:

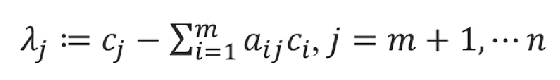
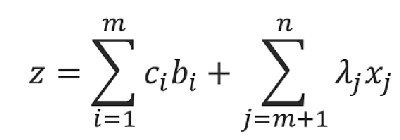
如果從λ_m+1一直到λ_n中只要有一個系數是正的，那么就說明當前的基可行解不是最優解，需要進一步改進目標函數的值，只有一直改到所有非基變量的系數全部為負時才說明那個時刻的基可行解是最優解。
因為用λ_i來判斷最優解的情況，所以λ_i就被稱為是檢驗系數。

第三步的改進就是更改基變量，然后迭代出新的目標函數，得到新的基可行解。具體的方法仍然是先比較目標函數中非基變量中的系數，選擇系數最大的變量作為入基，然后接著上述步驟來繼續進行迭代改變目標函數。
單純形法的基本步驟總結：

定理1

對基可行解，如所有的檢驗系數λ_k≤0，k=m+1······n,那么X^(0)就是線性規劃問題的最優解。
因為只有非基變量都是≤0的情況時，此時Z才能獲得最大值。
（如果隨以上步驟理解的話，這個定理就很明顯了。
）

定理2

若某一個非基變量x_k的檢驗系數為正，對應的列向量P_k=（a_1k,a_2k,······a_mk）所有的元素為非正，那么線性規劃問題就沒有最優解。

這個定理可以來判斷無界解。

單純形表

單純形表的布局方式：

具體的計算步驟如下：

舉個例子：
就以這篇文章開頭的例子為題，用單純形表來解的步驟如下：

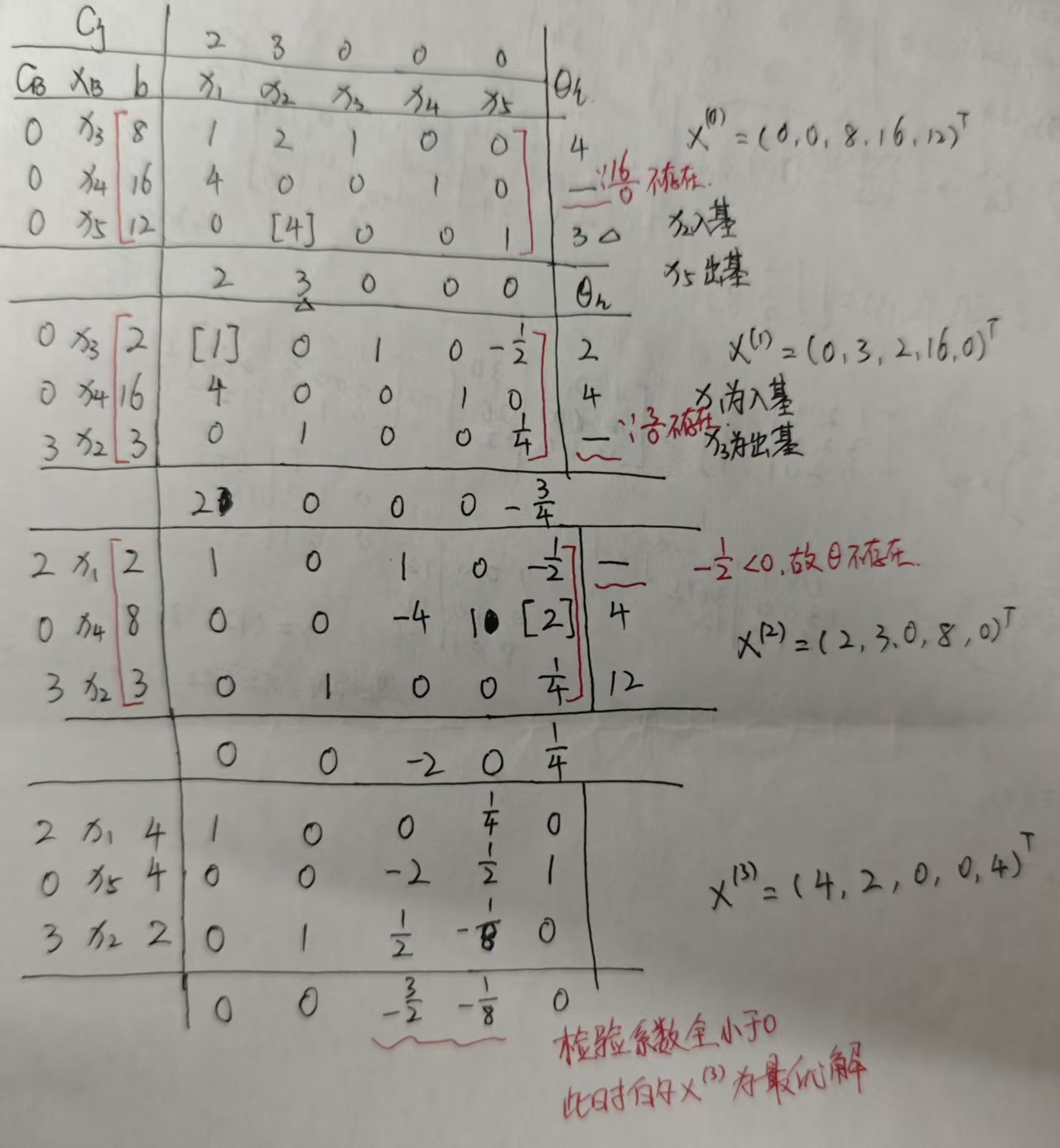
在第一個表中，只是將初始的全部數據列出，需要計算的是最后一行檢驗系數和最后一列Θ_i的值.x₁所在列對應的檢驗值由公式：μ_i=c_i - ∑c_jx_i可得μ₁=2 -（01+04+00）=2，那么x₂所在列對應的檢驗值由公式就可得μ₂=3 -（02+04+0*4）=3，選出最大的項是x₂對應的3。
再計算最后一列Θ_i的值，第一行Θ_i的值：8?2=4，第二行Θ_i的值：16?0是不存在的，所以畫一條橫線，第三行Θ_i的值：12?4=3，選取Θ_i的值最小的數為3，所以具體就對應到中間系數矩陣的第三行，第二列的數值4，說明x₂為入基，x₄為出基，此時將4所在位置的這一列化為單位向量，也就是這一列化成（0,0,1）^T的形式。一定要以增廣矩陣為整體來做初等行變換。
一直到所有的檢驗系數都是負數時停止換基迭代，此時對應的z值就是：z=∑c_i??b。
每一步對應的基不同時，一定要記得變換，基的確定是在對增廣矩陣做初等行變換后才確定的