截止周四晚上11點已更新五個問題完整建模和問題一二的代碼
截止周五早上完整版已更新 可以看主頁最新博文獲取

完整內容請看文末最后的推廣群

2.1問題1的分析
問題1是典型的確定性時空幾何與運動學計算問題，核心在于通過建立坐標系下的參數方程，量化煙幕云團、導彈M1及真目標的時空位置關系，最終求解有效遮蔽的時間區間長度。該問題無需優化，僅需嚴格依據給定參數進行“事件鏈-位置計算-遮蔽判定”的閉環推導，所依賴的核心模型為運動學參數方程與空間幾何相交判定模型。
首先，構建統一的時間與空間基準模型。以雷達發現導彈時刻為t=0，基于笛卡爾坐標系（假目標為原點，z軸垂直于水平面），建立各主體的位置參數方程：
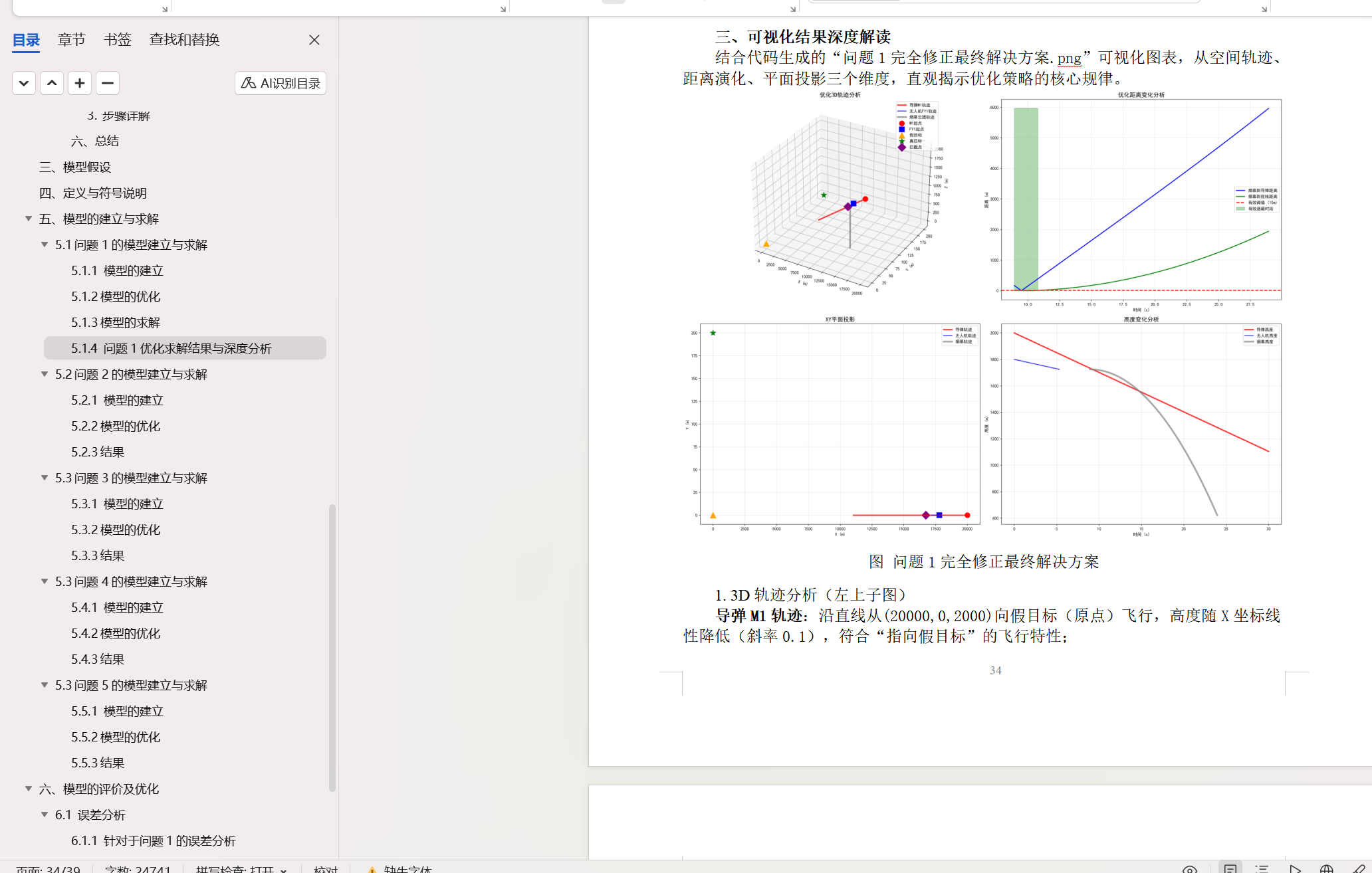
1.無人機FY1的位置方程：已知其沿x軸負方向（朝向假目標）以120 m/s勻速飛行，初始坐標(17800, 0, 1800)，則t時刻位置為。
2.導彈M1的位置方程：以300 m/s直指原點，初始坐標(20000, 0, 2000)，則t時刻位置為。
3.煙幕云團的位置方程：投放時刻s，投放點為；起爆延遲3.6 s，起爆時刻s，起爆后云團以3 m/s勻速下沉，故t≥5.1 s時云團中心坐標為，云團為半徑10 m的球體。
其次，明確有效遮蔽的判定模型。煙幕對M1的有效遮蔽需同時滿足時間約束與空間約束：
時間約束：起爆后20 s內，即。
空間約束：M1與真目標之間的視線線段需與煙幕云團球體相交。真目標為底面圓心(0,200,0)、半徑7 m、高10 m的圓柱，可簡化為點集。任取中一點，視線線段與球體有交點，則判定為有效遮蔽。
最后，通過線段與球體相交的解析算法求解約束條件。將視線線段參數化為（），代入球體方程得到關于s的二次方程，若方程在s∈[0,1]內有實根，則判定相交。遍歷真目標特征點（如圓心、邊緣點），求解滿足相交條件的t區間，區間長度即為有效遮蔽時長。該過程需通過MATLAB或Python實現數值求解，核心是將幾何判定轉化為代數方程的根的存在性問題。

2.2問題2的分析
問題2是單變量約束優化問題，目標函數為有效遮蔽時長，優化變量為FY1的飛行參數（方向θ、速度v）、投放時刻t0、起爆延遲Δt，核心是通過建立“變量-目標函數”的映射關系，結合約束條件尋找最優解，所依賴的模型為多變量優化模型與煙幕遮蔽效能評估模型。
首先，定義優化變量與約束集。設飛行方向θ為速度向量與x軸正方向的夾角，則FY1的速度分量為，t時刻位置為；投放時刻t0（t0≥0），投放點為；起爆延遲Δt（Δt≥0），起爆時刻，云團中心坐標為（t≥t1）。約束條件包括：，，（為M1到達真目標的時間，計算得約66.67 s）。
其次，構建目標函數模型。有效遮蔽時長是t的集合的測度。為簡化計算，采用真目標中心近似法，以真目標底面圓心代表真目標，此時視線線段為，目標函數可通過求解線段與球體相交的t區間長度直接量化。
最后，設計優化算法求解。由于變量維度較高（4維），采用分層優化策略結合粒子群優化（PSO）算法：
2.第一層：固定θ，將問題降為3維（v,t0,Δt）優化，通過PSO算法搜索該θ下的最優解；
3.第二層：遍歷θ∈[0,2π)，尋找全局最優θ及對應的v,t0*,Δt*。
優化過程中需通過數值迭代驗證每個粒子（變量組合）對應的遮蔽時長，核心是將優化算法與幾何相交判定模型耦合，確保目標函數計算的準確性。同時，為避免局部最優，需設置合理的PSO參數（種群規模、迭代次數、慣性權重），并通過多次隨機初始化種群提高解的全局最優性。
2.3問題3的分析
問題3是多彈時序協同優化問題，需在單無人機約束下（投放間隔≥1 s，飛行參數固定），通過優化3枚干擾彈的投放與起爆時序，實現遮蔽時長的疊加最大化，核心模型為多彈時序協同模型與整數規劃約束下的優化模型。
首先，建立多彈投放的時序約束模型。設3枚彈的投放時刻為t01、t02、t03，滿足，；起爆延遲為Δt1、Δt2、Δt3，起爆時刻為t11=t01+Δt1、t12=t02+Δt2、t13=t03+Δt3；各彈有效遮蔽時段為（i=1,2,3）。總有效遮蔽時長為3個區間的并集測度，即，目標是最大化。
其次，構建飛行參數與投放點的關聯模型。FY1飛行參數（θ,v）固定后，3枚彈的投放點為，起爆點云團中心在t時刻的坐標為。由于飛行參數固定，投放點的空間分布由t01、t02、t03唯一確定，因此優化變量可歸為（θ,v,t01,t02,t03,Δt1,Δt2,Δt3）。
最后，設計混合優化算法。考慮到變量維度高且含時序約束，采用遺傳算法（GA）+局部搜索的混合策略：
3.編碼：將θ、v、t01、t02、t03、Δt1、Δt2、Δt3編碼為染色體，其中θ采用角度編碼，v、t0i、Δti采用實數編碼；
4.適應度函數：計算每個染色體對應的，作為適應度值；
5.選擇、交叉、變異：采用輪盤賭選擇、算術交叉、高斯變異，確保種群多樣性；
6.局部搜索：對適應度前20%的個體，微調t0i和Δti，優化區間銜接效果，避免遮蔽空白。
同時，需嵌入約束處理機制：對違反投放間隔或時間上限（t13+20≤66.67）的個體，設置適應度懲罰值，確保解的可行性。通過該算法可求解出最優飛行參數與多彈時序，實現遮蔽時段的連續或部分重疊，最大化總時長。

2.4問題4的分析
問題4是多無人機協同優化問題，需為FY1、FY2、FY3分配遮蔽任務，優化各機飛行與投放參數，實現多彈遮蔽時段的全局最優銜接，核心模型為任務分配模型與多智能體協同優化模型。
首先，建立任務分配的聚類模型。基于M1的飛行時間軸，將遮蔽任務劃分為3個時段：早期（t∈[tA,tB]）、中期（t∈[tB,tC]）、后期（t∈[tC,tD]）。采用K-means聚類算法，以M1在不同時刻的位置為樣本，將其劃分為3類，對應3個任務時段。根據無人機初始位置與任務時段的距離匹配度（距離=無人機初始位置到任務時段M1平均位置的歐氏距離/最大速度），分配FY1（初始距M1最近）執行早期任務，FY2執行中期任務，FY3（初始距真目標最近）執行后期任務。
其次，構建多無人機參數優化模型。設第k架無人機（k=1,2,3對應FY1,FY2,FY3）的優化變量為（θk,vk,t0k,Δtk），約束條件為，，（t1k=t0k+Δtk）。目標函數為總遮蔽時長，需滿足時段銜接約束（δ≤1 s，確保無縫銜接）。
最后，采用分布式粒子群優化（DPSO）算法求解。將3架無人機視為3個粒子群，每個粒子群優化自身變量，通過信息交互（共享各機的t1k）協調時段銜接：
4.每個子群優化自身變量，計算局部適應度（自身遮蔽時長）；
5.全局通信層匯總各子群的t1k，計算全局適應度（總遮蔽時長）；
6.各子群根據全局適應度調整自身搜索方向，優先優化t0k和Δtk以滿足銜接約束。
該算法通過分布式計算降低復雜度，同時通過信息共享實現全局協同，避免各機獨立優化導致的遮蔽重疊浪費或空白。

2.5問題5的分析
問題5是多目標、多資源的復雜優化問題，需統籌5架無人機（每架至多3枚彈）對M1、M2、M3的干擾任務，核心模型為資源分配整數規劃模型與多目標優化模型。
首先，建立資源分配的整數規劃模型。設決策變量為（1≤k≤5，1≤j≤3），表示第k架無人機分配給第j枚導彈的干擾彈數量，滿足（每機至多3枚），（每枚導彈至少1枚彈干擾），。目標函數為最大化3枚導彈的總遮蔽時長（為第j枚導彈的遮蔽時長）。采用分支定界法求解該整數規劃，確定各機對各導彈的投彈數量分配方案。
其次，構建多導彈遮蔽的效能評估模型。對每枚導彈Mj，其位置方程為，其中（xMj0,yMj0,zMj0）為初始坐標，αj為Mj飛行方向與x軸的夾角（由初始位置指向原點計算得出）。每枚干擾彈對Mj的遮蔽判定同問題1，需獨立計算。
最后，采用多目標遺傳算法（MOGA） 求解全局優化問題。由于需同時優化5架無人機的飛行參數（θk,vk）、各枚彈的投放時刻（t0kj）與起爆延遲（Δtkj），變量維度極高，需通過以下策略簡化：
1.分層優化：先通過整數規劃確定，再針對每個（k,j）組合優化其參數；
2.多目標處理：將T1、T2、T3作為三個目標，采用非支配排序遺傳算法（NSGA-II）搜索帕累托最優解，最終根據實際需求（如優先保護真目標，可側重M1的遮蔽時長）選擇折中解。
同時，需考慮多導彈視線的干擾耦合：若一枚干擾彈同時處于多枚導彈的視線路徑上，可同時計入多枚導彈的遮蔽時長，通過該“協同增益”提升整體效能。算法實現中需通過并行計算加速多彈遮蔽判定，確保優化效率。