引言

歡迎來到本系列的第十一篇！在我們通過“最大深度”問題初步領略了樹的遞歸之美后，今天我們將面對一個更能體現遞歸“分治”思想的經典問題——LeetCode 226. 反轉二叉樹。

這道題在面試界的地位非同凡響，它因 Homebrew 的作者 Max Howell 在 Google 面試時被這道題難住，并憤然發推吐槽而聞名于世。但這道題真的那么難嗎？

當你第一次看到這道題，你可能會發現它具有一種“鏡像”的對稱性，并且可以分解成更小的、相同的問題。這正是解決它的正確方向！但如何將這種直覺轉化為清晰、正確的代碼呢？

本文將帶你一起：

1. 分析并完善關于“完全二叉樹”、“終止條件”等問題的初步想法。

2. 深入理解遞歸如何像一個“自上而下的命令鏈”，優雅地完成整棵樹的反轉。

3. 掌握解決這類樹結構修改問題的通用遞歸模板。

---

一、題目呈現

• 題目編號：226. 反轉二叉樹

• 題目難度：簡單

• 題目鏈接：226. 反轉二叉樹 - 力扣 (LeetCode)

• 題目描述：

  給你一棵二叉樹的根節點?root?，翻轉這棵二叉樹，并返回其根節點。

• 示例：

  • 輸入:?root = [4,2,7,1,3,6,9]

  • 輸出:?[4,7,2,9,6,3,1]

  反轉前：

        4/ \2   7/ \ / \1  3 6  9

反轉后：

      4/ \7   2/ \ / \9  6 3  1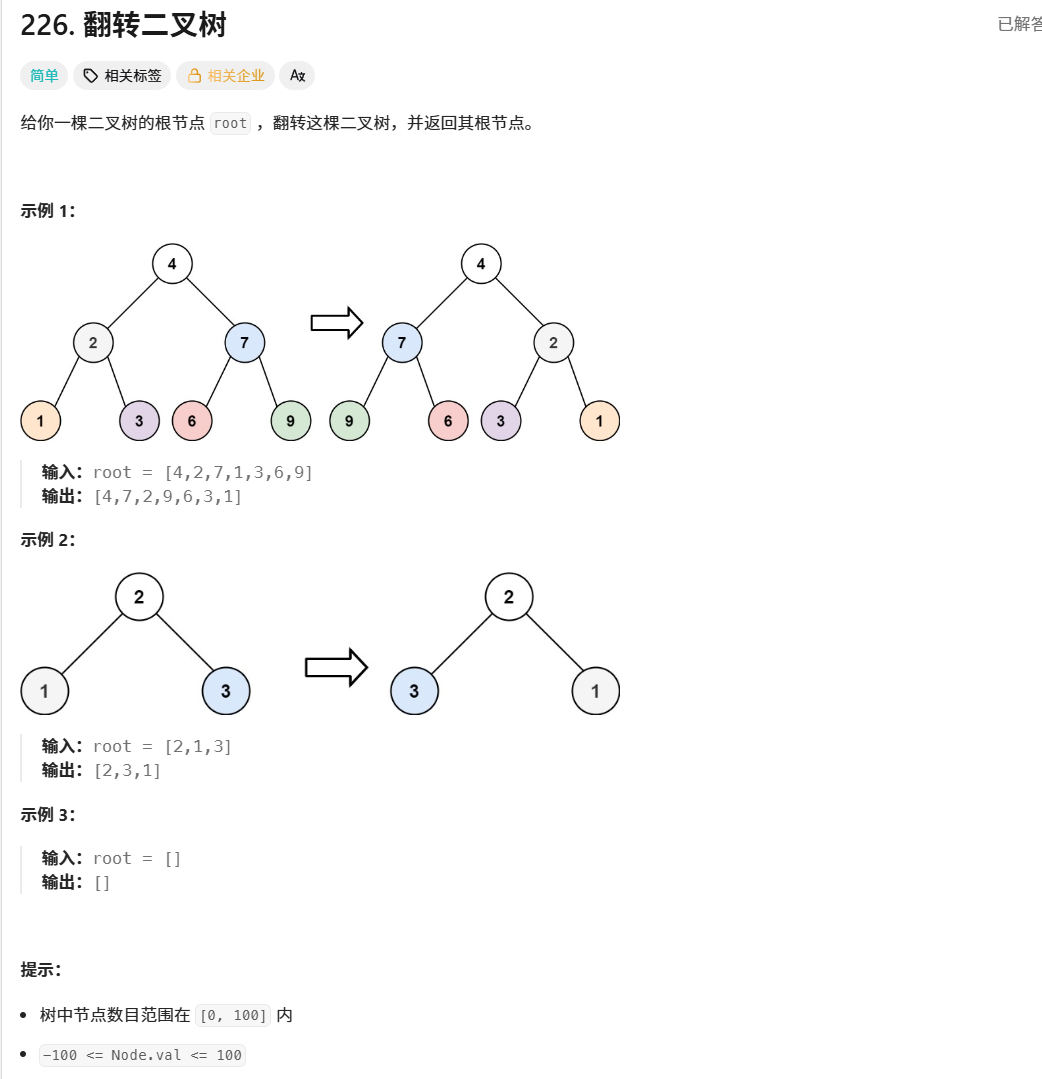

二、我的思考：遞歸直覺的打磨

（這里完全采用你的筆記思路）

看到這棵樹，我的第一反應是：這個問題可以拆分成更小的相同問題。比如，要反轉整棵以?4?為根的樹，似乎可以先反轉以?2?為根的左子樹，再反轉以?7?為根的右子樹，最后再做點什么。這種“分治”的感覺，讓我立刻想到了遞歸。

我的初步想法是：

1. 終止條件：當遞歸到最左邊的葉子節點，它的?left?是?nullptr?時，就應該停止了。

2. 核心操作：在某個節點，我需要交換它的?left?和?right?指針，這需要一個臨時變量來暫存。

但我很困惑：我應該按什么順序去遞歸呢？先一路遞歸到最左邊，再處理右邊嗎？那返回的順序好像不對。而且，函數最后應該返回什么？是節點的值?val?嗎？

你的思考過程非常棒！你已經抓住了遞歸和交換這兩個核心要素。現在，我們來逐一打磨這些想法，掃清困惑。

1. 關于終止條件：只考慮?left?為?nullptr?是不夠的。一個更通用、更安全的終止條件是：當遞歸遇到的當前節點?root?本身是?nullptr?時，就返回。因為我們不能對一個空節點做任何操作。

2. 關于返回值：函數的簽名是?TreeNode* invertTree(TreeNode* root)，它要求我們返回一個?TreeNode*?指針。我們的任務是修改樹的結構，并最終返回修改后整棵樹的根節點。

3. 關于遞歸順序：這正是本題的精髓！答案是，對于“反轉”這個操作，先處理當前節點，再遞歸子節點（前序遍歷）?的思路是最直觀的。

---

三、豁然開朗：遞歸的“自頂向下”反轉模型

讓我們把反轉過程想象成一個**“將軍下令”**的指揮鏈。

將軍（當前根節點?root）的任務只有兩件：

1. 先行動：交換自己直接指揮的兩個師長（左子節點?left?和右子節點?right）的位置。

2. 再下令：對換完位置的兩位師長分別說：“現在，你們各自去把手下的部隊（你們的子樹）也全部反轉一遍！”

這個命令會從最高級的將軍?root，一層層地傳遞下去，直到最底層的士兵（葉子節點）。當士兵接到命令，發現自己手下沒有兵（子節點為?nullptr）時，他什么也不做，直接報告“任務完成”。當所有士兵都報告完成后，整棵樹的“鏡像反轉”就完成了。

C++ 最優代碼與詳解

這個“將軍下令”的模型，可以被直接翻譯成極其簡潔的遞歸代碼。

完整代碼

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {// 1.if (root == nullptr) {return nullptr;}// --- 核心操作區 (前序遍歷位置) ---// 2.TreeNode* temp = root->left;root->left = root->right;root->right = temp;// 3.invertTree(root->left);invertTree(root->right);// 4.return root;}
};

代碼逐點解釋

1. if (root == nullptr)
   遞歸的終止條件 (Base Case)。如果當前節點為空，它沒有子節點可以交換，直接返回?nullptr。這是遞歸能夠停止的保證。

2. TreeNode* temp = ...;
   核心交換操作。我們先用一個臨時指針?temp?暫存左子節點的地址，然后將右子節點賦給左指針，最后將暫存的地址賦給右指針，完成了對當前節點?root?的直接子節點的交換。

3. invertTree(root->left); invertTree(root->right);
   分治與遞歸。這是“將軍下令”的步驟。我們對已經交換過來的新左子樹和新右子樹，分別進行遞歸調用。我們完全信任這兩個遞歸調用能完美地反轉它們各自內部的所有結構。

4. return root;
   返回結果。在完成了本層的交換和對子樹的遞歸反轉之后，當前?root?節點下的整棵子樹都已經完成了反轉。我們將這個?root?返回給它的上層調用。最終，最頂層的調用會返回整棵樹的新根節點（其實還是原來的那個根節點，但它的結構已經被改變了）。

---

四、總結與收獲

• 復雜度分析：我們恰好訪問了樹中的每一個節點一次來執行交換操作。因此，時間復雜度為?O(n)，其中 n 是節點的總數。遞歸調用棧的深度最壞情況下等于樹的高度，因此空間復雜度為?O(h)。

• 核心思想：對于樹這種具有天然遞歸結構的題目，分治思想是解決問題的金鑰匙。將一個大問題（反轉整棵樹）分解為三個小步驟：處理當前節點、遞歸處理左子樹、遞歸處理右子樹。

• 關鍵技巧：理解遞歸函數調用的本質。當你寫?invertTree(root->left)?時，你要在腦中形成一種“信任”——相信這個函數一定會返回一個已經完全反轉好的左子樹，而無需關心其內部細節。這種“定義與信任”是掌握遞歸的關鍵。