居然沒有題解？我來寫一下我的抽象做法。

---

題解

手玩一下，隨便畫個他信心的折線圖，如下：

可以發現，如果我們知道終止節點，那么我們就可以知道中間有多少個上升長度。（因為它只能 $+1$ 或者 $?1$）

然后可以發現一個性質，如果我們把連續的有出現的值在值域上看成一個聯通塊，如圖：

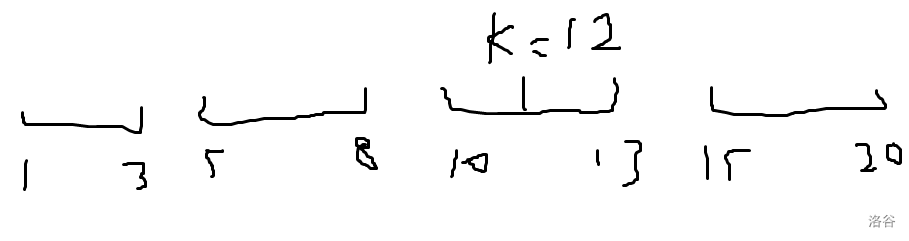
其中的線段表示這一段的值有出現過。顯然，$k$ 只能往左跳，不能跨過段往右跳。

那么可以考慮枚舉從右往左枚舉 $k$ 能否停在這個段內。

具體的，如圖：

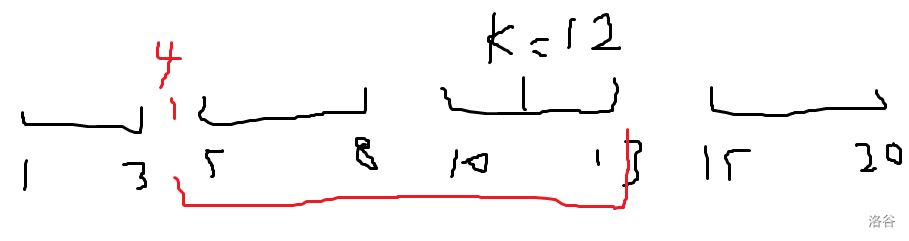
此時我們是在判斷區間 $[5,8]$ 是否合法，那么本質就是看 $k$ 能否停在區間 $[5,8]$ 前面一個區間右端點 $+1$ 往右的位置。

容易發現，紅色區間內的所有數又是有用的，可以作為 $+1$ 使用。

那么 $k$ 最終停在的位置就是 $k+c?(n?c)$

其中 $c$ 是紅色區間的可用 $+1$ 數量。

判斷結果是否比左邊界大，即可判定有沒有解。

另外有特殊情況，例如如圖，算出來 $k$ 最終的位置比 $8$ 大。

這意味著紅色區間內可用 $+1$ 比其它 $?1$ 多。

那么就需要這些 $+1$ 兩兩低消。而我們進入一個區間 $[l,r]$ 后，所能到達的右端點最大就是 $r+1$。

但是具體是不是 $r+1$ 呢？可以發現最終所停位置一定和 $n+k$ 的奇偶性相同，根據這個，對 $r$ 或者 $r+1$ 取一個 $\min$ 即可。

具體維護可以使用并查集。

當然還有一些小細節需要處理，具體地可以看代碼。

代碼

int n,k;
int c[N],cnt[N],fa[N],l[N],r[N],uur[N];
inline int ga(int x){return x==fa[x]?x:fa[x]=ga(fa[x]);
}
int vis[N];
void uni(int x,int y){int Fx=ga(x),Fy=ga(y);if(Fx==Fy)return ;fa[Fx]=Fy;l[Fy]=min(l[Fx],l[Fy]);r[Fy]=max(r[Fx],r[Fy]);c[Fy]+=c[Fx];
}
struct rrrr{int l,r,id;
}line[N];
void solve(){for(int i=1;i<N;i++)fa[i]=l[i]=r[i]=i,vis[i]=0,cnt[i]=0,c[i]=0,uur[i]=0;cin>>n>>k;for(int i=1;i<=n;i++){int x;cin>>x;cnt[x]++;c[x]++;}for(int i=1;i<=N-2;i++){if(cnt[i]&&cnt[i+1])uni(i,i+1);}int lid=0;for(int i=1;i<=N-2;i++){if(cnt[i]){int fi=ga(i);if(!vis[fi]){++lid;line[lid]={l[fi],r[fi],lid};uur[fi]=lid;vis[fi]=1;}}}for(int i=1;i<=N-2;i++)vis[i]=0;int id=0;int	resc=0;int ans=0;for(int i=k;i>=1;i--){if(cnt[i]){int fi=ga(i);if(vis[fi])continue;resc+=c[fi];//	cout<<fi<<":   \n";//	cout<<resc<<" ";int Lid=k+resc-(n-resc);//	cout<<Lid<<" ";if(Lid>line[uur[fi]-1].r){ans=min(Lid,((n+k)%2==(line[uur[fi]].r%2))?line[uur[fi]].r:line[uur[fi]].r+1);//	cout<<ans<<" ";cout<<(n-(k-ans))/2<<"\n";return ;}vis[fi]=1;}}cout<<resc<<"\n";
}