一、求二叉樹的值【層序遍歷實現】

序號	題目	鏈接
1	二叉樹的右視圖	https://leetcode.cn/problems/binary-tree-right-side-view/description/?envType=problem-list-v2&envId=tree
2	二叉樹的層最大值	https://leetcode.cn/problems/find-largest-value-in-each-tree-row/description/?envType=problem-list-v2&envId=tree
3	二叉樹的第K大的層和	https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/description/?envType=problem-list-v2&envId=tree
4	層數最深的葉子節點的和	https://leetcode.cn/problems/deepest-leaves-sum/description/?envType=problem-list-v2&envId=tree
5	二叉樹的層平均值	https://leetcode.cn/problems/average-of-levels-in-binary-tree/description/?envType=problem-list-v2&envId=tree
6	最大層和的層號	https://leetcode.cn/problems/maximum-level-sum-of-a-binary-tree/description/?envType=problem-list-v2&envId=tree

1.1右視圖

vector<int> rightSideView(TreeNode* root) {vector<int> result;if(root==nullptr) return result;queue<TreeNode*> Q;Q.push(root);int num=0;//層序遍歷的最后一個值while(!Q.empty()){int n=Q.size();while(n--){TreeNode* p=Q.front();Q.pop();num=p->val;if(p->left!=nullptr) Q.push(p->left);if(p->right!=nullptr) Q.push(p->right);}result.push_back(num);}return result;
}

1.2層最大值

vector<int> largestValues(TreeNode* root) {if(root==nullptr) return {};vector<int> result;//用來存放每一層的最大值queue<TreeNode*> Q;Q.push(root);while (!Q.empty()) {int n=Q.size(); // 當前層的節點數量int maxval=INT_MIN;//用來存放當前層的最大值for (int i=0; i<n; i++) {TreeNode* node = Q.front();Q.pop();maxval=max(maxval,node->val);//求最大值if (node->left != nullptr)  Q.push(node->left);if (node->right != nullptr) Q.push(node->right);}result.push_back(maxval);//將當前層的最大值加入集合中}return result;
}

1.3層和

long long kthLargestLevelSum(TreeNode* root, int k) {queue<TreeNode*> Q;Q.push(root);vector<long long> s;while(!Q.empty()){int n=Q.size();//每一層的節點數long long sum=0;//每一層的總和for(int i=0;i<n;i++){TreeNode* node=Q.front();Q.pop();sum+=node->val;//求層和if(node->left!=nullptr) Q.push(node->left);if(node->right!=nullptr) Q.push(node->right);}s.push_back(sum);//將每一層的層和放入數組中}//排序，返回第K大的if(s.size() < k) return -1;sort(s.begin(), s.end());return s[s.size()-k];
}

1.4最底層的葉子結點的和

int deepestLeavesSum(TreeNode* root) {vector<double> result;queue<TreeNode*> Q;Q.push(root);int sum=0;//層和while(!Q.empty()){int n=Q.size();//每一層的節點個數sum=0;//每一層初始為0while(n--){TreeNode* p=Q.front();Q.pop();sum +=p->val;if(p->left!=nullptr) Q.push(p->left);if(p->right!=nullptr) Q.push(p->right);}}return sum;//sum會被覆蓋成最后一層的層和
}

1.5層平均值

vector<double> averageOfLevels(TreeNode* root) {vector<double> result;queue<TreeNode*> Q;Q.push(root);while(!Q.empty()){int n=Q.size();//每一層的節點數double sum=0;//求平均數for(int i=0;i<n;i++){TreeNode* p=Q.front();Q.pop();sum+=p->val;//求層和if(p->left!=nullptr) Q.push(p->left);if(p->right!=nullptr) Q.push(p->right);}sum=sum/n;//每一層結束之后，計算平均值，并加入結果result.push_back(sum);}return result;
}

1.6最大層和的層號

int maxLevelSum(TreeNode* root) {queue<TreeNode*> Q;Q.push(root);int maxSum = INT_MIN;  // 記錄最大層和int maxLevel = 1;      // 記錄最大層和對應的層號（默認為第一層）int currentLevel = 0;  // 當前層數（根節點為第一層）while(!Q.empty()){currentLevel++;int n=Q.size();//每一層的節點數long long sum=0;//每一層的總和for(int i=0;i<n;i++){TreeNode* node=Q.front();Q.pop();sum+=node->val;//求層和if(node->left!=nullptr) Q.push(node->left);if(node->right!=nullptr) Q.push(node->right);}// 更新最大層和及對應的層號if (sum > maxSum) {maxSum = sum;maxLevel = currentLevel;}}return maxLevel;
}

二、二叉樹的路徑

序號	題目	鏈接
1	根節點到葉子結點，二叉樹的所有路徑	https://leetcode.cn/problems/binary-tree-paths/description/?envType=problem-list-v2&envId=tree
2	根節點到葉子結點，是否存在和為target的路徑	https://leetcode.cn/problems/path-sum/description/?envType=problem-list-v2&envId=tree
3	根節點到葉子結點，和為target的路徑	https://leetcode.cn/problems/path-sum-iii/description/?envType=problem-list-v2&envId=tree
1	路徑的十進制之和	https://leetcode.cn/problems/sum-root-to-leaf-numbers/description/?envType=problem-list-v2&envId=tree
2	路徑的二進制之和	https://leetcode.cn/problems/sum-of-root-to-leaf-binary-numbers/description/?envType=problem-list-v2&envId=tree
1	二叉樹里，路徑之和為target的路徑	https://leetcode.cn/problems/path-sum-ii/description/?envType=problem-list-v2&envId=tree

2.1根節點到葉子節點，二叉樹的路徑

返回所有從根節點到葉子節點的路徑。

用 先序遍歷（先處理當前節點，再遞歸子節點），因為需要先記錄當前節點值，再延伸到子節點。

• 遞歸終止條件1：空節點直接返回
• 遞歸終止條件2：訪問到葉節點，路徑完整，加入結果集

void dfs(TreeNode* root,string path, vector<string>& result){if(root==nullptr) return ;path=path+to_string(root->val);//訪問到葉子節點結束if(root->left==nullptr && root->right==nullptr){result.push_back(path);return ;}//左右dfs(root->left,path+"->",result);dfs(root->right,path+"->",result);
}
vector<string> binaryTreePaths(TreeNode* root) {if(root==nullptr) return {};vector<string> res;dfs(root,"",res);return res;
}

給你二叉樹的根節點 root 和一個表示目標和的整數 targetSum 。判斷該樹中是否存在 根節點到葉子節點 的路徑，這條路徑上所有節點值相加等于目標和 targetSum 。如果存在，返回 true ；否則，返回 false 。

將每條路徑的和加起來=path，將多條path存儲起來放入result中。
判斷result中是否存在一條路徑的和=target。

void dfs(TreeNode* root, int path, vector<int>& result){if(root==nullptr) return ;path+=root->val;if(root->left==nullptr && root->right==nullptr){result.push_back(path);return ;}dfs(root->left, path, result);dfs(root->right, path, result);
}
bool hasPathSum(TreeNode* root, int targetSum) {vector<int> res;dfs(root,0,res);//遍歷所有路徑的和，若有一條=target則返回1for(int r:res){if(r==targetSum) return 1;}return 0;
}

給你二叉樹的根節點 root 和一個整數目標和 targetSum ，找出所有 從根節點到葉子節點 路徑總和等于給定目標和的路徑。

存儲路徑（path），路徑集合（result）。在路徑集合中，遍歷每條路徑，相加，與target比較。

void dfs(TreeNode* root, vector<int> path, vector<vector<int>>& result){if(root==nullptr) return ;path.push_back(root->val);//存儲路徑if(root->left==nullptr && root->right==nullptr){result.push_back(path);return ;}dfs(root->left, path, result);dfs(root->right, path, result);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {vector<vector<int>> res;//所有路徑結果vector<vector<int>> h;//正確路徑結果dfs(root,{},res);//遍歷每條路徑，將路徑集合的節點相加，與target比較for(vector<int> r:res){int sum=0;for(int num:r){sum+=num;}if(sum==targetSum) h.push_back(r);}return h;
}

2.2路徑的十進制之和 & 二進制之和

給你一個二叉樹的根節點 root ，樹中每個節點都存放有一個 0 到 9 之間的數字。
每條從根節點到葉節點的路徑都代表一個數字：
例如，從根節點到葉節點的路徑 1 -> 2 -> 3 表示數字 123 。

void dfs(TreeNode *root, int path, int& result) {if (root == nullptr) return ;path = path*10+root->val;if (root->left == nullptr && root->right == nullptr) {result+=path;return ;}dfs(root->left,path,result);dfs(root->right,path,result);}
int sumNumbers(TreeNode* root) {int totalSum = 0;dfs(root, 0, totalSum);return totalSum;
}

給出一棵二叉樹，其上每個結點的值都是 0 或 1 。每一條從根到葉的路徑都代表一個從最高有效位開始的二進制數。
例如，如果路徑為 0 -> 1 -> 1 -> 0 -> 1，那么它表示二進制數 01101，也就是 13 。
對樹上的每一片葉子，我們都要找出從根到該葉子的路徑所表示的數字。

只需要將上述每條路徑的計算方式修改即可。

path = (path << 1) | root->val;
path = path*2+root->val;

2.3二叉樹里的路徑

給定一個二叉樹的根節點 root ，和一個整數 targetSum ，求該二叉樹里節點值之和等于 targetSum 的 路徑 的數目。
路徑 不需要從根節點開始，也不需要在葉子節點結束，但是路徑方向必須是向下的（只能從父節點到子節點）。

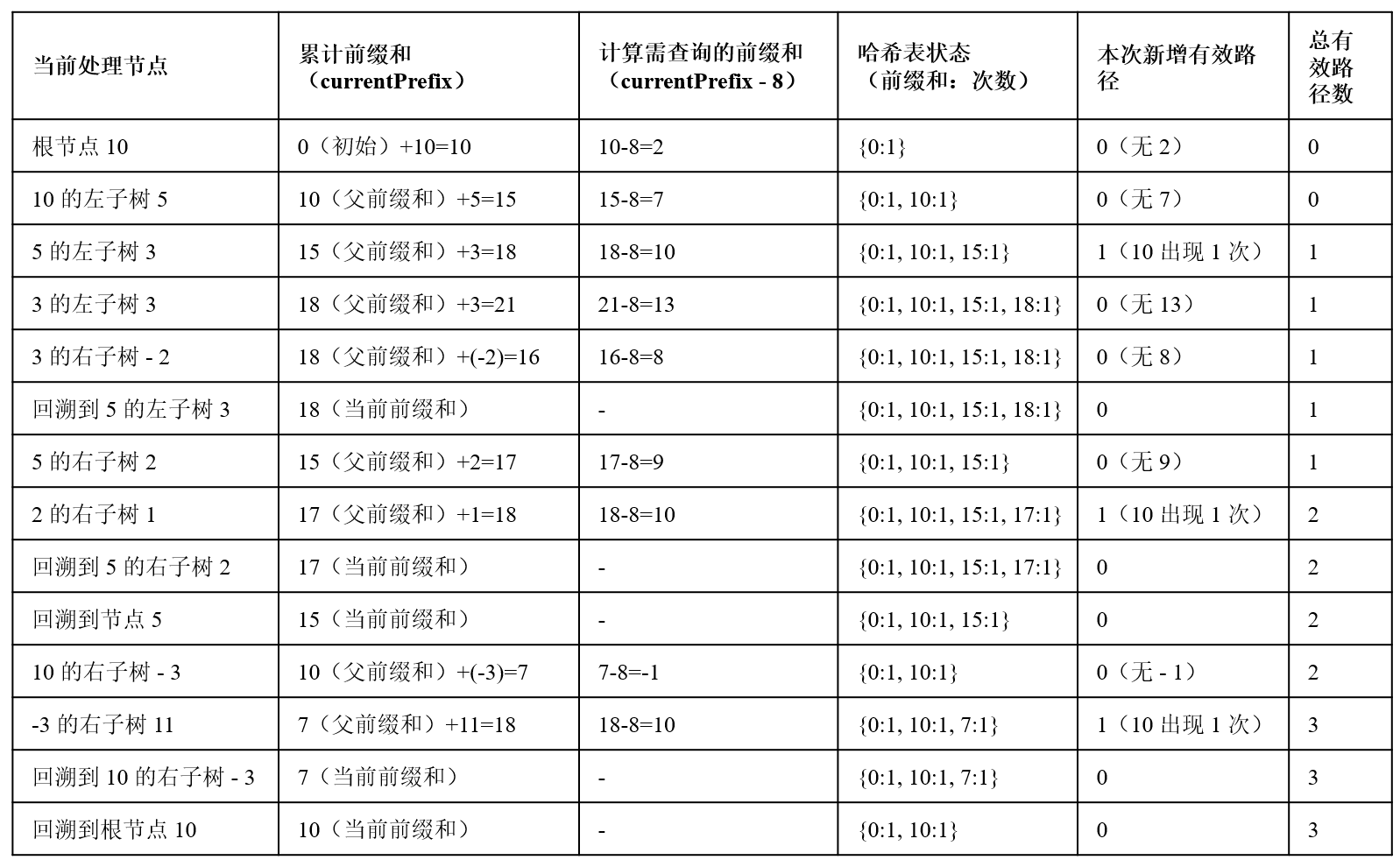
• 前綴和定義：從根節點到當前節點的路徑上，所有節點值的累加和，記為 prefixSum。
• 路徑和與前綴和的關系：若從節點 A 到節點 B 的路徑和為 targetSum，則 prefixSum(B) - prefixSum(A的父節點) = targetSum（即 prefixSum(A的父節點) = prefixSum(B) - targetSum）。
  = 哈希表作用：記錄 “前綴和出現的次數”，遍歷到當前節點時，直接查詢 prefixSum - targetSum 出現的次數，即為以當前節點為終點的有效路徑數。

int dfs(TreeNode* node, long long currentPrefix, int target, unordered_map<long long, int>& prefixCount) {if (node == nullptr) return 0;currentPrefix += node->val;// 計算當前有效路徑數int res = prefixCount[currentPrefix - target];// 更新前綴和計數prefixCount[currentPrefix]++;// 遞歸左右子樹res += dfs(node->left, currentPrefix, target, prefixCount);res += dfs(node->right, currentPrefix, target, prefixCount);// 回溯prefixCount[currentPrefix]--;return res;
}
int pathSum(TreeNode* root, int targetSum) {unordered_map<long long, int> prefixCount;prefixCount[0] = 1; // 初始化前綴和為0的情況return dfs(root, 0, targetSum, prefixCount);
}

// 內層遞歸：計算從start節點開始，向下所有路徑中和為target的數目
int countPathFromRoot(TreeNode* start, long long target) {if (start == nullptr) return 0;// 當前節點值等于target，說明存在1條路徑（僅當前節點）int count = (start->val == target) ? 1 : 0;// 遞歸延伸到左子樹和右子樹，target減去當前節點值（剩余需要的和）count += countPathFromRoot(start->left, target - start->val);count += countPathFromRoot(start->right, target - start->val);return count;
}
int pathSum(TreeNode* root, int targetSum) {if (root == nullptr) return 0;// 1. 計算以當前節點為起點的路徑中，和為targetSum的數目int count = countPathFromRoot(root, targetSum);// 2. 遞歸處理左子樹和右子樹，找其他起點count += pathSum(root->left, targetSum);count += pathSum(root->right, targetSum);return count;
}

三、二叉樹的路徑2

序號	題目	鏈接
1	最長同值路徑	https://leetcode.cn/problems/longest-univalue-path/description/?envType=problem-list-v2&envId=tree
2	左葉子之和	https://leetcode.cn/problems/sum-of-left-leaves/description/?envType=problem-list-v2&envId=tree
3	好節點的個數	https://leetcode.cn/problems/count-good-nodes-in-binary-tree/description/?envType=problem-list-v2&envId=tree
4	好節點對的數量	https://leetcode.cn/problems/number-of-good-leaf-nodes-pairs/description/?envType=problem-list-v2&envId=tree
5	路徑和相等的最小代價	https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/description/?envType=problem-list-v2&envId=tree
6	最長交錯路徑	https://leetcode.cn/problems/longest-zigzag-path-in-a-binary-tree/description/?envType=problem-list-v2&envId=tree
7	二叉樹的最大路徑和	https://leetcode.cn/problems/binary-tree-maximum-path-sum/description/?envType=study-plan-v2&envId=top-100-liked

3.1最長同值路徑

給定一個二叉樹的 root ，返回 最長的路徑的長度 ，這個路徑中的 每個節點具有相同值 。 這條路徑可以經過也可以不經過根節點。
兩個節點之間的路徑長度 由它們之間的邊數表示。

用后序遍歷，葉子節點是基礎（延伸長度 0），向上每層節點基于子節點結果 “加 1”（如果值相同），最終根節點匯總全局最長路徑。

int maxlength = 0;
int dfs(TreeNode* root){if(root==nullptr) return 0;int leftlength=dfs(root->left);int rightlength=dfs(root->right);//左子樹節點if(root->left!=nullptr && root->left->val == root->val) leftlength++;else leftlength=0;//右子樹節點if(root->right!=nullptr && root->right->val == root->val) rightlength++;else rightlength=0;//更新全局最長路徑長度maxlength=max(maxlength, leftlength+rightlength);//返回從當前節點出發的最長同值路徑return max(leftlength, rightlength);
}
int longestUnivaluePath(TreeNode* root) {if (root == nullptr) return 0;dfs(root);return maxlength;
}

3.2左葉子之和

給定二叉樹的根節點 root ，返回所有左葉子之和。

int num=0;
//用棧實現先序遍歷
void f(TreeNode* root){if(root==nullptr) return ;stack<TreeNode*> st;st.push(root);while(!st.empty()){TreeNode* p=st.top();st.pop();//result.push_back(p->val);if(p->right!=nullptr) st.push(p->right);//if(p->left!=nullptr) st.push(p->left);if(p->left!=nullptr){if(p->left->left==nullptr && p->left->right==nullptr) num+=p->left->val;else st.push(p->left);}  }
}
int sumOfLeftLeaves(TreeNode* root) {f(root);return num;
}

void dfs(TreeNode* node, int& sum) {if (node == nullptr) return;// 檢查當前節點的左子節點是否為左葉子if (node->left != nullptr) {// 左子節點是葉子節點，累加左葉子的值if (node->left->left == nullptr && node->left->right == nullptr) {sum += node->left->val; }// 不是葉子節點，繼續遞歸左子樹else  dfs(node->left, sum);}// 遞歸處理右子樹dfs(node->right, sum);
}
int sumOfLeftLeaves(TreeNode* root) {if(root==nullptr) return 0;int sum=0;dfs(root,sum);ret

3.3好節點 & 好節點對

給你一棵根為 root 的二叉樹，請你返回二叉樹中好節點的數目。
好節點的 定義為：從根到該節點 X 所經過的節點中，沒有任何節點的值大于 X 的值。

int goodNodes(TreeNode* root) {return dfs(root, root->val);
}
//maxval是從根到node的路徑最大值
int dfs(TreeNode* node,int maxval){if(node==nullptr) return 0;int count=0;if(node->val >= maxval){count=1;maxval=node->val;}count += dfs(node->left, maxval);count += dfs(node->right,maxval);return count;
}

給你二叉樹的根節點 root 和一個整數 distance 。
如果二叉樹中兩個 葉 節點之間的 最短路徑長度 小于或者等于 distance ，那它們就可以構成一組 好葉子節點對 。

vector<int> dfs(TreeNode* root, int distance, int& ans) {if (root == nullptr) return {};if (root->left == nullptr && root->right == nullptr) return { 0 };vector<int> ret;auto left = dfs(root->left, distance, ans);for (auto& e : left) {if (++e > distance) continue;ret.push_back(e);}auto right = dfs(root->right, distance, ans);for (auto& e : right) {if (++e > distance) continue;ret.push_back(e);}for (auto l : left) {for (auto r : right) {ans += (l + r <= distance);}}return ret;
}
int countPairs(TreeNode* root, int distance) {int ans = 0;dfs(root, distance, ans);return ans;
}

3.4路徑和相等的最小代價

int minIncrements(int n, vector<int>& cost) {int res = 0;  // 記錄總增加量// 從最后一個非葉子節點開始向上遍歷（非葉子節點范圍：1 ~ (n-1)/2）for (int i = (n - 1) / 2; i >= 1; --i) {// 左孩子索引 = 2*i - 1（節點i的左孩子是2i，對應cost索引=2i-1）// 右孩子索引 = 2*i（節點i的右孩子是2i+1，對應cost索引=2i）int left = cost[2 * i - 1];  int right = cost[2 * i];// 左右子樹路徑和的差值就是需要增加的量（讓兩者相等）res += abs(left - right);// 更新當前節點的累計值：取左右子樹的最大值 + 當前節點原值// （這個值會傳遞給上層節點，作為當前子樹的總路徑和）cost[i - 1] += max(left, right);}return res;
}

3.5最長交錯路徑

給你一棵以 root 為根的二叉樹，二叉樹中的交錯路徑定義如下：

• 選擇二叉樹中 任意 節點和一個方向（左或者右）。如果前進方向為右，那么移動到當前節點的的右子節點，否則移動到它的左子節點。
• 改變前進方向：左變右或者右變左。重復第二步和第三步，直到你在樹中無法繼續移動。
• 交錯路徑的長度定義為：訪問過的節點數目 - 1（單個節點的路徑長度為 0 ）。

// 后序遍歷：返回一個數組，[0]是當前節點的左啟路徑長度，[1]是右啟路徑長度
vector<int> postorder(TreeNode* node, int& max_len) {// 空節點的左啟、右啟路徑長度均為-1（方便父節點計算時+1后得到0，對應無孩子的情況）if (node == nullptr) return {-1, -1};// 1. 遞歸計算左、右子節點的路徑長度vector<int> left_info = postorder(node->left, max_len);   // left_info[0]：左子的左啟，[1]：左子的右啟vector<int> right_info = postorder(node->right, max_len); // right_info[0]：右子的左啟，[1]：右子的右啟// 2. 計算當前節點的左啟、右啟路徑長度int curr_left = 0;  // 當前節點的左啟路徑長度int curr_right = 0; // 當前節點的右啟路徑長度// 若有左子節點：當前左啟長度 = 左子的右啟長度 + 1（向左后需切換為右）if (node->left != nullptr)  curr_left = left_info[1] + 1;// 若有右子節點：當前右啟長度 = 右子的左啟長度 + 1（向右后需切換為左）if (node->right != nullptr)  curr_right = right_info[0] + 1;// 3. 更新全局最長路徑長度（當前節點的左啟、右啟路徑長度取最大值）max_len = max(max_len, max(curr_left, curr_right));// 4. 返回當前節點的路徑信息，供父節點使用return {curr_left, curr_right};
}
int longestZigZag(TreeNode* root) {int max_len = 0;  // 全局最長交錯路徑長度postorder(root, max_len);return max_len;
}

3.6二叉樹中的最大路徑和

二叉樹中的 路徑 被定義為一條節點序列，序列中每對相鄰節點之間都存在一條邊。同一個節點在一條路徑序列中 至多出現一次 。該路徑 至少包含一個 節點，且不一定經過根節點。

// 后序遍歷：返回當前節點的“最大單邊路徑和”（供父節點使用）
int dfs(TreeNode* node, int& maxsum) {if (node == nullptr)  return 0; // 1. 遞歸計算左、右子節點的單邊路徑和（過濾負的子路徑和，取0表示“不選該子樹”）int left = max(dfs(node->left, maxsum), 0);int right = max(dfs(node->right, maxsum), 0);// 2. 計算當前節點的“最大完整路徑和”，并更新全局最大和int curr = node->val + left + right;maxsum = max(maxsum, curr);// 3. 返回當前節點的“最大單邊路徑和”（供父節點組合）return node->val + max(left, right);
}
int maxPathSum(TreeNode* root) {int maxsum = INT_MIN;  // 全局最大路徑和（初始為最小整數，避免節點值全為負的情況）dfs(root, maxsum);return maxsum;
}