數模的完備性一直是國賽中評審的重點，也是大家賽中最容易失分的點。具體來講，2023年C題國一使用了ARIMA,很多省三論文也是ARIMA。二者之所以出現這種巨大的等級差異不是因為模型問題，而是后者模型并不完備，缺少很多模型必要元素。

針對國賽數學模型的完備性 創新性錄制了四個視頻作為課程模型篇的序言課，希望能夠對大家賽中有所幫助。

在數學建模中，模型假設是連接實際問題與數學模型的橋梁。恰當的假設能夠簡化問題、突出核心矛盾，使模型既具備可操作性，又盡量貼近現實。通常模型假設可分為以下幾類：

1. 前提假設（基本設定類）

前提假設用于明確研究問題的基本框架，是模型建立的起點。

研究對象：界定問題所針對的主體，例如某個市場、某類人群或某一物理系統。

研究范圍：限定分析的空間與時間范圍，避免無限擴展。

環境穩定性：假設外部環境在研究期間保持基本不變，為模型提供穩定背景。

2. 簡化假設（理想化處理類）

現實問題往往復雜難解，必須通過合理的簡化來保證模型的可解性。

忽略次要因素：將對結果影響較小的因素排除在外。

理想化處理：對復雜過程進行抽象，例如假設市場完全競爭、忽略摩擦力等。

3. 參數假設（數值設定類）

很多情況下，部分參數或常數難以直接獲得，需要人為設定。

參數取值方式：通過經驗數據、文獻參考或合理推斷確定數值。

常數設定：對研究中需要固定的量（如利率、溫度）進行假定。

4. 變量關系假設（結構性假設）

模型的核心在于變量之間的關系，而關系本身也需要假設支撐。

線性/非線性關系：變量間是否存在線性相關性。

因果作用：明確哪些變量是自變量，哪些是因變量。

交互效應：假設變量之間是否存在聯動或耦合效應。

5. 動態/靜態假設（時間性假設）

時間維度的處理方式決定了模型的適用場景。

靜態假設：研究對象在某一時刻或較短周期內的特征，不考慮時間演化。

動態假設：考慮系統隨時間變化的過程，刻畫長期趨勢或演化規律。

6. 確定性/隨機性假設

對輸入與結果的確定性進行說明。

確定性模型：所有輸入參數與系統結果固定不變，重復實驗條件下結果一致。

隨機性模型：引入隨機變量，假設其服從特定概率分布，更貼近現實中的不確定性。

7. 邊界條件與環境假設

邊界與環境是系統運行的重要前提。

邊界固定：如管道流體不泄漏、區域范圍不變。

環境恒定：假設溫度、市場條件或政策環境保持穩定。

系統開放/封閉：說明模型是否考慮外部輸入或輸出。

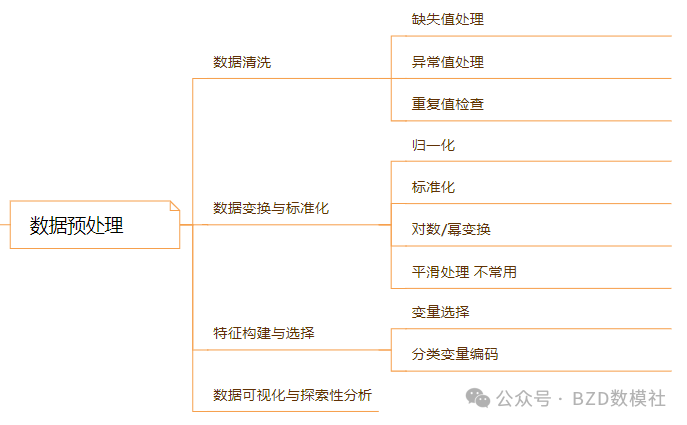
數據預處理

在數學建模與數據分析過程中，數據預處理是保證模型有效性和可靠性的關鍵步驟。原始數據往往存在噪聲、缺失和不一致性，如果不加以處理，會嚴重影響模型的穩定性與結果的可信度。常見的數據預處理工作包括以下幾個方面：

1. 數據清洗

數據清洗旨在提高數據的質量和完整性，使其能夠更好地支持后續建模。

缺失值處理：對缺失數據進行合理填補，例如刪除缺失比例過大的樣本，或采用均值、插值、回歸等方法進行估算。

異常值處理：識別并剔除不合理的極端值，或通過箱型圖、Z-Score 等方法進行判斷，必要時可用合理值替代。

重復值檢查：檢查并刪除重復記錄，避免樣本權重被無意放大。

2. 數據變換與標準化

為了保證模型的穩定性和變量間的可比性，需要對數據進行數值變換。

歸一化：將不同量綱的數據縮放到統一區間（如 [0,1]），適用于神經網絡等對數值范圍敏感的模型。

標準化：將變量轉換為均值為 0、方差為 1 的分布，消除不同變量尺度差異的影響。

對數/冪變換：在數據分布偏態或存在較大波動時，對變量進行對數或冪次變換，使其更符合正態分布假設。

平滑處理（較少使用）：通過移動平均、加權平均等方式，削弱數據中的隨機波動。

3. 特征構建與選擇

合理的特征工程能顯著提升模型的解釋力與預測性能。

變量選擇：篩選與目標變量高度相關的特征，剔除冗余或無關變量，以減少維度災難。

分類變量編碼：將定性變量轉換為數值型變量，例如獨熱編碼（One-hot Encoding）或序數編碼（Ordinal Encoding），以便模型能夠識別與利用。

4. 數據可視化與探索性分析

在正式建模前，應通過數據可視化與探索性分析（Exploratory Data Analysis, EDA）對數據分布、變量關系進行初步理解。

使用直方圖、散點圖、箱線圖等方法，直觀展示變量的分布特征與相互關系。

結合相關系數或熱力圖，分析變量之間的線性或非線性相關性。

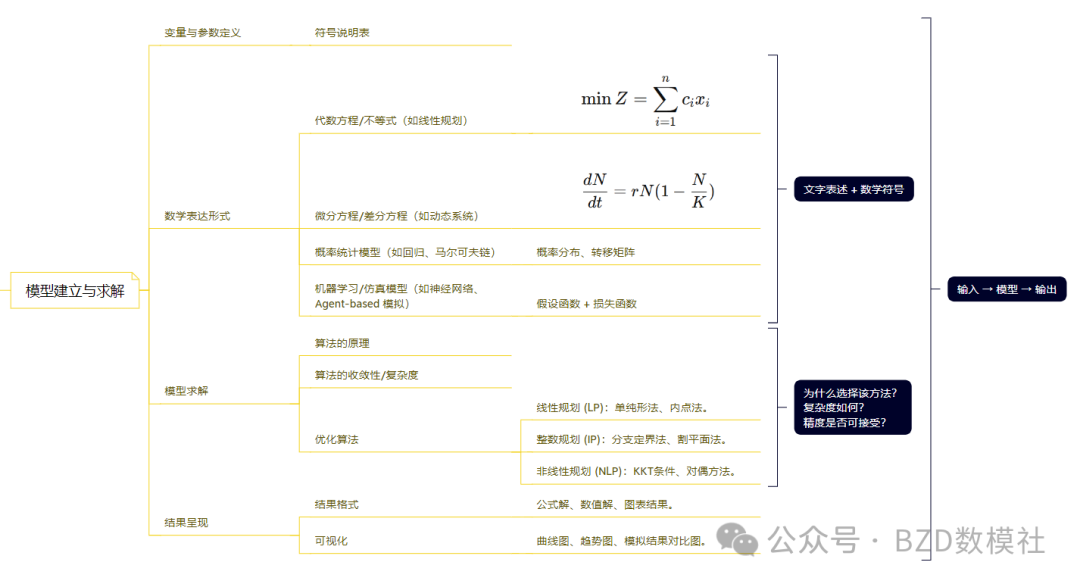
模型建立與求解

模型建立與求解是數學建模論文的核心環節，其任務是將問題的實際情境轉化為數學結構，并通過合理的求解方法獲得可解釋的結果。完整的過程包括變量與參數的定義、數學形式的表達、模型的求解以及結果的呈現。

1. 變量與參數定義

在模型構建之前，必須對問題中的各類量進行嚴格定義。

符號說明表：統一說明自變量、因變量、參數和常數的符號含義及單位，保證模型的可讀性與規范性。

明確角色區分：區分可控變量、狀態變量與外部干擾量，為后續方程構建提供清晰框架。

2. 數學表達形式

不同類型的問題需要采用不同的數學工具加以描述。常見形式包括：

代數方程與不等式：用于表示線性或非線性規劃問題，如資源分配、路徑優化等。

微分方程與差分方程：適用于動態系統或時間演化過程，能夠刻畫系統狀態隨時間的變化規律。

概率統計模型：如回歸模型、馬爾可夫鏈等，能夠刻畫不確定性過程，包括概率分布設定和轉移矩陣構建。

機器學習與仿真模型：如神經網絡、支持向量機、Agent-based 模擬等，通常以假設函數與損失函數為核心，強調預測能力與復雜系統仿真。

結果分析

1. 合理性檢驗

首先，需要檢驗模型解是否符合基本的現實常識與邏輯。例如，預測的人口規模應為正數且隨時間變化趨勢合理，規劃模型的資源分配結果不能超過總供給。通過與直覺和常理的對照，可以初步判斷模型結果是否可信。

2. 數據驗證

數據驗證是衡量模型有效性的重要手段。具體做法是將模型結果與實驗數據或歷史數據進行對比，檢驗其精度與適用性。如果模型預測與真實數據高度吻合，則說明其可靠性較高；若差異較大，則需要反思假設合理性或模型結構是否需要調整。

3. 敏感性分析

為了進一步檢驗模型的穩健性，需要研究不同參數取值對結果的影響。通過對關鍵參數進行擾動并觀察結果變化，可以揭示模型對輸入的敏感程度。例如，若輕微的參數變化導致結果劇烈波動，說明模型存在不穩定性；反之，結果變化平緩則表明模型具有較好的穩健性。

4. 魯棒性檢驗（可選）

在部分研究中，還需考察模型在不同環境或場景下的適用性，即魯棒性。例如，預測模型在不同數據集、不同初始條件下是否仍能保持較高的精度。這一分析雖在常規賽題中使用較少，但若能體現，將顯著增強模型的學術價值與推廣價值。