【機器學習入門】5.2 回歸的起源——從身高遺傳到線性模型的百年演變

提到 “回歸”，很多剛入門的同學會覺得它是個抽象的數學概念，但你可能想不到，這個術語的誕生，竟然源于 19 世紀一位生物學家對 “身高遺傳” 的研究。回歸分析從 “觀察生物現象” 出發，逐步發展成機器學習中預測連續值的核心工具，這背后藏著一段有趣的科學史。

這篇文章會沿著 “歷史脈絡” 展開，從 “回歸的提出者（高爾頓）” 講起，詳細拆解他的身高遺傳實驗、“向均值回歸” 現象的發現、“回歸” 術語的由來，再到線性回歸模型的雛形，讓你不僅懂 “回歸是什么”，更懂 “它從哪里來”，全程貼合入門認知，不堆砌復雜公式，用生活化的例子還原這段科學歷程。

一、回歸的 “創始人”：弗朗西斯?高爾頓（Sir Francis Galton）

要講回歸的起源，必須先認識一個人 ——弗朗西斯?高爾頓（1822-1911），英國著名的生物學家、統計學家，也是 “進化論之父” 達爾文的表弟。

高爾頓的研究興趣非常廣泛，從氣象學到遺傳學，但讓他與 “回歸” 結緣的，是他對 “遺傳規律” 的探索 ——19 世紀末，他一直困惑一個問題：
“如果父母身高很高，他們的孩子會不會越來越高？如果父母身高很矮，孩子會不會越來越矮？長此以往，人類的身高會不會出現‘極端分化’（要么特別高，要么特別矮）？”

為了回答這個問題，他做了一項劃時代的研究，這也成為 “回歸分析” 的起點。

二、關鍵實驗：身高遺傳的 “向均值回歸” 現象

高爾頓沒有停留在猜想，而是通過 “數據收集 + 分析” 驗證自己的疑問，整個實驗過程清晰且嚴謹，即使放在今天看，也符合科學研究的邏輯。

2.1 實驗第一步：收集數據 —— 幾百個家庭的身高記錄

高爾頓聯合助手，收集了近 1000 個家庭的身高數據，涵蓋父母和子女（每個家庭至少包含 1 位父母和 1 位成年子女）。為了簡化分析，他做了兩個關鍵處理：

統一 “父母身高” 計算方式：將 “父親身高” 和 “母親身高 ×1.08”（當時認為母親身高需換算成 “等效父親身高”，避免性別差異影響）取平均值，得到 “父母平均身高”（記為x）；
聚焦 “成年子女身高”：只統計子女成年后的身高（記為y），避免年齡對身高的影響。

最終，他得到了一組 “父母平均身高 - 子女身高” 的配對數據，比如（父母平均 72 英寸，子女 70 英寸）、（父母平均 62 英寸，子女 64 英寸）等（注：1 英寸≈2.54 厘米，當時英國常用英寸作為身高單位）。

2.2 實驗第二步：分析數據 —— 意外發現 “向均值回歸”

高爾頓將收集到的數據繪制成 “散點圖”（橫軸是父母平均身高x，縱軸是子女身高y），然后觀察數據的分布規律，結果卻出乎他的意料：
身高并沒有出現 “極端分化”，反而呈現 “向均值靠攏” 的趨勢—— 這就是后來被稱為 “向均值回歸（Regression to the Mean）” 的核心現象。

我們用具體數據舉例，更直觀理解這個現象（當時英國成年男性的平均身高約為 68 英寸）：

高個子父母組：父母平均身高 72 英寸（比均值高 4 英寸），他們的子女平均身高約為 70 英寸（比均值高 2 英寸）—— 子女比父母矮，向均值靠攏；
矮個子父母組：父母平均身高 62 英寸（比均值低 6 英寸），他們的子女平均身高約為 64 英寸（比均值低 4 英寸）—— 子女比父母高，也向均值靠攏；
中等身高父母組：父母平均身高 68 英寸（等于均值），他們的子女平均身高也接近 68 英寸 —— 基本穩定在均值附近。

高爾頓在論文中描述這個現象時說：“身高的遺傳就像被一根‘無形的線’拉著，極端值總會向平均水平回歸，這讓人類身高在長期中保持穩定，不會出現極端分化。”

2.3 “回歸” 術語的誕生：從 “Regression” 到中文翻譯

高爾頓在 1886 年發表的《遺傳的身高向均值回歸》論文中，第一次使用 “Regression” 這個詞來描述上述現象 ——“Regression” 在拉丁語中本意是 “回到之前的狀態”，在這里特指 “子女身高回到人類平均身高的狀態”。

后來，這個術語被統計學家沿用，并逐步推廣到更廣泛的領域：只要數據呈現 “極端值向均值靠攏” 的規律，都可以稱為 “回歸現象”；而用于分析這種現象的數學方法，就被稱為 “回歸分析”。

到了 20 世紀，回歸分析傳入中國，“Regression” 被翻譯成 “回歸”，既保留了 “回到均值” 的核心含義，又簡潔易懂，一直沿用至今。

三、從 “現象” 到 “模型”：線性回歸的雛形

高爾頓沒有止步于發現 “向均值回歸” 現象，他進一步思考：“父母身高和子女身高之間，是否存在可量化的數學關系？能不能用一個公式，根據父母身高預測子女身高？”

這一步，他從 “生物學家” 變成了 “統計學家”，也為后來的 “線性回歸模型” 奠定了基礎。

3.1 擬合 “線性預測線”：找到身高遺傳的數學規律

高爾頓將 “父母平均身高x” 和 “子女身高y” 的散點圖放在坐標系中，發現這些點雖然分散，但整體呈現 “線性趨勢”—— 可以用一條直線來近似描述兩者的關系。

他通過當時的 “最小二乘法”（一種讓直線與散點 “距離最近” 的數學方法），擬合出了第一條 “身高遺傳預測線”，對應的公式（以英寸為單位）為：y=33.73+0.516x

我們來拆解這個公式的含義（入門階段不用糾結計算細節，重點看物理意義）：

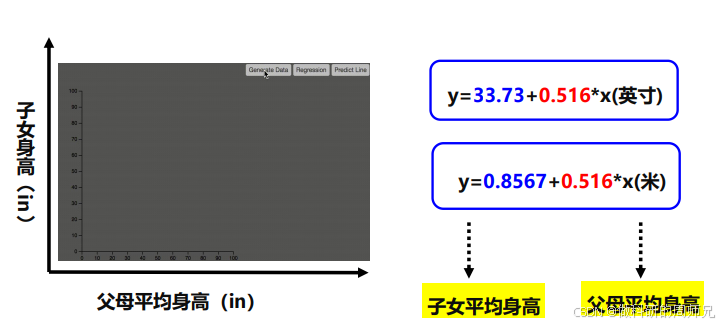
x：父母平均身高（單位：英寸）；
y：預測的子女身高（單位：英寸）；
斜率 0.516：表示 “父母身高每增加 1 英寸，子女身高平均增加 0.516 英寸”—— 這體現了遺傳的 “傳遞強度”，小于 1 說明子女身高不會像父母那樣極端，符合 “向均值回歸” 規律；
截距 33.73：表示 “當父母平均身高為 0 英寸（極端情況）時，子女身高的基礎值”—— 主要用于調整公式的整體水平，讓預測更貼合實際數據。

例子：用公式預測子女身高

假設一對父母的平均身高是 72 英寸（高個子父母），代入公式：y=33.73+0.516×72=33.73+37.152=70.882英寸
約等于 71 英寸，比父母平均身高 72 英寸矮，符合 “向均值回歸”（均值 68 英寸）的規律，和高爾頓觀察到的現象完全一致。

3.2 單位換算：從英寸到米的適配

隨著國際單位制的推廣，身高單位逐漸從 “英寸” 改為 “米”，高爾頓的公式也被調整為米的版本（保持數學關系不變）：y=0.8567+0.516x

其中：

x：父母平均身高（單位：米）；
y：預測的子女身高（單位：米）；
斜率仍為 0.516：說明 “遺傳傳遞強度” 與單位無關，是身高遺傳的固有規律；
截距 0.8567：對應英寸公式的 33.73 英寸（33.73×2.54≈85.67 厘米 = 0.8567 米）。

例子：米單位下的預測

父母平均身高 1.83 米（約 72 英寸），代入公式：y=0.8567+0.516×1.83≈0.8567+0.944≈1.80米
約 1.80 米，比父母平均身高 1.83 米矮，同樣符合 “向均值回歸” 規律（人類平均身高約 1.75 米）。

3.3 回歸分析的 “進化”：從身高到更廣泛的預測

高爾頓的身高遺傳研究，本質上是 “用線性關系描述兩個變量的預測關系”—— 這正是后來 “線性回歸” 的核心邏輯。隨著統計學的發展，回歸分析逐步突破了 “身高遺傳” 的局限，推廣到更多領域：

經濟學家用回歸分析預測 “GDP 與就業率的關系”；
農學家用回歸分析預測 “施肥量與農作物產量的關系”；
醫生用回歸分析預測 “血壓與年齡的關系”；
到了機器學習時代，回歸分析進一步升級，成為 “預測連續值” 的核心模型（如房價預測、銷量預測）。

可以說，高爾頓當年的一個簡單實驗，開啟了一門影響深遠的統計與機器學習分支。

四、回歸起源的核心啟示：對入門學生的 3 點啟發

了解回歸的起源，不僅是 “學歷史”，更能幫你理解回歸分析的本質，避免陷入 “只記公式不懂原理” 的誤區。對入門學生來說，有 3 點關鍵啟示：

4.1 回歸的本質：不是 “倒退”，而是 “規律”

很多人看到 “回歸” 就以為是 “回到過去”，其實不然 —— 回歸的核心是 “數據的統計規律”：極端值總會向均值靠攏，這是一種自然的統計現象，不是 “倒退”，而是 “穩定” 的體現。
比如考試成績：某次考 100 分（極端高分）的同學，下次可能考 90 分（向班級均值靠攏）；某次考 50 分（極端低分）的同學，下次可能考 60 分 —— 這不是 “退步” 或 “進步”，而是回歸規律的體現。

4.2 線性回歸的初心：用簡單模型描述復雜關系

高爾頓擬合的 “身高預測線”，是最簡單的線性模型 —— 只用一個一次函數，就描述了父母身高與子女身高的關系。這告訴我們：好的模型不一定復雜，能準確描述規律的簡單模型，往往更有價值。
入門階段學習線性回歸，就是要掌握 “用簡單線性關系解決預測問題” 的思維，這是后續學習復雜模型（如多項式回歸、神經網絡）的基礎。