1. 題意

給定一個 m x n 的矩陣，如果一個元素為 0 ，則將其所在行和列的所有元素都設為 0 。請使用 原地 算法。

2. 題解

想不到O(1)的空間復雜度的做法，

只有抄抄題解這樣子才能維持的了生活。

2.1 暴力

維護兩個標記數組，分別表示某行或者某列有0。

時間復雜度$O(n)$

空間復雜度$O(n)$

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {// row column flagint r = matrix.size();int c = 0;if ( r )c = matrix[0].size();vector<int> row_flags(r, 0);vector<int> col_flags(c, 0);for (int i = 0;i < r; ++i) {for (int j = 0;j < c; ++j) {if (0 == matrix[i][j]) {row_flags[i] = col_flags[j] = 1;}}}for (int i = 0;i < r; ++i) {for (int j = 0; j < c; ++j) {if (row_flags[i] || col_flags[j])matrix[i][j] = 0;}}}
};

2.2 原地算法

用數組的第一行和第一列分別來表示，某一列或者某一行它有0。

我們用0來表示有0，因為這樣就不用考慮第0行和第0列的情況了。

在用0行和第0列表示之前， 我們需要用兩個變量先預處理出第0行

和第0列的情況。

其實就是

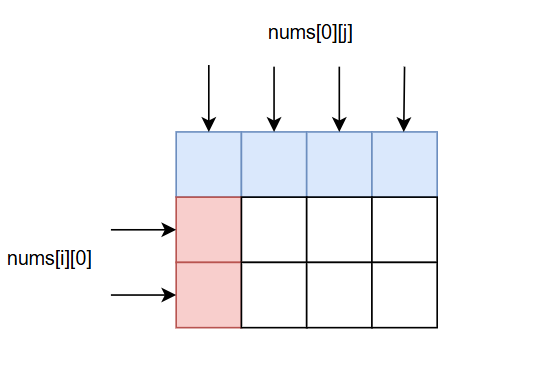
用nums[i][0]表示第i行有沒有0；

用nums[0][j]表示第j列有沒有0；

其中0<i<rows,0<j<cols

而第0行和第0列就用first_col first_rol單獨進行判斷了。

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {// row column flagint r = matrix.size();int c = 0;if ( 0 != r)c = matrix[0].size();int first_col = 0;int first_row = 0;for (int i = 0;i < c; ++i) {if ( matrix[0][i] == 0) {first_row = 1;break;}}for (int i = 0; i < r; ++i) {if ( matrix[i][0] == 0) {first_col = 1;break;}}for (int i = 1; i < r; ++i) {for (int j = 1; j < c; ++j) {if ( matrix[i][j] == 0) {matrix[0][j] = 0;matrix[i][0] = 0;}   }}for (int i = 1; i < r; ++i) {for (int j = 1; j < c; ++j) {if (matrix[0][j] == 0 || matrix[i][0] == 0)matrix[i][j] = 0;}}if (first_col) {for (int i = 0;i < r; ++i)matrix[i][0] = 0;}if (first_row) {for (int i = 0;i < c; ++i)matrix[0][i] = 0;}}
};

而題解中維護一個變量的做法，

其實就是把nums[0][0]這個位置再拿去

表示第0行有0或者第0列有0從而省略掉一個變量。

但這樣做其實增加了復雜度，以nums[0][0]表示第0列有無0來說。

對于nums[0][j]=0 , j>0來說，它不能引起nums[0][0]的更新，

因為nums[0][0]表示的是第0列的狀況，而不是第0行的狀況了。

因此需要加一個判斷了。

其次在最后遍歷數組的時候，我們需要逆序的列遍歷了。

因為如果順序的話nums[i][0]表示的行信息就被覆蓋掉了。

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {// row column flagint r = matrix.size();int c = 0;if ( 0 != r)c = matrix[0].size();int first_row = 0;for (int i = 0;i < c; ++i) {if ( matrix[0][i] == 0) {first_row = 1;break;}}for (int i = 0; i < r; ++i) {for (int j = 0; j < c; ++j) {if ( matrix[i][j] == 0) {matrix[0][j] = 0;if ( i != 0 )matrix[i][0] = 0;}   }}for (int i = 1; i < r; ++i) {// be carefull here, we need traversal reverse orderfor (int j = c - 1; ~j; --j) {if (matrix[0][j] == 0 || matrix[i][0] == 0)matrix[i][j] = 0;}}if (first_row) {for (int i = 0;i < c; ++i)matrix[0][i] = 0;}}
};

如果用nums[0][0]表示第0行的狀況也是相似的，代碼也給出來吧。

class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {// row column flagint r = matrix.size();int c = 0;if ( 0 != r)c = matrix[0].size();int first_col = 0;for (int i = 0;i < r; ++i) {if ( matrix[i][0] == 0) {first_col = 1;break;}}for (int i = 0; i < r; ++i) {for (int j = 0; j < c; ++j) {if ( matrix[i][j] == 0) {matrix[i][0] = 0;if (j != 0)matrix[0][j] = 0;}   }}for (int i = r - 1; ~i; --i) {for (int j = 1;j < c; ++j) {if ( matrix[0][j] == 0 || matrix[i][0] == 0 ) {matrix[i][j] = 0;}}}if (first_col) {for (int i = 0;i < r; ++i)matrix[i][0] = 0;}}
};

空間復雜度$O(1)$

3. 參考

leetcode