一、樹的基本概念
(一)定義
樹是由?n(n ≥ 0)?個結點組成的有限集合,是一種非線性層次結構:
- 當?
n = 0?時,稱為空樹; - 當?
n > 0?時,存在唯一的根結點(無前驅結點),其余結點可劃分為?m(m ≥ 0)?個互不相交的有限子集,每個子集都是一棵獨立的子樹。
(二)結點與樹的核心屬性
| 概念 | 定義 |
|---|---|
| 結點的度 | 結點擁有的子樹個數 |
| 葉結點(終端結點) | 度為 0 的結點(無子樹,位于樹的最底層) |
| 分支結點(非終端結點) | 度不為 0 的結點(至少擁有一棵子樹) |
| 樹的度 | 樹中所有結點的最大度數 |
| 深度 / 高度 | 從根結點開始計數,根為第 1 層,子結點依次遞增,樹的最大層數即為深度 / 高度 |
(三)存儲結構
- 順序存儲:通過數組存儲結點,需結合結點間的層次關系(如雙親下標)關聯數據,適用于結構規則的樹(如完全二叉樹)。
- 鏈式存儲:通過指針記錄結點的子樹地址(如孩子指針、兄弟指針),靈活性高,適用于各類形態的樹。
二、二叉樹的基本概念
(一)定義
二叉樹是?n(n ≥ 0)?個結點的有限集合,滿足:
- 當?
n = 0?時,為空二叉樹; - 當?
n > 0?時,由根結點、左子樹和右子樹組成,且左、右子樹互不相交,均為二叉樹。
(二)核心特點
- 每個結點最多有 2 棵子樹(左子樹和右子樹),即二叉樹的度最大為 2;
- 左、右子樹具有有序性,不可隨意顛倒(如 “僅有左子樹” 與 “僅有右子樹” 是兩種不同結構);
- 若結點僅有一棵子樹,必須明確標注是左子樹還是右子樹。
三、特殊二叉樹
| 類型 | 定義 |
|---|---|
| 斜樹 | 所有結點僅含一棵子樹,分為左斜樹(僅左子樹)和右斜樹(僅右子樹) |
| 滿二叉樹 | 深度為?k(k ≥ 1),所有分支結點均有左、右子樹,且所有葉子結點在同一層 |
| 完全二叉樹 | 深度為?k(k ≥ 1),按層序編號后,與同深度滿二叉樹的結點編號完全一致 |
四、二叉樹重要性質
- 第?
i?層結點數上限:第?i(i ≥ 1)?層最多有?2^{i-1}?個結點(如第 3 層最多 4 個結點); - 深度為?
k?的結點總數上限:深度為?k(k ≥ 1)?的二叉樹,最多有?2^k - 1?個結點(此時為滿二叉樹); - 葉子結點與度為 2 的結點關系:任意非空二叉樹中,葉子結點數?
n??= 度為 2 的結點數?n??+ 1(即?n? = n? + 1); - 完全二叉樹深度計算:含?
n?個結點的完全二叉樹,深度為??log?n? + 1(?x??表示向下取整)。
五、二叉樹遍歷方式
二叉樹遍歷是按規則訪問所有結點(每個結點僅訪問一次),核心分為深度優先遍歷(DFS)和廣度優先遍歷(BFS):
| 遍歷類型 | 具體方式 | 遍歷順序 |
|---|---|---|
| 深度優先遍歷 | 前序遍歷 | 根結點 → 左子樹 → 右子樹 |
| 中序遍歷 | 左子樹 → 根結點 → 右子樹 | |
| 后序遍歷 | 左子樹 → 右子樹 → 根結點 | |
| 廣度優先遍歷 | 層序遍歷 | 按層次從上到下、同層從左到右 |
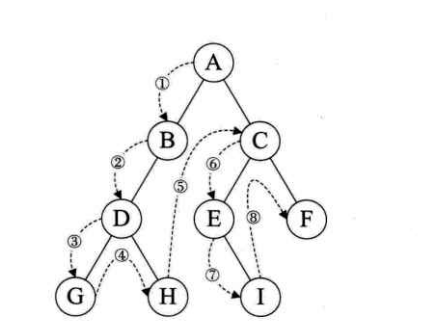
前序遍歷
規則是若二叉樹為空,則空操作返回,否則先訪問根結點,然后前序遍歷左子
樹,再前序遍歷右子樹。如圖,遍歷的順序為:ABDGHCEIF。
void PreOrder(TreeNode* root) {if (root == NULL) return; // 空樹,遞歸終止printf("%d ", root->data); // 訪問根結點PreOrder(root->left); // 遞歸遍歷左子樹PreOrder(root->right); // 遞歸遍歷右子樹
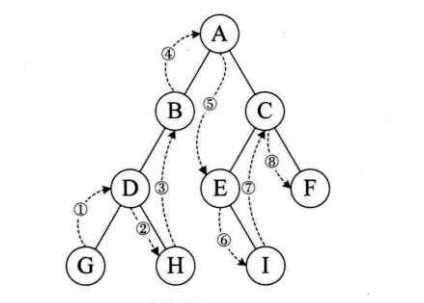
}中序遍歷
規則是若樹為空,則空操作返回,否則從根結點開始(注意并不是先訪問根結
點),中序遍歷根結點的左子樹,然后是訪問根結點,最后中序遍歷右子樹。如圖,遍歷的順序為:GDHBAEICF。
void InOrder(TreeNode* root) {if (root == NULL) return; // 空樹,遞歸終止InOrder(root->left); // 遞歸遍歷左子樹printf("%d ", root->data); // 訪問根結點InOrder(root->right); // 遞歸遍歷右子樹
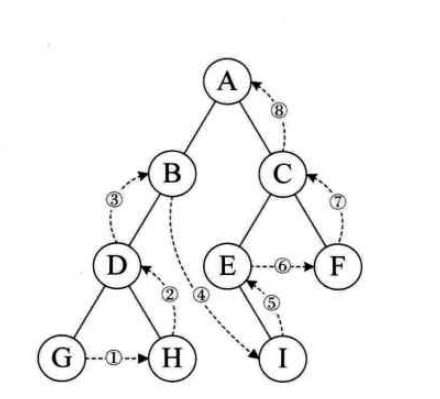
}3.后序遍歷
規則是若樹為空,則空操作返回,否則從左到右先葉子后結點的方式遍歷訪問左
右子樹,最后是訪問根結點。如圖,遍歷的順序為:GHDBIEFCA。
void PostOrder(TreeNode* root) {if (root == NULL) return; // 空樹,遞歸終止PostOrder(root->left); // 遞歸遍歷左子樹PostOrder(root->right); // 遞歸遍歷右子樹printf("%d ", root->data); // 訪問根結點
}遍歷順序:按樹的層次從上到下、同一層從左到右依次訪問所有結點,本質是 “按層訪問”。?實現依賴:需借助隊列(先進先出,FIFO),通過 “根結點入隊 → 隊頭出隊訪問 → 左右子結點入隊 → 循環至隊空” 的邏輯實現。
void LevelOrder(TreeNode* root) {if (root == NULL) return; // 空樹,直接返回SeqQue* queue = CreateSeqQue(100); // 創建容量為 100 的隊列EnterSeqQue(queue, root); // 根結點入隊while (!IsEmptySeqQue(queue)) { // 隊列非空,循環處理TreeNode* curr = GetHeadSeqQue(queue); // 取隊頭結點printf("%d ", curr->data); // 訪問當前結點QuitSeqQue(queue); // 隊頭結點出隊if (curr->left != NULL) // 左子結點非空,入隊EnterSeqQue(queue, curr->left);if (curr->right != NULL) // 右子結點非空,入隊EnterSeqQue(queue, curr->right);}DestroySeqQue(queue); // 銷毀隊列,釋放內存
}






:『SRE對智能運維領域所產生的深遠影響』)








)
在 BLE 中的應用:建立、流控與數據傳輸)
)
