計算機內存中的整型存儲奧秘、大小端字節序及其判斷方法

一、回顧與引入：整數在內存中的存儲方式

為什么要采用補碼存儲？

二、大小端字節序及其判斷方法

1、什么是大小端？

2、為什么存在大小端？

3、練習

練習1：簡述大小端概念并設計判斷程序（百度面試題）

參考代碼1：

關鍵原理：字節序（Endianness）

小端模式（Little-endian）

大端模式（Big-endian）

check_sys()?函數詳解

結果分析

參考代碼2（使用聯合體）：

聯合體（union）的特性

內存布局分析

小端模式

大端模式

工作原理

練習2：有符號與無符號字符型的輸出

1. 變量聲明和初始化

2. 初始化時的賦值

3.?printf?輸出

4. 具體每個變量的提升和輸出

5. 最終輸出

注意：char?的符號性

練習3：字符型變量以無符號格式輸出

1. 變量?a?的聲明和初始化

2.?printf?格式化輸出

3. 不匹配的格式說明符

4. 實際輸出（在常見的二進制補碼系統中）

5. 另一種理解（直接從char到unsigned int的轉換）（了解即可）

6. 總結輸出

7. 最終答案

1. 變量?a?的聲明和初始化

2. 有符號char的溢出行為

3.?printf?格式化輸出

4. 類型不匹配的后果

5. 實際輸出計算（在32位系統，二進制補碼）

6. 另一種理解方式

7. 如果char是無符號的？

8. 最終輸出

練習4：字符數組與strlen

練習5：無符號變量的循環

問題原因

練習6：指針運算與字節序（x86小端模式）

代碼分析

1.?ptr1[-1]?的值

2.?*ptr2?的值（小端序假設）

輸出

注意

總結

一、回顧與引入：整數在內存中的存儲方式

在介紹strlen操作符時，我們已經提到過以下內容：

整數的二進制表示方法有三種，分別是原碼、反碼和補碼。

????????對于有符號整數，三種表示方法都包含符號位和數值位兩個部分。符號位以“0”表示正數，“1”表示負數，通常位于最高位，其余部分為數值位。

正整數的原碼、反碼和補碼完全相同。
負整數的原碼、反碼和補碼則各不相同。

具體轉換方式如下：

原碼：直接根據數值的正負形式翻譯成二進制表示。
反碼：在原碼的基礎上，保持符號位不變，其余各位按位取反。
補碼：在反碼的基礎上加 1 得到。

對于整型數據，其在內存中實際存儲的是二進制補碼形式。

為什么要采用補碼存儲？

在計算機系統中，數值一律采用補碼來表示和存儲，主要原因包括：

使用補碼可以統一處理符號位與數值部分，簡化硬件設計；
補碼能夠將加法和減法運算統一為加法操作（CPU 通常只內置加法器）；
補碼與原碼之間的轉換過程一致，無需額外的硬件電路支持，提高了計算效率并降低了系統復雜度。

二、大小端字節序及其判斷方法

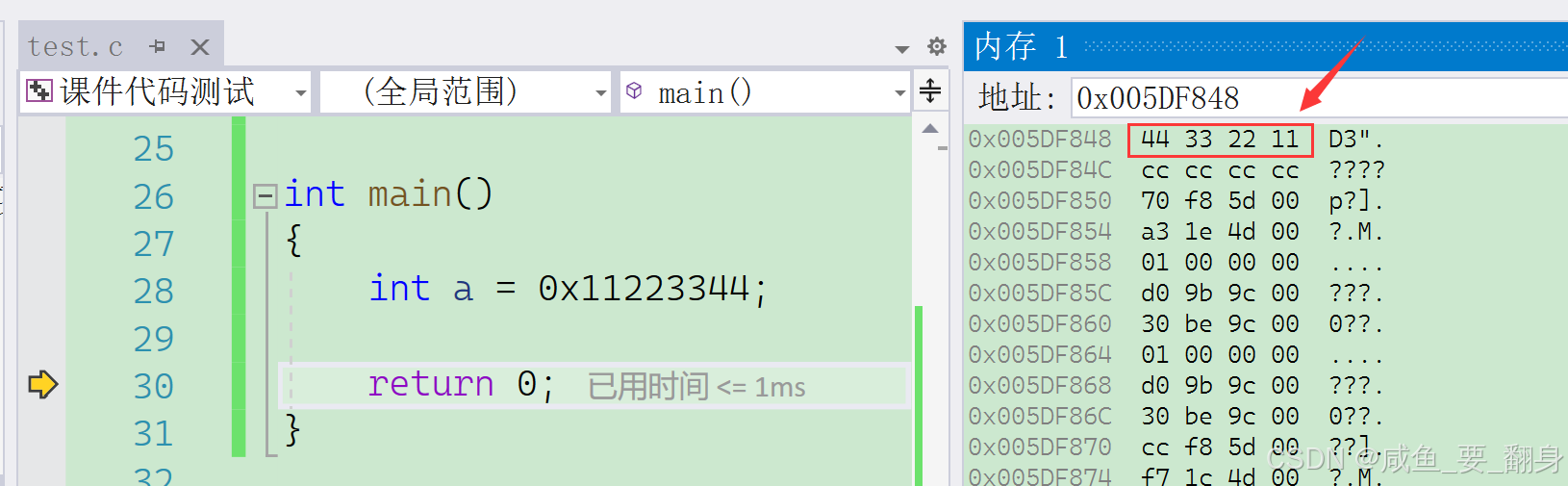
在我們了解整數在內存中的存儲方式后，通過以下代碼調試可以觀察到一個現象：

#include <stdio.h>
int main()
{int a = 0x11223344;return 0;
}

????????調試時會發現，變量?a?中的值?0x11223344?在內存中是以字節為單位倒序存儲的。為什么會這樣呢？

1、什么是大小端？

????????當一個數據超過一個字節時，在內存中的存儲順序就涉及字節序的問題。根據不同的存儲順序，可分為大端字節序（Big-Endian）和小端字節序（Little-Endian）。其具體定義為：

大端模式：數據的低位字節（即權值較小的字節）保存在內存的高地址處，而數據的高位字節保存在內存的低地址處。
小端模式：數據的低位字節保存在內存的低地址處，而數據的高位字節保存在內存的高地址處。

理解并記住這兩種模式有助于我們在不同平臺或網絡傳輸中正確處理多字節數據。

2、為什么存在大小端？

????????計算機系統中以字節為單位編址，每個地址對應一個字節（8 bit）。但在C語言中，除了?char（8 bit）外，還有?short（16 bit）、int?和?long（32 bit 或更長，取決于編譯器和架構）等類型。對于寄存器寬度大于8位的處理器（如16位或32位CPU），如何排列多個字節就成為一個必須解決的問題，因此出現了大端和小端兩種存儲模式。

????????舉例來說，一個16位的變量?short x，其地址為?0x0010，值為?0x1122。其中?0x11?是高字節，0x22?是低字節。在大端模式下，0x11?存放在?0x0010（低地址），0x22?存放在?0x0011（高地址）；小端模式則相反。常見的x86架構為小端模式，而KEIL C51通常為大端模式。許多ARM和DSP處理器默認為小端模式，部分ARM處理器還支持通過硬件配置選擇字節序。

3、練習

練習1：簡述大小端概念并設計判斷程序（百度面試題）

要求：簡述大端和小端字節序的概念，并編寫程序判斷當前機器的字節序。

參考代碼1：

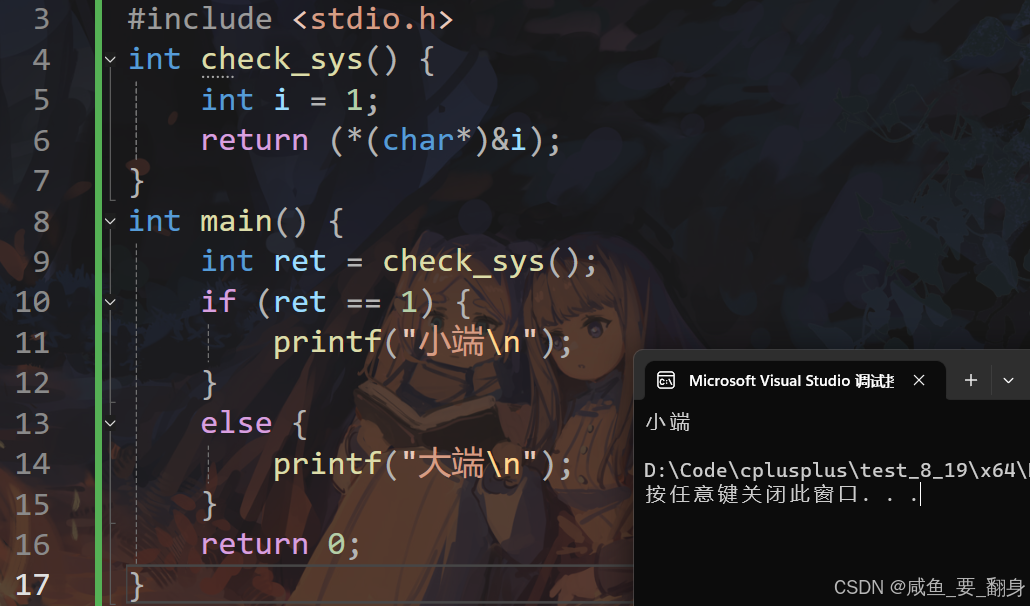
#include <stdio.h>
int check_sys() {int i = 1;return (*(char *)&i);
}
int main() {int ret = check_sys();if(ret == 1) {printf("小端\n");} else {printf("大端\n");}return 0;
}

關鍵原理：字節序（Endianness）

小端模式（Little-endian）

低位字節存儲在低地址
對于整數?1（0x00000001）：
- 內存布局（地址從低到高）：01 00 00 00

大端模式（Big-endian）

高位字節存儲在低地址
對于整數?1（0x00000001）：
- 內存布局（地址從低到高）：00 00 00 01

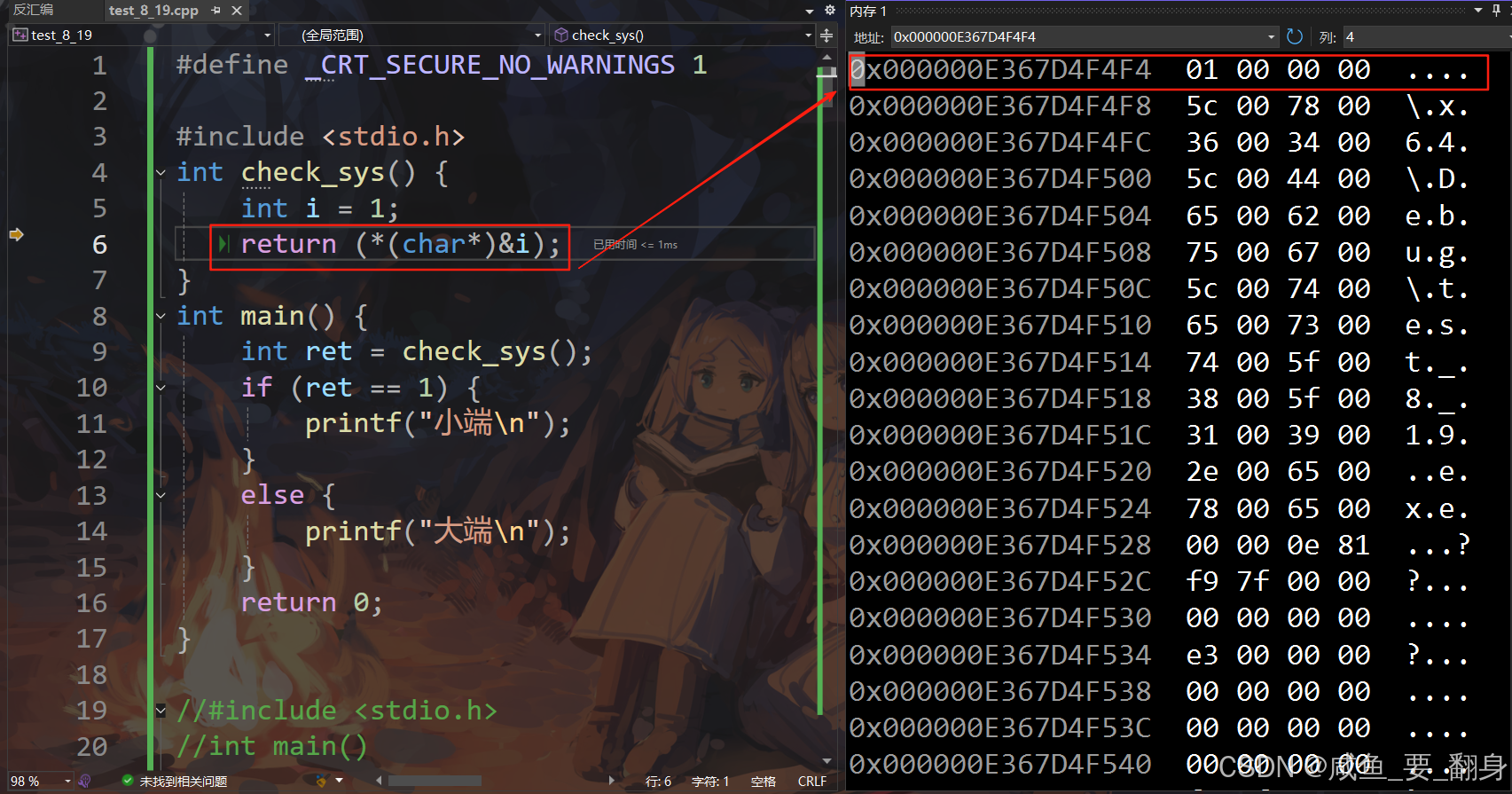
`check_sys()`?函數詳解

int i = 1;在內存中分配4字節空間存儲整數1
&i獲取變量i的起始地址（最低字節的地址）
(char *)&i
- 將int指針強制轉換為char指針
- char指針指向內存的第一個字節
*(char *)&i解引用char指針，獲取第一個字節的值

結果分析

小端系統：第一個字節是?0x01，返回1
大端系統：第一個字節是?0x00，返回0

參考代碼2（使用聯合體）：

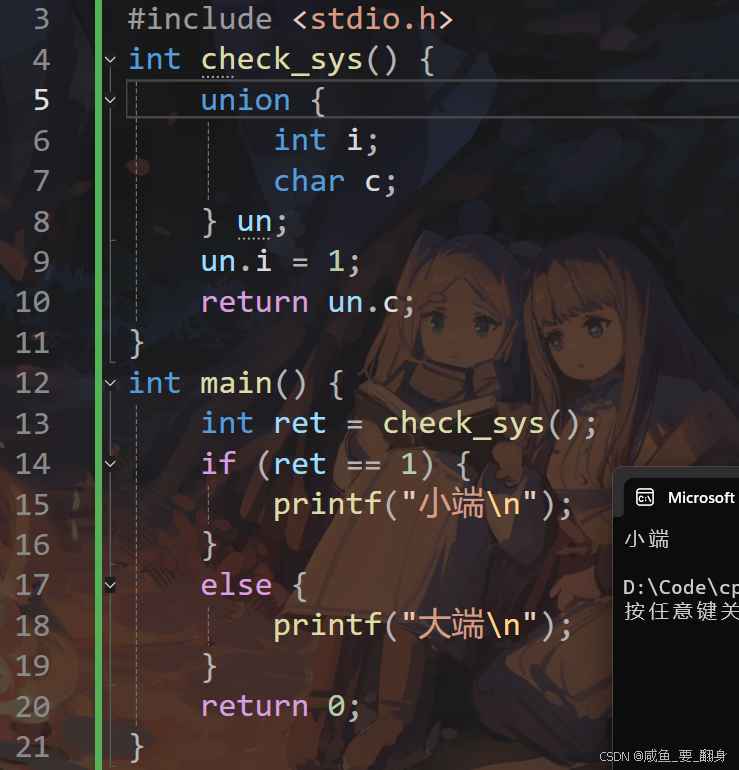
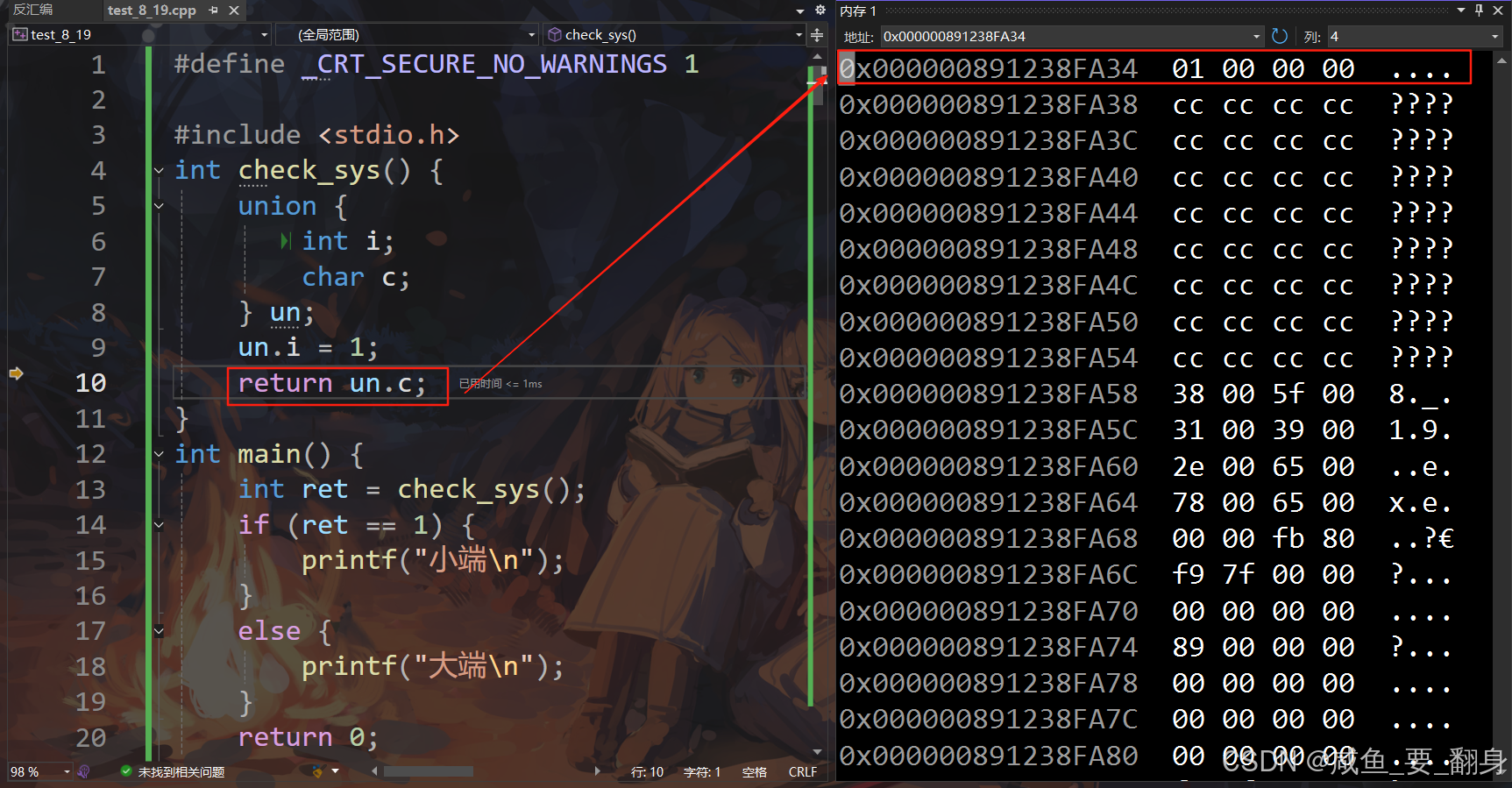
int check_sys() {union {int i;char c;} un;un.i = 1;return un.c;
}

聯合體（union）的特性

聯合體的所有成員共享同一塊內存空間
大小由最大的成員決定（這里int通常是4字節，char是1字節）
對任何一個成員的修改都會影響其他成員的值

內存布局分析

當?un.i = 1?時：

整數?1?的十六進制表示為：0x00000001
在聯合體的共享內存中存儲這個值

小端模式

內存地址（低→高）： 0x00  0x01  0x02  0x03
存儲數據：         0x01  0x00  0x00  0x00↑ 最低地址存儲最低有效字節

大端模式

內存地址（低→高）： 0x00  0x01  0x02  0x03
存儲數據：         0x00  0x00  0x00  0x01↑ 最低地址存儲最高有效字節

工作原理

un.i = 1：將整數1存入聯合體的4字節空間
un.c：訪問聯合體的第一個字節（最低地址）
- 小端：第一個字節是?0x01?→ 返回1
- 大端：第一個字節是?0x00?→ 返回0

練習2：有符號與無符號字符型的輸出

#include <stdio.h>
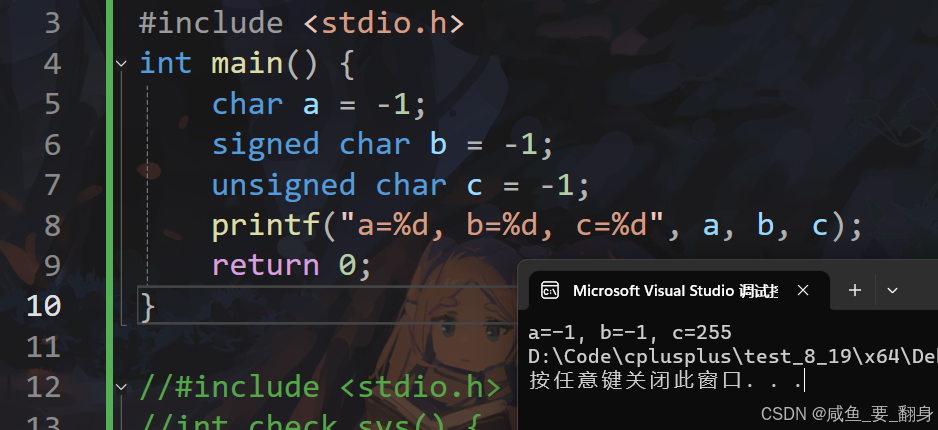
int main() {char a = -1;signed char b = -1;unsigned char c = -1;printf("a=%d, b=%d, c=%d", a, b, c);return 0;
}

1. 變量聲明和初始化

char a = -1;在大多數系統中，char?默認是有符號的（相當于?signed char），但這一點取決于編譯器和平臺。通常，char?可以是有符號或無符號的，但常見的是有符號的。這里我們假設?char?是有符號的（如大多數x86系統）。
signed char b = -1;明確聲明為有符號字符，初始化為 -1。
unsigned char c = -1;無符號字符類型，初始化為 -1。

2. 初始化時的賦值

對于有符號類型（a?和?b），-1 可以直接表示（二進制補碼形式）。
對于無符號類型（c），初始化賦值為 -1。由于無符號類型不能表示負數，所以會發生轉換：-1 會被轉換為無符號類型所允許的最大值（因為無符號類型是模運算）。
具體來說，對于?unsigned char（通常是8位），范圍是 0 到 255。
-1 的二進制補碼表示是?11111111（所有位為1），當解釋為無符號時，就是 255。

3.?`printf`?輸出

printf?使用?%d?格式化輸出，它期望的是?int?類型參數。
所以?a,?b,?c?都會先被提升為?int?類型（整數提升），然后傳遞給?printf。
整數提升規則：
- 對于有符號類型（如?signed char），提升時進行符號擴展（即高位填充符號位）。
- 對于無符號類型（如?unsigned char），提升時高位填充0。

4. 具體每個變量的提升和輸出

a（假設是有符號 char）：
- 初始值：-1（二進制?11111111）
- 提升為?int：符號擴展，高位全填1（即?11111111 11111111 11111111 11111111），這仍然是 -1。
- 輸出：a=-1
b（signed char）：
- 與?a?相同：-1（二進制?11111111）
- 提升為?int：符號擴展，得到 -1。
- 輸出：b=-1
c（unsigned char）：
- 初始值：-1 被轉換為無符號值 255（二進制?11111111）。
- 提升為?int：因為是無符號，高位填充0（即?00000000 00000000 00000000 11111111），所以是 255。
- 輸出：c=255

5. 最終輸出

因此，輸出為：a=-1, b=-1, c=255

注意：`char`?的符號性

????????如果系統默認將?char?定義為無符號（如某些ARM編譯器），那么?a?的行為會與?c?相同（輸出255）。但常見情況下（如GCC在x86上），char?是有符號的，所以輸出為 -1。

練習3：字符型變量以無符號格式輸出

#include <stdio.h>
int main() {char a = -128;printf("%u\n", a);return 0;
}

1. 變量?`a`?的聲明和初始化

char a = -128;：這里聲明了一個char類型的變量a，并初始化為-128。
在大多數系統中，char默認是有符號的（signed char），其范圍通常是-128到127（假設是8位二進制補碼表示）。
-128正好是char類型能表示的最小值（二進制表示為10000000）。

2.?`printf`?格式化輸出

printf("%u\n", a);：這里使用%u格式說明符來輸出a的值。%u用于輸出無符號十進制整數。
但注意：a是char類型（本質上是一個整數類型），當傳遞給printf時，由于可變參數函數的默認參數提升規則（default argument promotion），a會被提升為int類型（因為char是比int更小的整數類型）。
- 具體來說：char（無論是signed char還是unsigned char）在傳遞給可變參數函數（如printf）時，會被提升為int（如果int可以表示所有char的值）或unsigned int（但通常int可以表示）。
- 對于有符號的char a = -128，提升為int后仍然是-128（因為int可以表示-128）。

3. 不匹配的格式說明符

%u期望一個unsigned int類型的參數，但實際傳遞的是int類型的-128（由于提升）。
這會導致未定義行為（undefined behavior），因為C標準規定：如果格式說明符和實際參數類型不匹配，行為是未定義的。
然而，在大多數實現中，會直接按位解釋（即：將傳遞的int類型的二進制表示直接當作unsigned int來解讀）。

4. 實際輸出（在常見的二進制補碼系統中）

a的原始值（char類型）是-128，其二進制表示（8位）是：10000000。
當提升為int時（假設32位int），由于符號擴展，-128的int表示是：二進制：11111111 11111111 11111111 10000000（即全1填充到最高位，直到第8位為1，其余低位為0）。
當用%u解釋這個int值時（即把相同的二進制位模式當作無符號整數），得到的無符號整數值是：
- 11111111 11111111 11111111 10000000（二進制） =?4294967168（十進制）。
- 計算：最高位是1，所以這是一個很大的正數（2^32 - 128 = 4294967168）。

5. 另一種理解（直接從`char`到`unsigned int`的轉換）（了解即可）

實際上，在傳遞過程中，char先被提升為int（值為-128），然后被printf用%u解讀（即強制轉換為unsigned int）。
有符號整數到無符號整數的轉換規則：C標準規定，如果源值是負數，則轉換結果為“該值加上無符號類型最大值加1”（即模運算）。
- 所以，(unsigned int)(-128)?=?-128 + UINT_MAX + 1?=?UINT_MAX - 127。
- 在32位系統中，UINT_MAX是4294967295，所以結果是4294967295 - 127 = 4294967168。

6. 總結輸出

因此，在常見的系統（32位，二進制補碼）上，輸出將是4294967168。
注意：如果char是無符號的（某些系統可能定義char為unsigned char），那么a = -128實際上會賦值128（因為無符號char的范圍是0-255），但這里我們假設char是有符號的（這是大多數系統的默認行為）。

7. 最終答案

所以，這段代碼的輸出是：

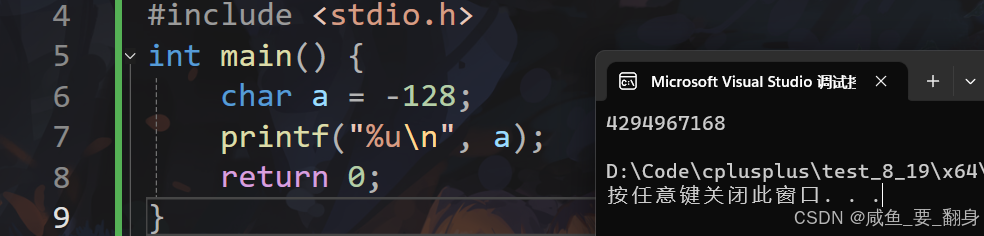
#include <stdio.h>
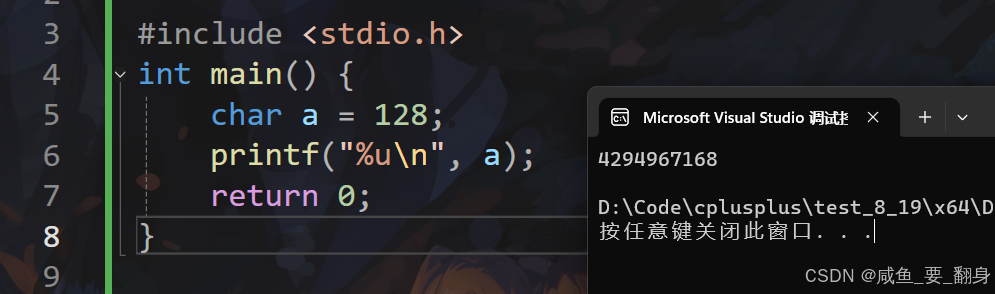
int main() {char a = 128;printf("%u\n", a);return 0;
}

1. 變量?`a`?的聲明和初始化

char a = 128;：聲明了一個char類型的變量a，并初始化為128。
在大多數系統中，char默認是有符號的（signed char），其范圍是-128到127（8位二進制補碼表示）。
128超出了signed char的正數范圍（127是最大值），所以這里會發生整數溢出。

2. 有符號char的溢出行為

在C語言中，有符號整數溢出是未定義行為（undefined behavior）。
但在大多數實現（使用二進制補碼）中，數值會"環繞"（wrap around）：
- 127（01111111） + 1 =?-128（10000000）
- 所以?128?會被解釋為?-128（因為128 = 127 + 1）

3.?`printf`?格式化輸出

printf("%u\n", a);：使用%u格式說明符輸出a的值。
由于可變參數函數的默認參數提升規則，char類型的a會被提升為int類型。
%u期望一個unsigned int類型的參數，但實際傳遞的是提升后的int類型值（-128）。

4. 類型不匹配的后果

這是未定義行為，因為格式說明符%u與實際參數類型（int）不匹配。
但在大多數系統中，會直接按位解釋（將int的二進制表示當作unsigned int來解讀）。

5. 實際輸出計算（在32位系統，二進制補碼）

a的實際值：由于溢出，a = 128?被存儲為?-128（二進制：10000000）
提升為int：-128?的32位二進制補碼表示是：11111111 11111111 11111111 10000000
當用%u解釋這個位模式時，被當作無符號整數：
- 二進制：11111111 11111111 11111111 10000000
- 十進制值：232 - 128 = 4294967296 - 128 = 4294967168

6. 另一種理解方式

從有符號到無符號的轉換規則：(unsigned int)(-128) = -128 + UINT_MAX + 1
在32位系統中，UINT_MAX = 4294967295
所以：4294967295 + 1 - 128 = 4294967168

7. 如果char是無符號的？

如果系統默認char是unsigned char（范圍0-255），那么：
- a = 128?是有效的
- 提升為int時是128（正數）
- 用%u輸出：128
但大多數系統（如x86）默認char是有符號的。

8. 最終輸出

在常見的系統（32位，二進制補碼，char有符號）上，輸出為：

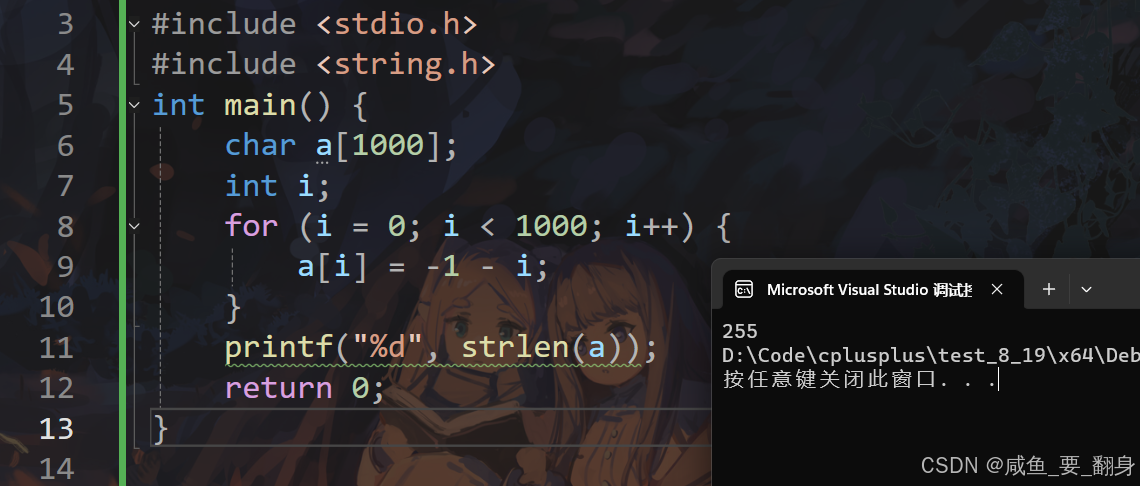
練習4：字符數組與strlen

#include <stdio.h>
#include <string.h>
int main() {char a[1000];int i;for(i = 0; i < 1000; i++) {a[i] = -1 - i;}printf("%d", strlen(a));return 0;
}

數組?a?的初始化：
- a?是一個長度為1000的字符數組（char類型，在大多數系統中是有符號的，范圍是-128到127）。
- 循環中，a[i] = -1 - i?對每個元素賦值。
  - 當?i=0：a[0] = -1 - 0 = -1
  - 當?i=1：a[1] = -1 - 1 = -2
  - ...
  - 當?i=127：a[127] = -1 - 127 = -128（這是char能表示的最小值）
  - 當?i=128：a[128] = -1 - 128 = -129，但char只能表示-128到127，所以會發生溢出。
    - 在補碼表示中，-129的二進制是（假設8位char）：-129的補碼是（超出8位范圍），實際會截斷為8位。
    - 計算：-129的二進制（16位表示）是1111111101111111，截取低8位是01111111（即127）。
    - 類似地，-130截斷為126，依此類推。
????????實際上，我們可以用取模的方式來計算溢出后的值（因為C標準規定有符號整數溢出是未定義行為，但通常實現是環繞的）：
- 對于有符號char，值會以256為模環繞（因為8位有符號數的表示范圍是-128~127，共256個值）。
- 所以，-1 - i?的實際值可以通過?(-1 - i) % 256?來得到（但需要調整到在-128~127之間）。
更直接的方式是考慮序列：
- i=0: -1
- i=1: -2
- ...
- i=127: -128
- i=128: -129 -> 由于溢出，實際為127（因為-129 + 256 = 127）
- i=129: -130 -> 126
- ...
- i=255: -256 -> 0
- i=256: -257 -> -1（因為-257 + 256*2 = 255？不對，實際上應該模256，但注意有符號數的表示）
實際上，我們可以寫出前幾個值：
i: 0 1 2 ... 127 128 129 130 ... 255 256 ...
a[i]: -1, -2, -3 ... -128,127,126,125 ... 0, -1, ...

????????注意，當i=255時：-1-255 = -256，模256后是0（因為-256正好是256的倍數，所以余0）。
????????當i=256時：-1-256=-257，模256：-257 % 256 = -1（因為-257 = -256*1 -1，所以余-1？但實際在8位中，它表示成-1）。

????????但這里我們不需要所有值，我們只需要知道第一個0出現在哪里？因為strlen計算的是從開始到第一個'\0'（即0）的字符數。
strlen的工作：strlen(a)?從a[0]開始掃描，直到遇到第一個值為0的字節（即'\0'），然后返回之前的字符個數（不包括0本身）。
尋找第一個0：
- 我們需要找到最小的i，使得a[i] == 0。
- 根據上面的賦值：a[i] = -1 - i。
- 設a[i] == 0，即-1 - i == 0？但這樣i=-1，顯然不對（因為i從0開始）。
- 實際上，由于溢出，我們需要解方程：(-1 - i) mod 256 = 0（即-1-i是256的倍數）。
- 即-1 - i = 256 * k（k為整數），因為值在0時停止。
- 取k=-1（因為i非負，所以k應為負）：-1 - i = -256?=>?i = 255。
  所以當i=255時，a[255] = -1-255 = -256，模256后為0（因為-256是256的整數倍，所以余0）。
因此，第一個0出現在索引255處。
驗證：
- i=255時：a[255] = -1-255 = -256。在8位有符號表示中，-256的二進制（補碼）本需要9位（100000000），截斷低8位后是00000000（即0）。
- 所以a[255] = 0。
strlen(a)的返回值：strlen從a[0]開始計數，直到a[254]（因為a[255]是0，不計入），所以總共255個字符。

因此，程序輸出的是255。

練習5：無符號變量的循環

#include <stdio.h>
unsigned char i = 0;
int main() {for(i = 0; i <= 255; i++) {printf("hello world\n");}return 0;
}

問題原因

unsigned char i?的范圍是 0 到 255（8位無符號字符）
當?i?增加到 255 后，執行?i++?會導致整數溢出
在無符號整型中，溢出會回繞：255 + 1 = 0
因此條件?i <= 255?永遠為真，循環永遠不會結束

#include <stdio.h>
int main() {unsigned int i;for(i = 9; i >= 0; i--) {printf("%u\n", i);}return 0;
}

問題原因

unsigned int i?是無符號整型，范圍是?0?到?UINT_MAX（通常是 0 到 4,294,967,295）
當?i = 0?時，執行?i--?會導致下溢
在無符號整型中，下溢會回繞：0 - 1 = UINT_MAX（非常大的正數）
因此條件?i >= 0?永遠為真（因為無符號數永遠 ≥ 0），循環永遠不會結束

練習6：指針運算與字節序（x86小端模式）

#include <stdio.h>
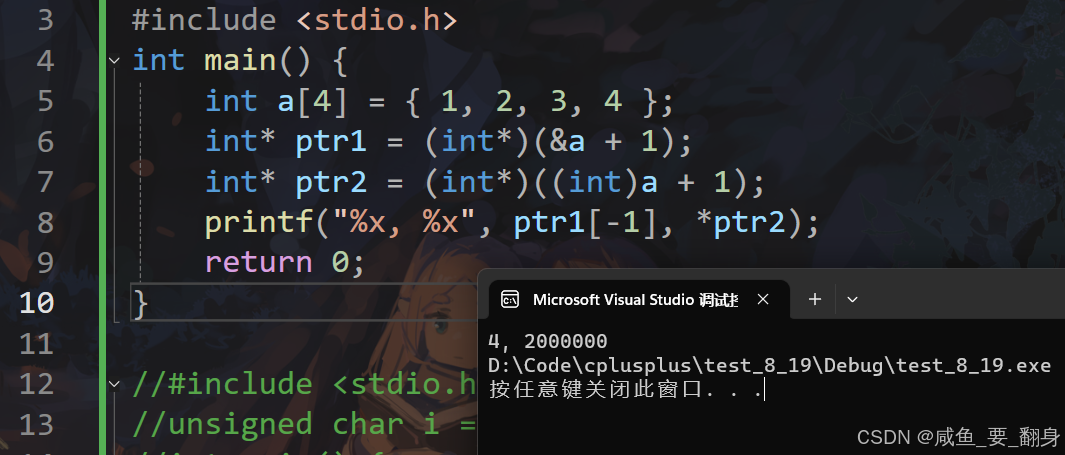
int main() {int a[4] = {1, 2, 3, 4};int *ptr1 = (int *)(&a + 1);int *ptr2 = (int *)((int)a + 1);printf("%x, %x", ptr1[-1], *ptr2);return 0;
}

????????這段代碼涉及指針運算和類型轉換，行為是未定義的（UB），但在小端序機器上可能有特定輸出。我們來分析：

代碼分析

int a[4] = {1, 2, 3, 4};
int *ptr1 = (int *)(&a + 1);      // 指向數組末尾之后
int *ptr2 = (int *)((int)a + 1);  // 將地址轉為整數加1再轉回指針
printf("%x, %x", ptr1[-1], *ptr2); // 輸出

1.?`ptr1[-1]`?的值

&a?是「指向整個數組的指針」，類型是?int (*)[4]
&a + 1?會跳過整個數組（16字節），指向數組末尾之后
(int *)?強制轉換為?int*，現在?ptr1?指向?a[4]（不存在）
ptr1[-1]?等價于?*(ptr1 - 1)，即從末尾回退一個int，指向?a[3]
所以?ptr1[-1]?是?4

2.?`*ptr2`?的值（小端序假設）

a?是數組首地址（假設為?0x1000）
(int)a?將地址轉為整數（假設?0x1000）
(int)a + 1?得到?0x1001
(int *)?再轉回指針，現在?ptr2?指向?0x1001（非對齊訪問，UB！）

在小端機器上，數組?a?在內存中的布局（每個int占4字節）：

地址      數據（字節序，小端）
0x1000:   01 00 00 00   // a[0] = 1
0x1004:   02 00 00 00   // a[1] = 2  
0x1008:   03 00 00 00   // a[2] = 3
0x100C:   04 00 00 00   // a[3] = 4

ptr2?指向?0x1001，會讀取從?0x1001?開始的4字節：