一、計數排序
計數排序又稱為鴿巢原理,是對哈希直接定址法的變形應用。操作步驟如下:①統計相同元素出現的次數? ②根據統計的結果將序列回收到原來的序列中
比如,現在有一個數組{6,1,2,9,4,2,4,1,4}。該數組中,元素1出現兩次,元素2出現兩次,元素4出現三次,元素6出現一次,元素9出現一次。我們這時就可以創建一個新數組,把原數組里的數據作為新數組的下標,原數組數據出現的次數作為新數組里下標對應的值,得到的新數組如下圖所示:

這時我們定義一個變量 i 遍歷 count 數組,如果count[i] 里的數據不為0,我們就循環向arr數組中插入count[i] 次,就可以得到排好序的數組,如下圖所示:

思路很簡單,但是新創建的count數組的大小如何確定呢?
在上面的示例中,我們似乎是找到了原數組中的最大值9,然后給count數組開辟了0~9共10個空間,那么是不是這樣開辟空間大小就行呢?假如現在有一個數組{100,101,109,105,101,105},如果我們還像剛才那樣開辟0~109共110個空間,那么count數組中下標為0~99這100個空間就嚴重浪費了。所以原數組中找最大值,再讓最大值+1這個方法是錯誤的,可能會造成空間浪費。那該怎么做呢?我們還拿{100,101,109,105,101,105}這個數組為例,最大值max = 109,最小值min =100,100~109之間最多有10個數據,也就是說count數組所需的最大空間就是10,所以我們用max - min + 1就可以得到count數組的空間大小了。
注:計數排序在數據范圍集中時效率很高,但是適用范圍及場景有限!
代碼如下:
//計數排序
void CountSort(int* arr, int n)
{//找最大和最小值int min = arr[0], max = arr[0];for (int i = 1;i < n;i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}// max - min + 1 確定count數組大小int range = max - min + 1;int* count = (int*)malloc(range * sizeof(int));if (count == NULL){perror("malloc fail");exit(1);}//初始化memset(count, 0, range * sizeof(int));for (int i = 0;i < n;i++){count[arr[i] - min]++;}//將count數組還原到原數組中,使其有序int index = 0;for (int i = 0;i < range;i++){while (count[i]--){arr[index++] = min + i;}}
}計數排序時間復雜度為O(N + range)
穩定性:穩定
二、排序算法的穩定性分析
穩定性:假設在待排序的序列中,存在多個具有相同關鍵字的記錄,經過排序,這些記錄的相對次序保持不變。即在原序列中,r[i] == r[j],且r[i] 在 r[j] 之前,而排序后的序列,r[i] 仍在 r[j] 之前,則稱這種排序算法是穩定的。

下面給出七種排序算法的時間復雜度和穩定性:
| 排序方法 | 時間復雜度 | 穩定性 |
| 冒泡排序 | O(n^2) | 穩定 |
| 直接選擇排序 | O(n^2) | 不穩定 |
| 直接插入排序 | O(n^2) | 穩定 |
| 希爾排序 | O(nlogn)~O(n^2) | 不穩定 |
| 堆排序 | O(nlogn) | 不穩定 |
| 歸并排序 | O(nlogn) | 穩定 |
| 快速排序 | O(nlogn) | 不穩定 |
三、快速排序 拓展
快速排序最核心的一點在于基準值的確定。關于如何找基準值,我們在上一章講了三種方法。但是,當待排序數組中含有大量重復數據時,再使用之前的方法會讓快速排序的時間復雜度接近于O(n^2)。因此,這里分享兩種優化方法。
1、三路劃分
三路劃分,顧名思義,就是把數組劃分成三個區間。把重復的相等的數據集中在中間,左邊就是較小值,右邊就是較大值。方法如下圖所示:

根據上述的方法思路,我們來模擬實現一下該流程:
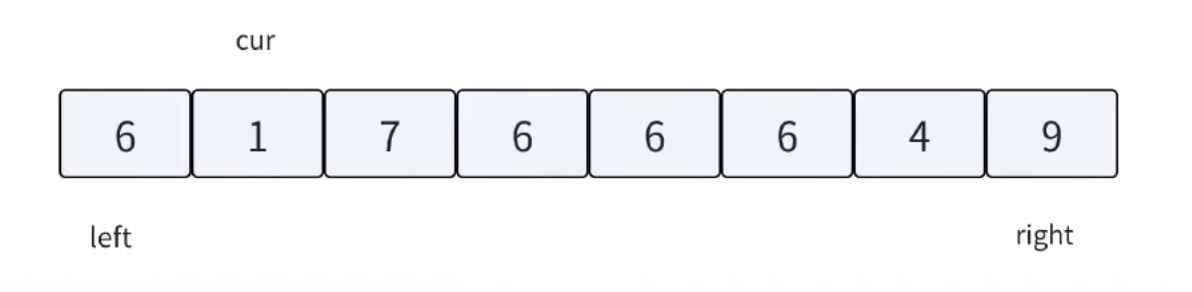
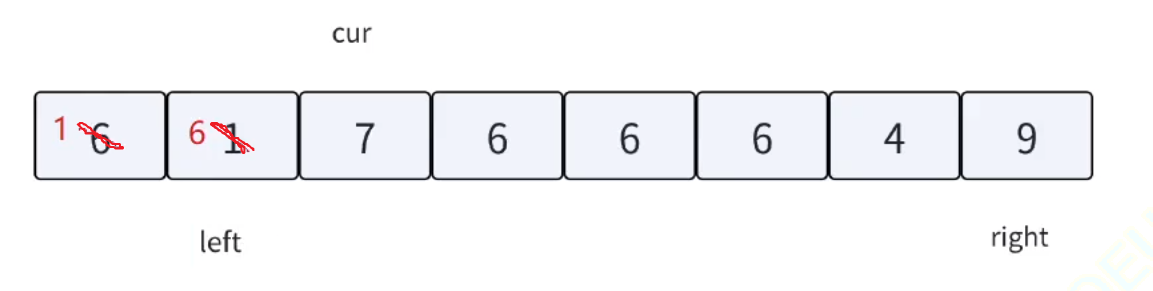
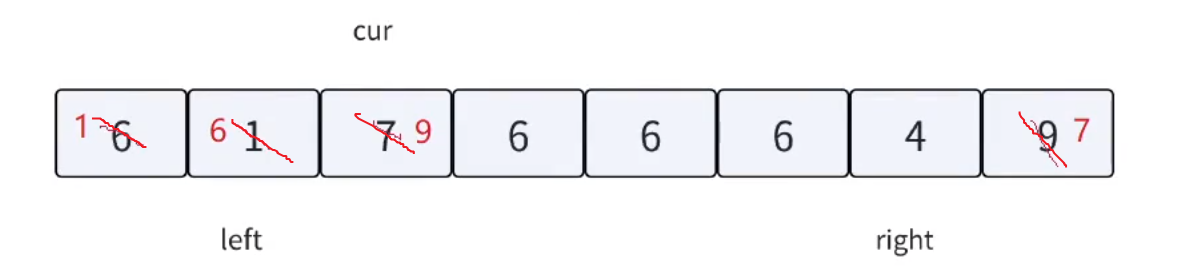
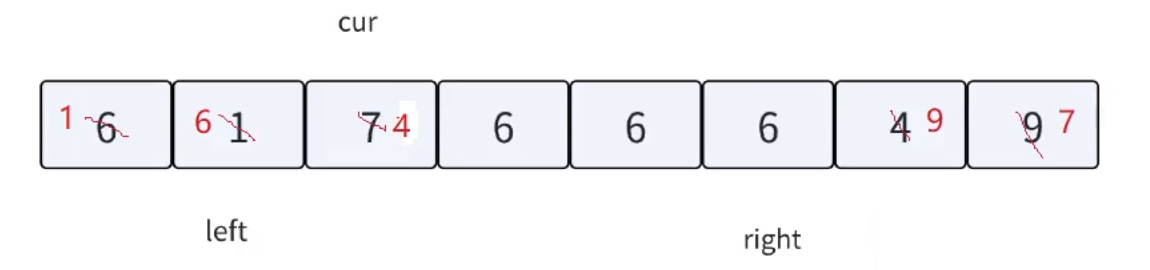
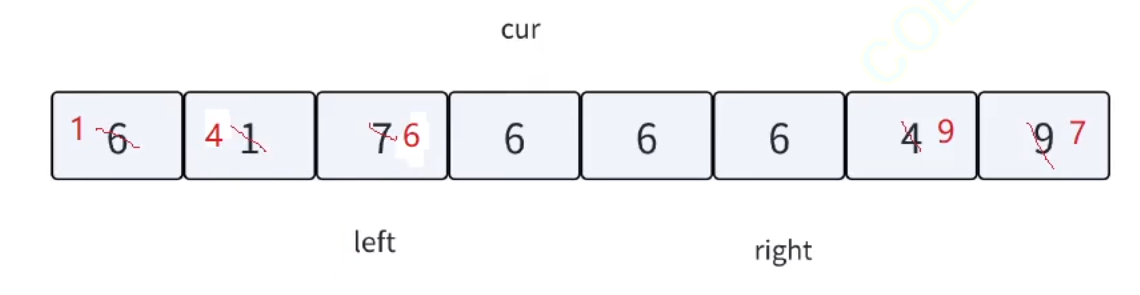
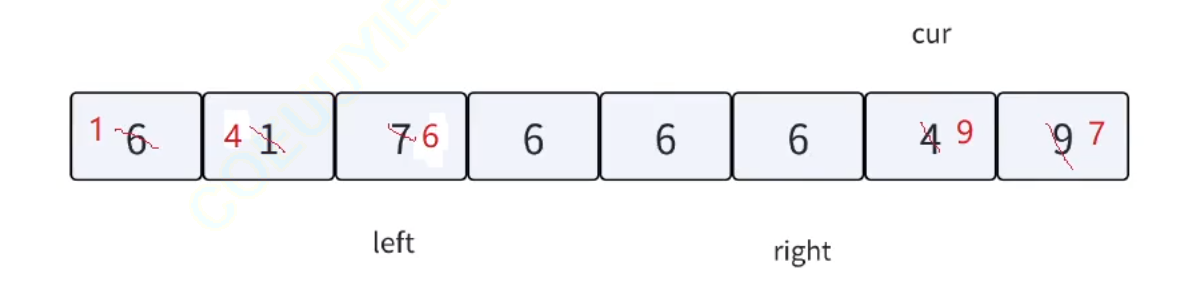
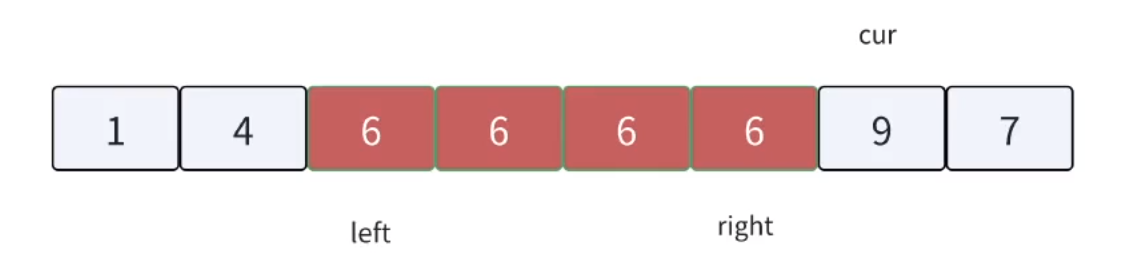
單次循環劃分完畢之后,只需對左右兩塊區間遞歸即可。
void QuickSort(int* arr, int left, int right)
{if(left >= right){return;}int begin = left; int end = right;int key = arr[left];int cur = left + 1;while(cur <= right){if(arr[cur] < key){Swap(&arr[cur], &arr[left]);cur++;left++;}else if(arr[cur] > key){Swap(&arr[cur], &arr[right]);right--;}else{cur++;}}//[begin, left-1] [left, right] [right+1, end]QuickSort(arr, begin, left - 1);QuickSort(arr, right + 1, end);
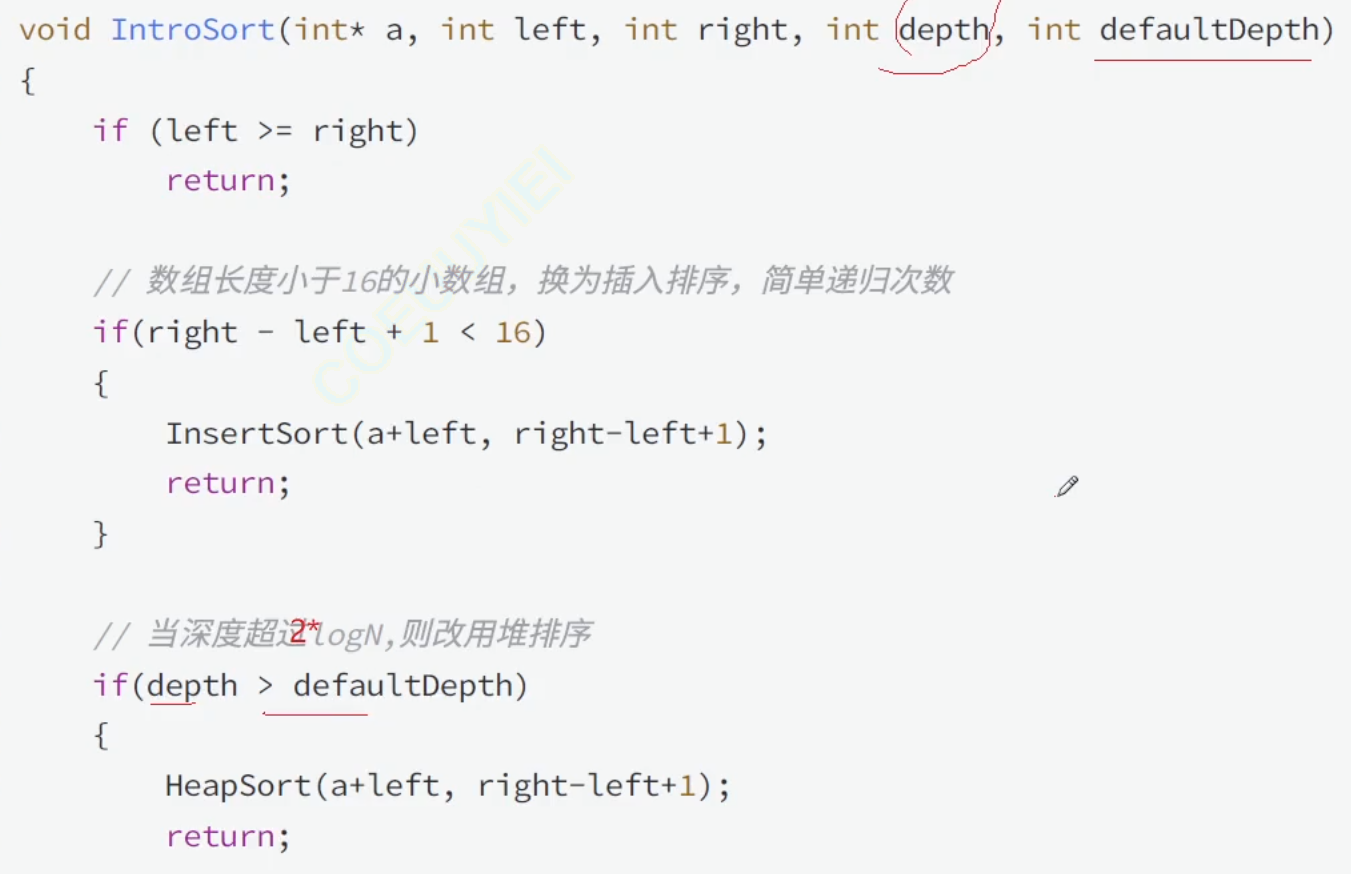
}2、自省排序(introsort)
introsort是introspective sort的縮寫,顧名思義,該方法的思路就是進行自我的偵測與反省,快排遞歸深度太深(sgi STL中使用的是深度為2倍排序元素數量的對數值)那就說明在這種數據序列下,選key出現了問題,性能在快速退化,那么就不要再進行快排分割遞歸了,改換為堆排序進行排序。
了解即可,不做代碼要求。
四、歸并排序 拓展
1、非遞歸版本歸并排序
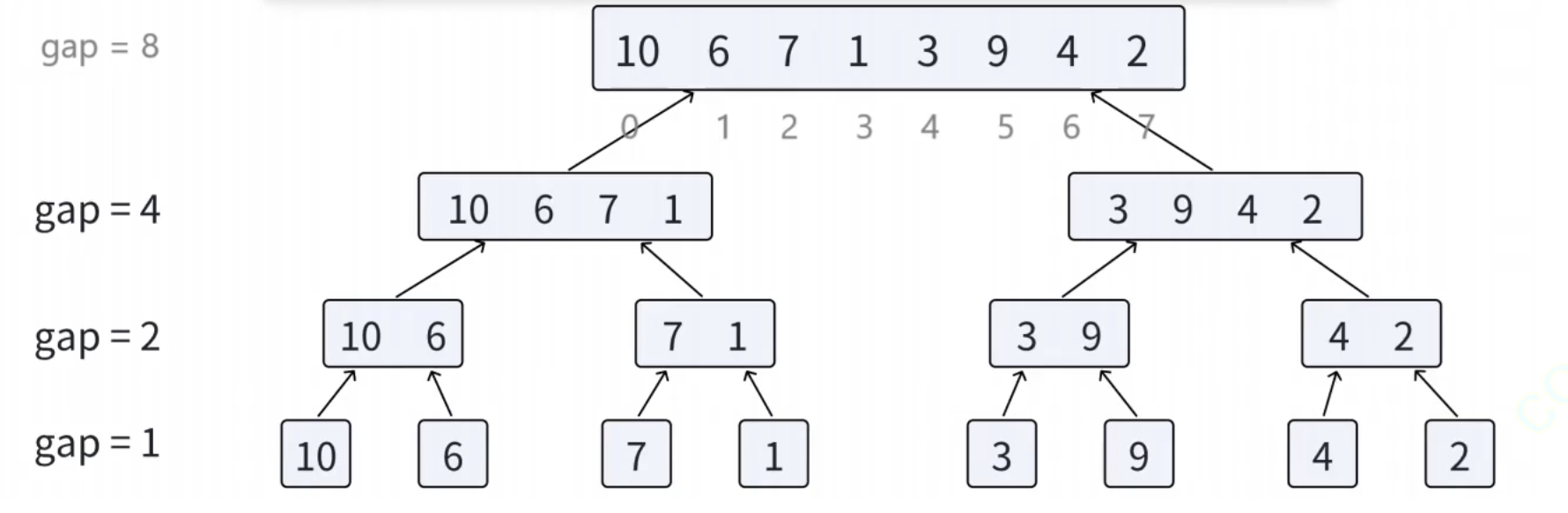
//非遞歸版本歸并排序
void MergeSortNonR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");exit(1);}int gap = 1;while (gap < n){//根據gap劃分組,兩兩一合并for (int i = 0;i < n;i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap + gap - 1;if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}int index = begin1;//兩個有序序列進行合并while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//導入到原數組中memcpy(arr + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}
}2、文件歸并排序
2.1 外排序
外排序(External sorting)是指能夠處理極大量數據的排序算法。通常來說,外排序處理的數據不能能一次裝入內存,只能放在讀寫較慢的外存儲器(通常是硬盤)上。外排序通常采用的是一種“排序---歸并”的策略。在排序階段,先讀入能放在內存中的數據量,將其排序輸出到一個臨時文件,依次進行,將待排序數據組織為多個有序的臨時文件。然后在歸并階段將這些臨時文件組合為一個大的有序文件,即排序結果。
跟外排序對應的就是內排序,我們之間講的常見的排序都是內排序。它們的排序思想適應的是數據在內存中,支持隨機訪問。歸并排序的思想是不需要隨機訪問數據,只需要依次按序列讀取數據,所以歸并排序既是一個內排序,也是一個外排序。
2.2 思路分析

2.3 參考代碼
#include <stdio.h>
#include <stdlib.h>
#include <time.h>//創建N個隨機數,寫到文件中
void CreateNData()
{//造數據int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if(fin == NULL){perror("fopen fail");return;}for(int i = 0;i < n;i++){int x = rand() + i;fprintf(fin, "%d\n", x);}fclose(fin);
}int compare(const void* a, const void* b)
{return (*(int*)a - *(int*)b);
}//返回實際讀到的數據個數,沒有數據就返回0
int ReadNDataSortToFile(FILE* fout, int n, const char* file1)
{FILE* fin = fopen(file1, "w");if(fin == NULL){perror("fopen fail");return -1;}int x = 0;int* arr = (int*)malloc(sizeof(int) * n);if(arr == NULL){perror("malloc fail");return -1;}//讀取n個數據,如果遇到文件結束,應該讀j個int j = 0;for(int i = 0;i < n;i++){if(fscanf(fout, "%d", &x) == EOF){break;}arr[j++] = x;}if(j == 0){return 0;}//排序qsort(arr, j, sizeof(int), compare);//寫回file1文件for(int i = 0;i < j;i++){fprintf(fin, "%d\n", arr[i]);}fclose(fin);return j;
}void MergeFile(const char* file1, const char* file2, const char* mfile)
{FILE* fout1 = fopen(file1, "r");if(fout1 == NULL){perror("fopen fail");return;}FILE* fout2 = fopen(file2, "r");if(fout2 == NULL){perror("fopen fail");return;}FILE* mfin = fopen(mfile, "r");if(mfin == NULL){perror("fopen fail");return;}int x1 = 0;int x2 = 0;int ret1 = fscanf(fout1, "%d", &x1);int ret2 = fscanf(fout2, "%d", &x2);while(ret1 != EOF && ret2 != EOF){if(x1 < x2){fprintf(mfin, "%d\n", x1);ret1 = fscanf(fout1, "%d", &x1);}else{fprintf(mfin, "%d\n", x2);ret2 = fscanf(fout2, "%d", &x2);}}while(ret1 != EOF){fprintf(mfin, "%d\n", x1);ret1 = fscanf(fout1, "%d", &x1);}while(ret2 != EOF){fprintf(mfin, "%d\n", x2);ret2 = fscanf(fout2, "%d", &x2);}
}int main()
{CreateNData();const char* file1 = "file1.txt";const char* file2 = "file2.txt";const char* mfile = "mfile.txt";FILE* fout = fopen("data.txt", "r");if(fout == NULL){perror("fopen fail");return;}ReadNDataSortToFile(fout, 100, file1);ReadNDataSortToFile(fout, 100, file2);while(1){MergeFile(file1, file2, mfile);//刪除file1和file2remove(file1);remove(file2);//重命名mfile為file1rename(mfile, file1);//當再次讀取數據,一個都讀不到,說明已經沒有數據了//已經歸并完成,歸并結果在file1if(ReadNDataSortToFile(fout, 100, file2) == 0){break;}}return 0;
}
)







)


實現底層)






