一、選擇題
(1)
考點:低階無窮小定義、高階無窮小定義、同階無窮小定義、等階無窮小定義、移項變形/極限存在并且分母→0時則分子也→0
方法一:
方法二:
(2)
考點:說不清楚的思路/湊導數定義式、洛必達法則、隱函數求導
方法一:我的方法
方法二:湊導數定義式
(3)
考點:★第一步最重要的是求出分段函數的分段表達式、洛必達法則、連續定義、導數定義
或利用結論:
(4)
考點:p積分、q積分、無窮積分計算
(5)
考點:復合函數求導法則
(6)
考點:二重積分的結果正負只取決于被積函數的正負、普通對稱性、輪換對稱性
(7)
考點:矩陣等價?矩陣的秩相等、一個矩陣乘以一個可逆矩陣其秩不變、右乘操作列
(8)
考點:矩陣可相似對角化的充要條件是有?n 個線性無關的特征向量(即對應特征值的幾何重數等于相應的代數重數)/?實對稱矩陣相似的充分必要條件(兩實對稱矩陣相似?特征多項式相同?特征值全部相同)
方法一:兩實對稱矩陣相似?特征值全部相同
方法二:矩陣可相似對角化的充要條件
方法三:兩實對稱矩陣相似?特征多項式相同
二、填空題
(9)
考點:a^b=e^blna、ln(1+x)的麥克勞林展開
(10)
考點:反函數求導法則、?思路、積分結果為0的兩種情況(上限=下限、被積函數恒等于0)
(11)
考點:計算極坐標系下的平面圖形面積的積分公、(不是計算極坐標弧長積分)
(12)
考點:法線的定義、參數方程求導
(13)
考點:非齊次特解的差是齊次的解、若有兩個解是齊次的解且線性無關則C1解1+C2解2就是齊次的通解(P332)、解1/解2=函數≠常數則兩個解線性無關
★新題型(14)
考點:|A|=|A^T|、|AA*|=|A|^n、伴隨矩陣定義、拉普拉斯展開
同類型題目
三、解答題
(15)
考點:cosx的麥克勞林展開、等價無窮小的定義
(16)
考點:圓盤法、柱殼法
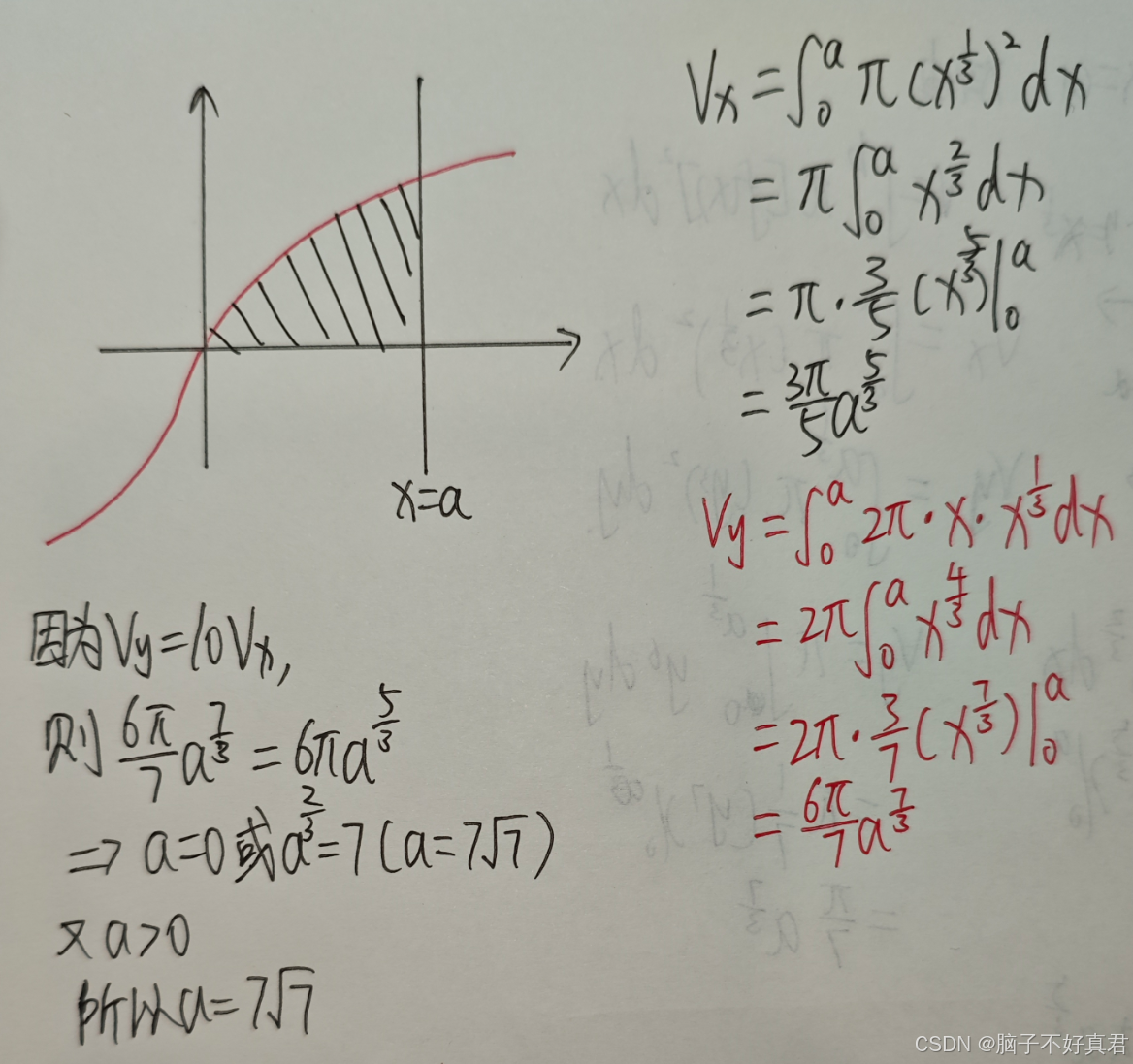
方法一:一個圓盤法+一個柱殼法
方法二:兩個圓盤法
(17)
考點:計算量
方法一:直角坐標
方法二:極坐標
(18)
考點:奇函數f(x), f(0)=0、奇函數求導是偶函數、偶函數f(x)=f(-x)、注意運動第一問得到的結論、拉格朗日中值定理、羅爾定理、設輔助函數
(Ⅰ)
方法一:拉格朗日中值定理
方法二:輔助函數+羅爾定理
(Ⅱ)
方法一:輔助函數_1+羅爾定理
方法二:輔助函數_2+羅爾定理
★(19)
考點:拉格朗日乘數法、坐標系點與點的距離公式
(20)
考點:n→∞的條件是在計算極限的時候才使用、取極限"<"變等號"<="
(Ⅰ)
(Ⅱ)
(21)
考點:直角坐標系弧長積分公式、平面圖形面積積分公式、形心積分公式、描點法判斷積分區域
(Ⅰ)
(Ⅱ)
(22)
考點:看下列方法
方法一:轉化為增廣矩陣解線性方程組
方法二(不推薦):硬解方程組、如果方程組有解且未知數個數 > 方程個數, 則方程組有無窮多解
(23)
考點:
二次型對應矩陣的定義(一個二次型對應著一個對稱矩陣.若 A?是一個實對稱矩陣,且f=x^T?A x,則稱 A 為二次型 f 對應的對稱矩陣)、
二次型正交變換后的對角矩陣系數就是二次型對稱矩陣的特征值、
當?α 是一個單位向量時, 模長為1即 ∣∣α∣∣=1, α^T α=1、
對任何非零 n 維列向量 α,β,矩陣 βa^T的秩均為1(在1000上證過)、
若 A 不滿秩, 則 0 也是 A 的一個特征值、
矩陣秩的次加性:兩個矩陣和的秩,小于或等于它們各自秩的和
(Ⅰ)
方法一:用向量表示二次型
方法二(不推薦):硬展
(Ⅱ)



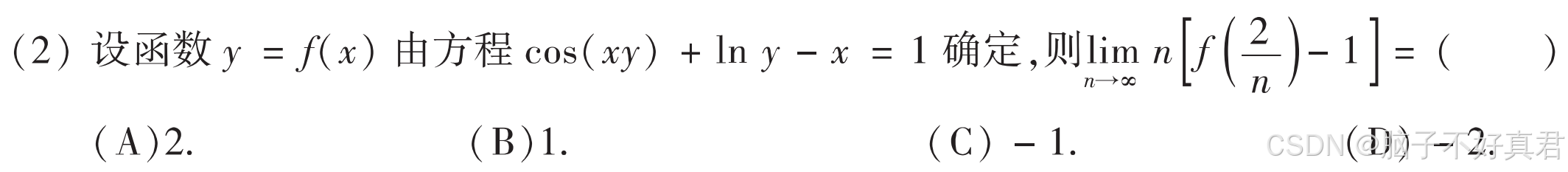
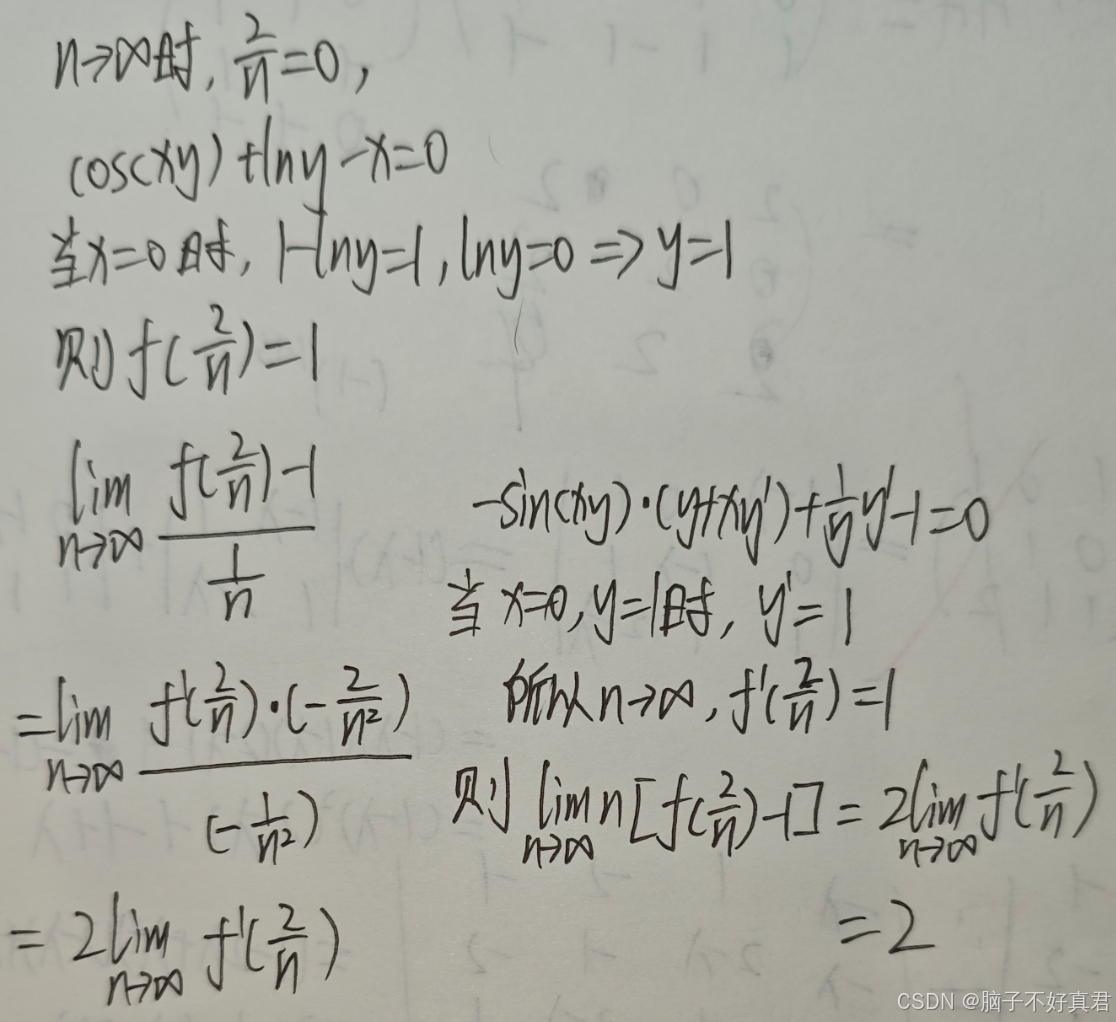






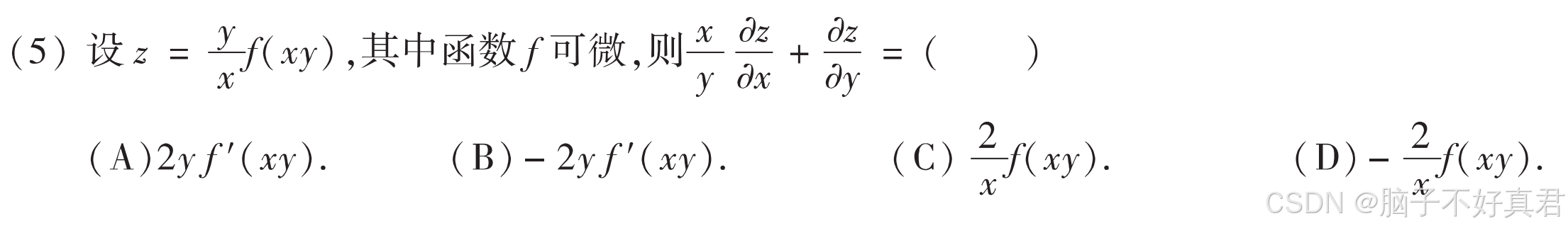









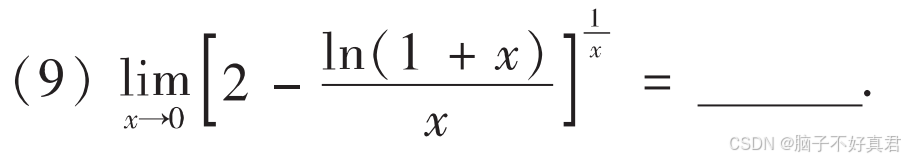
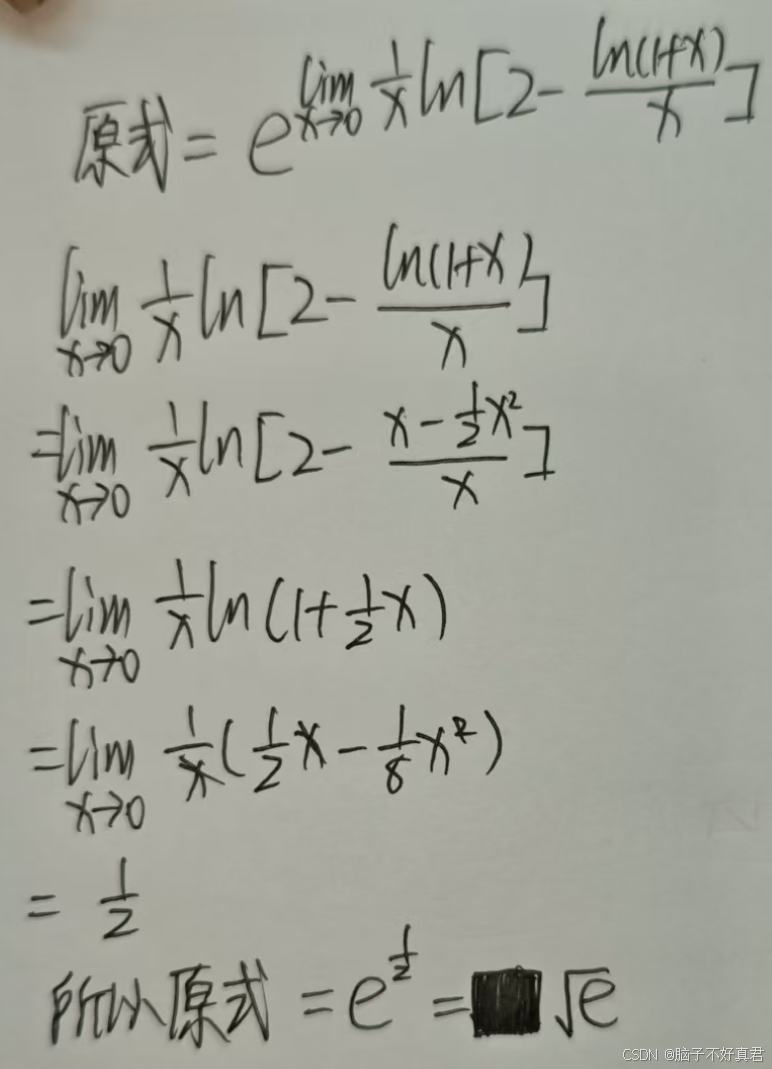




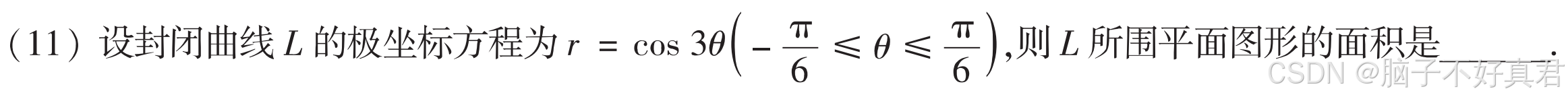

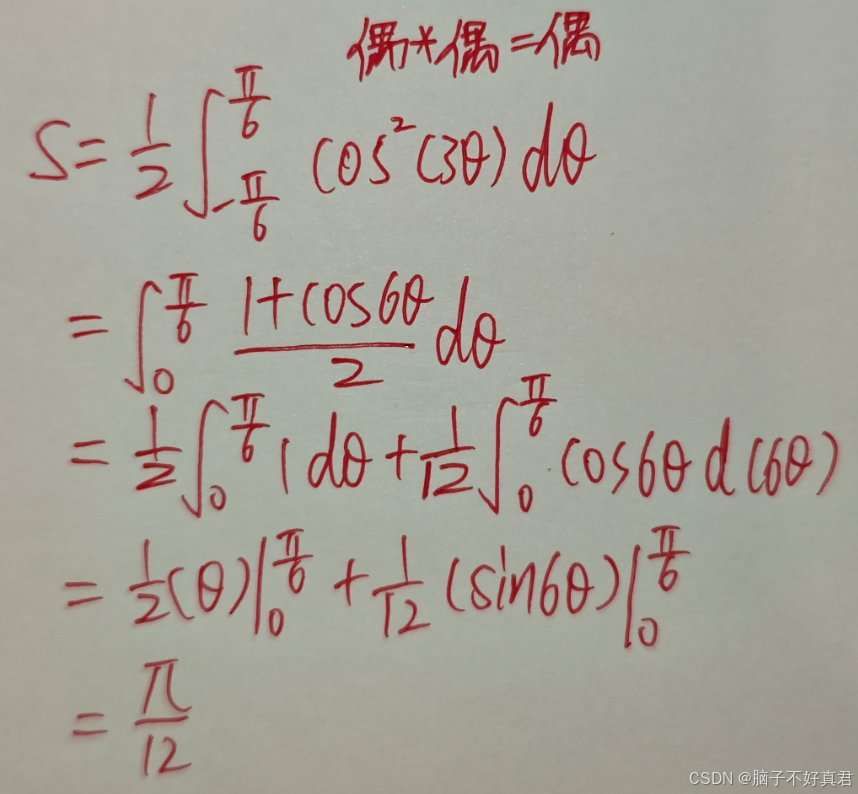
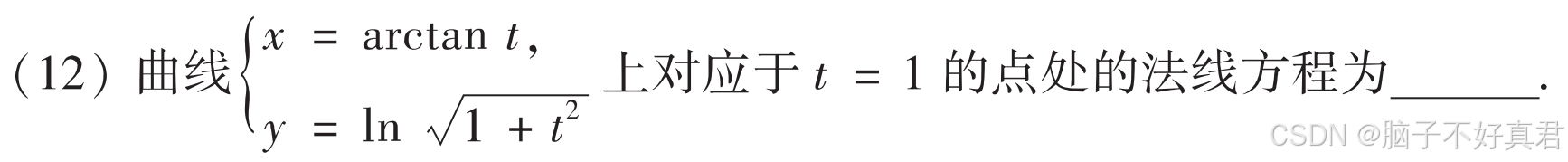
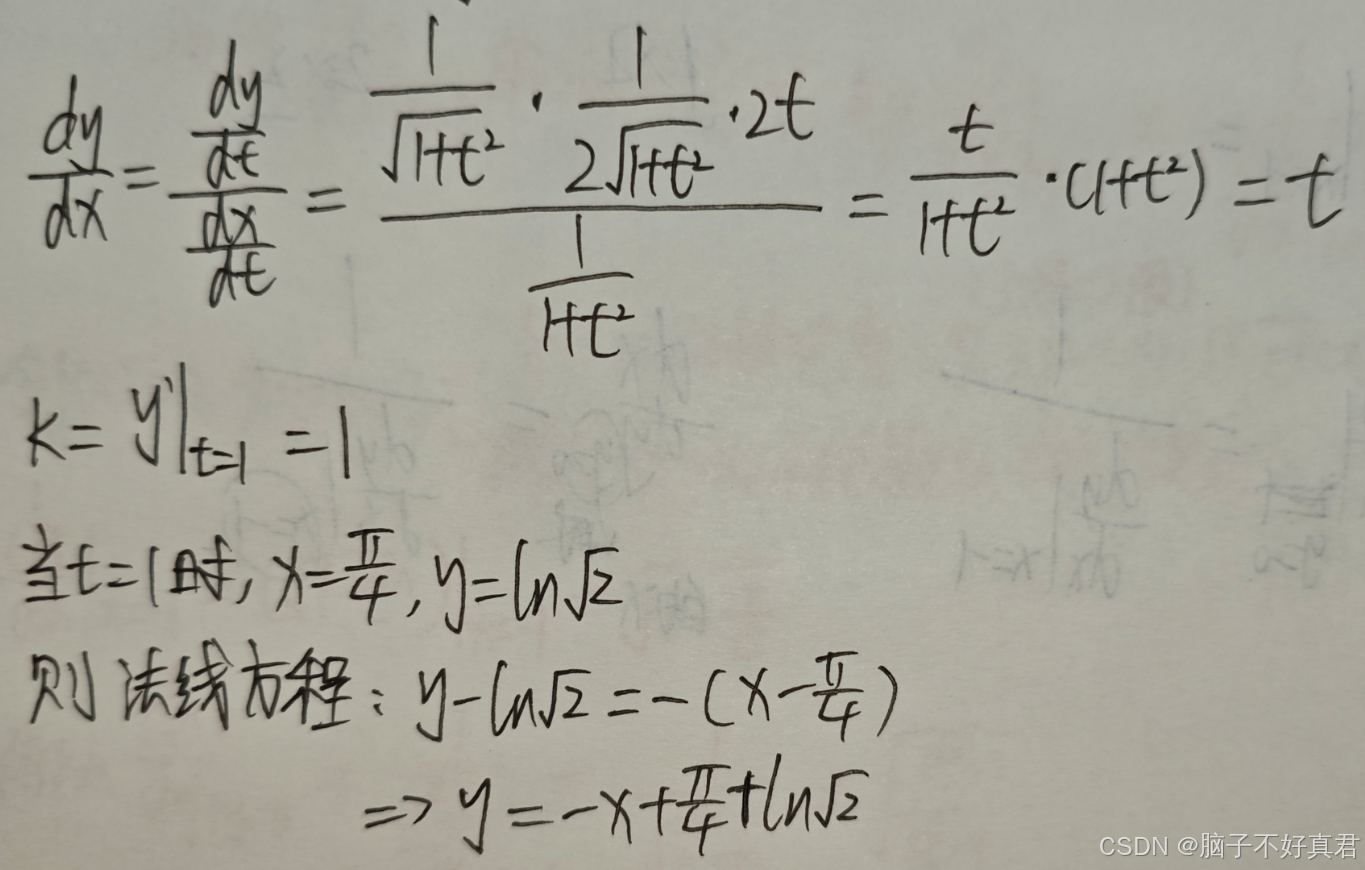



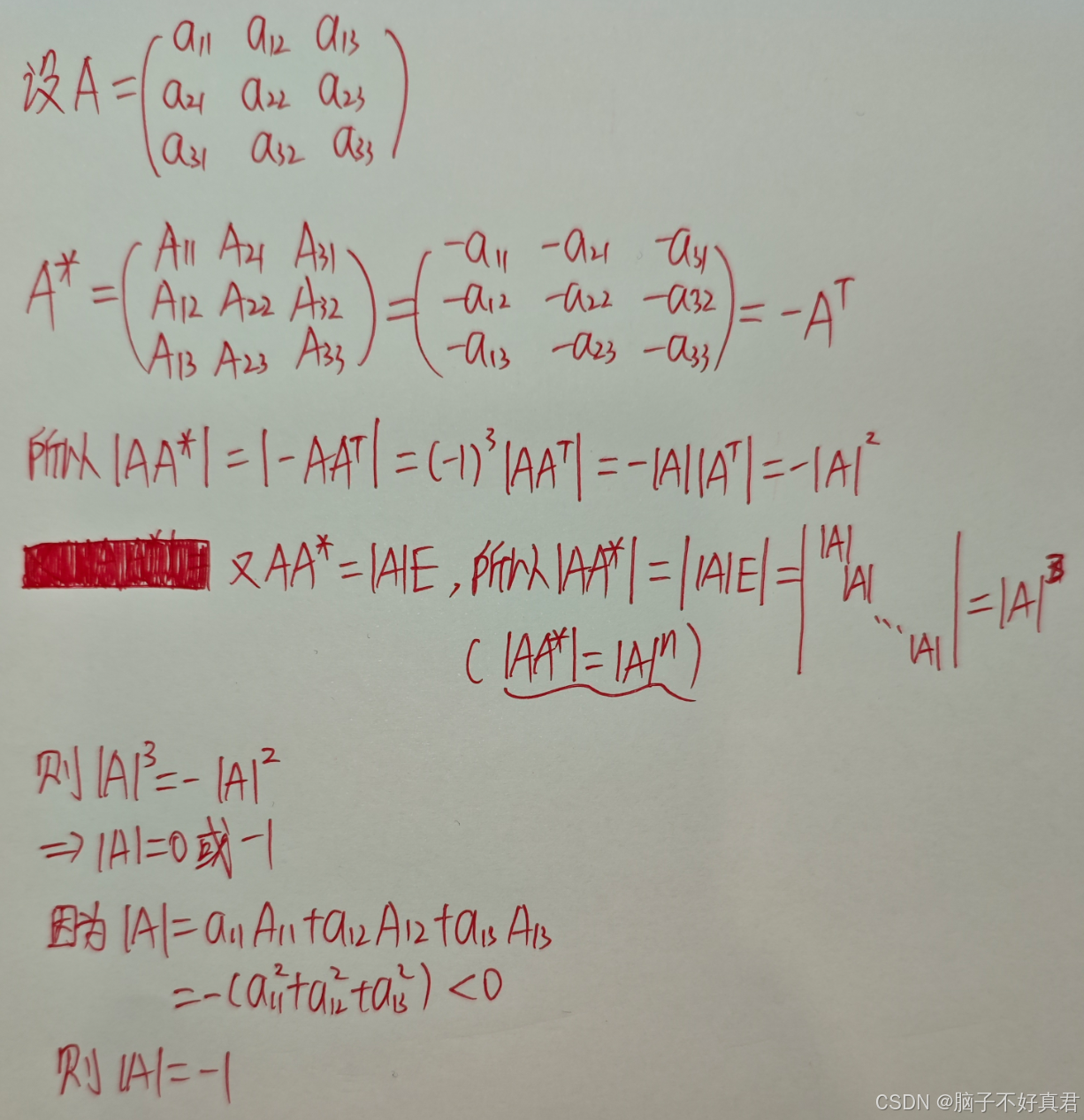

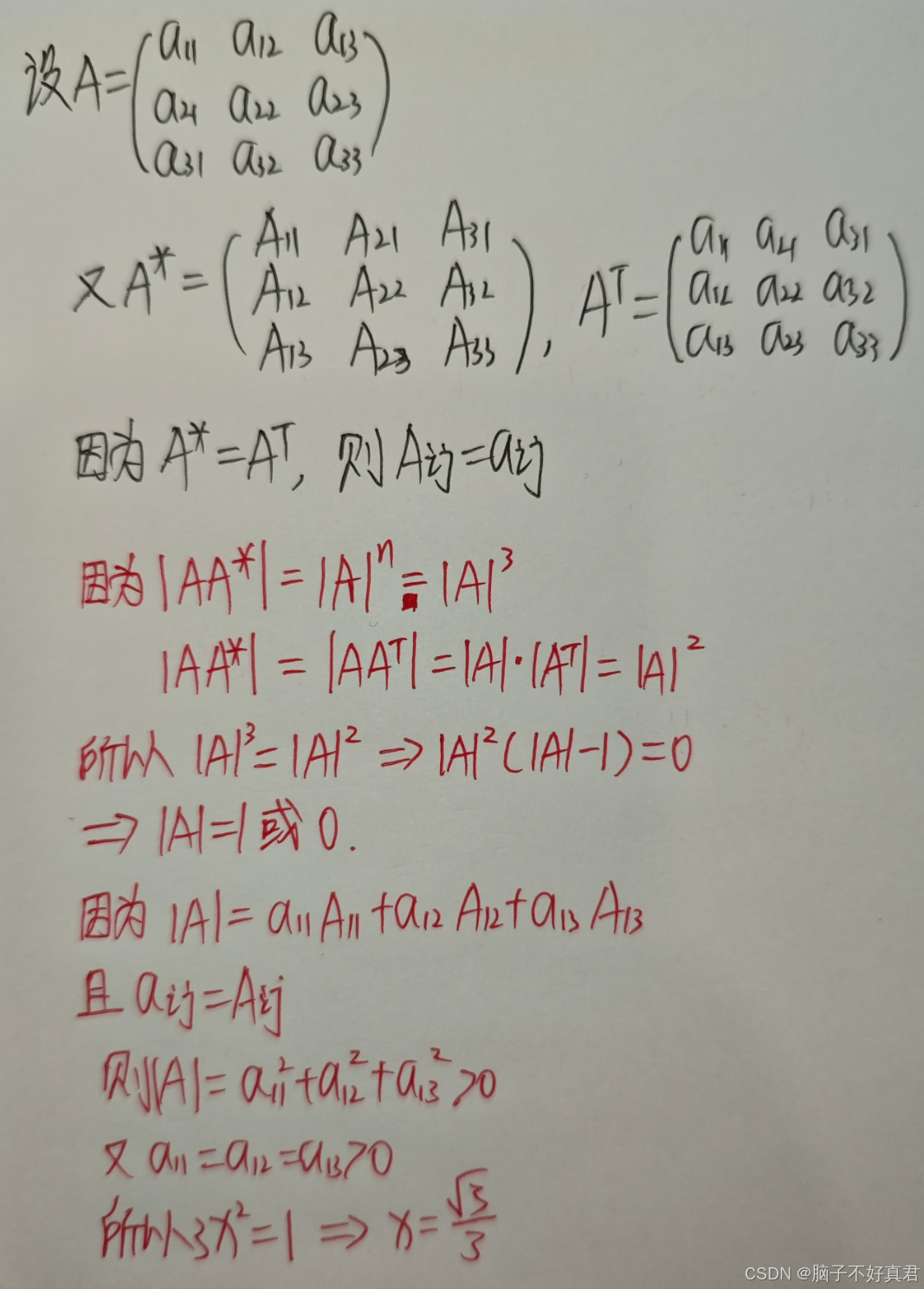
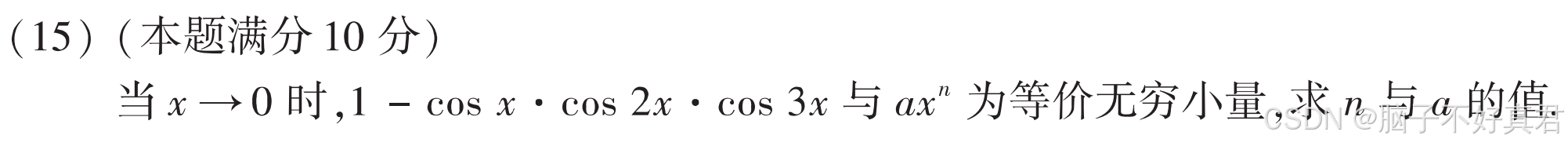
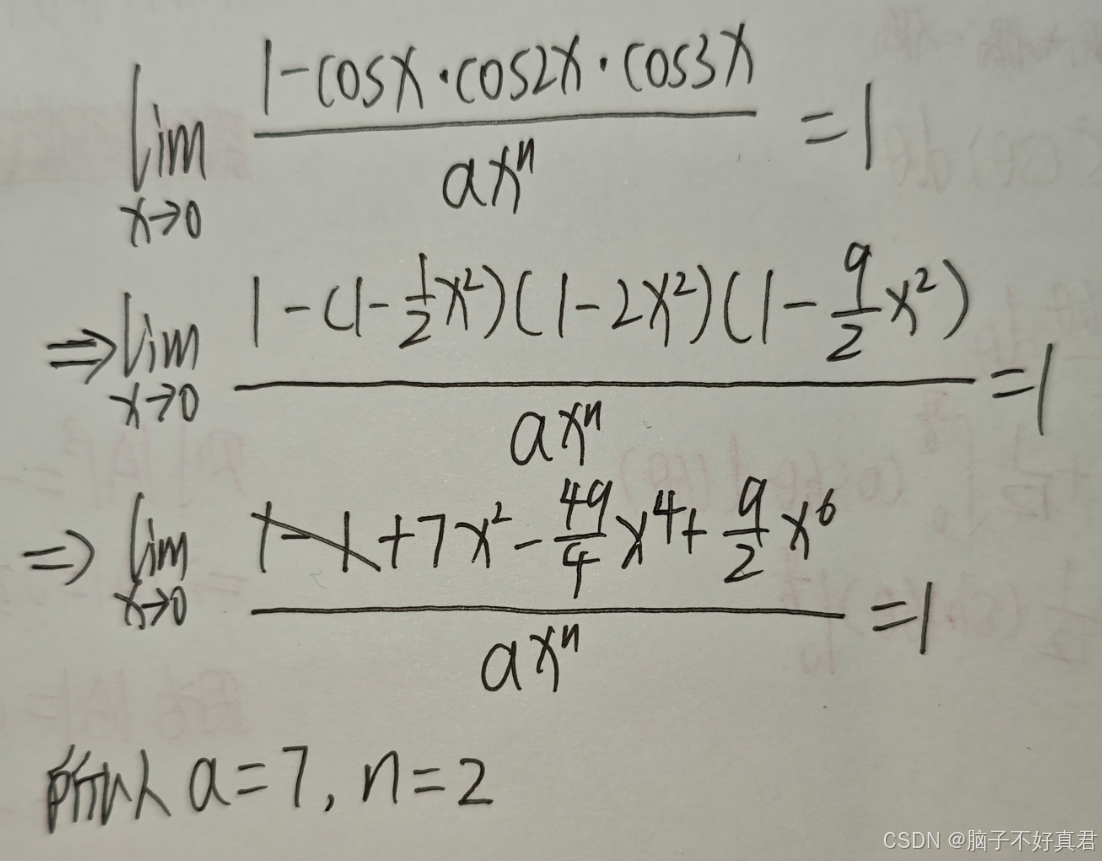
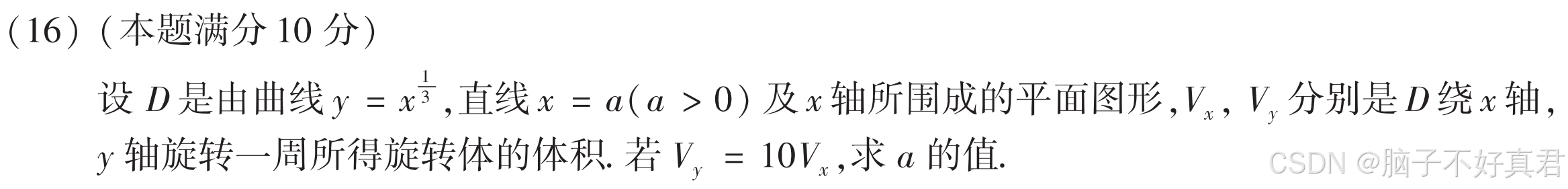
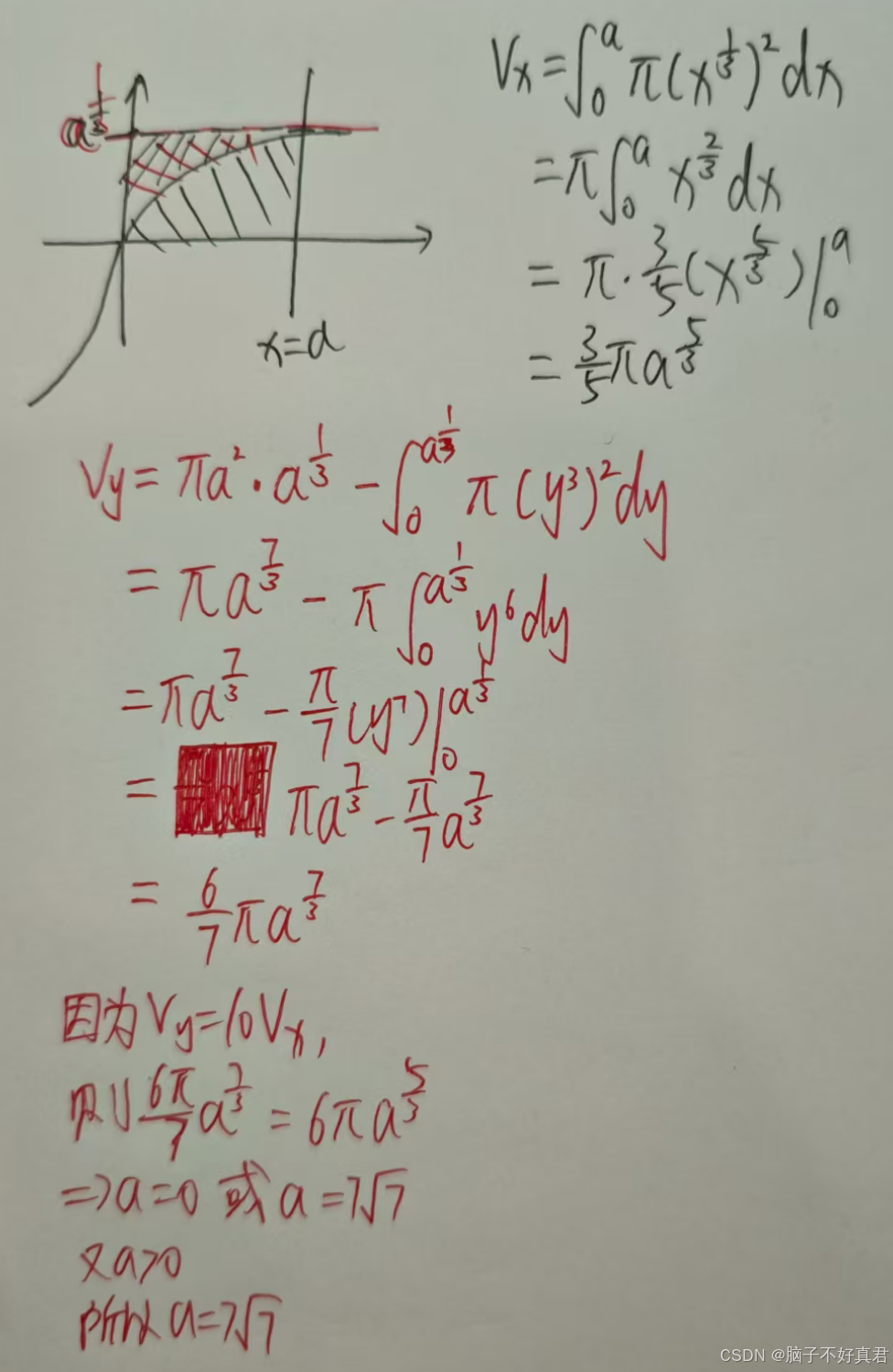
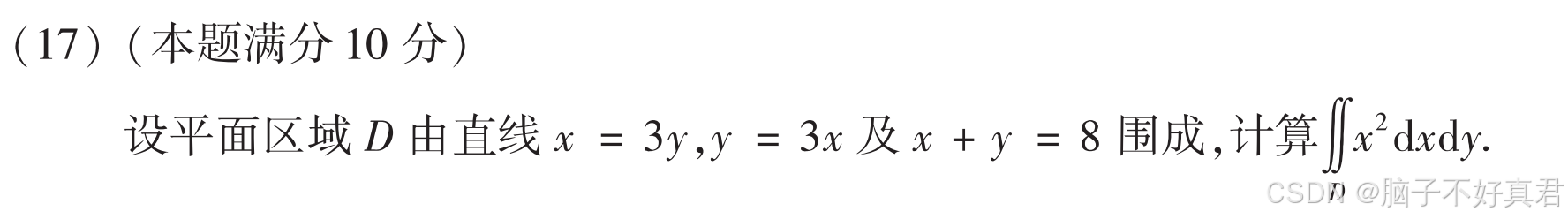
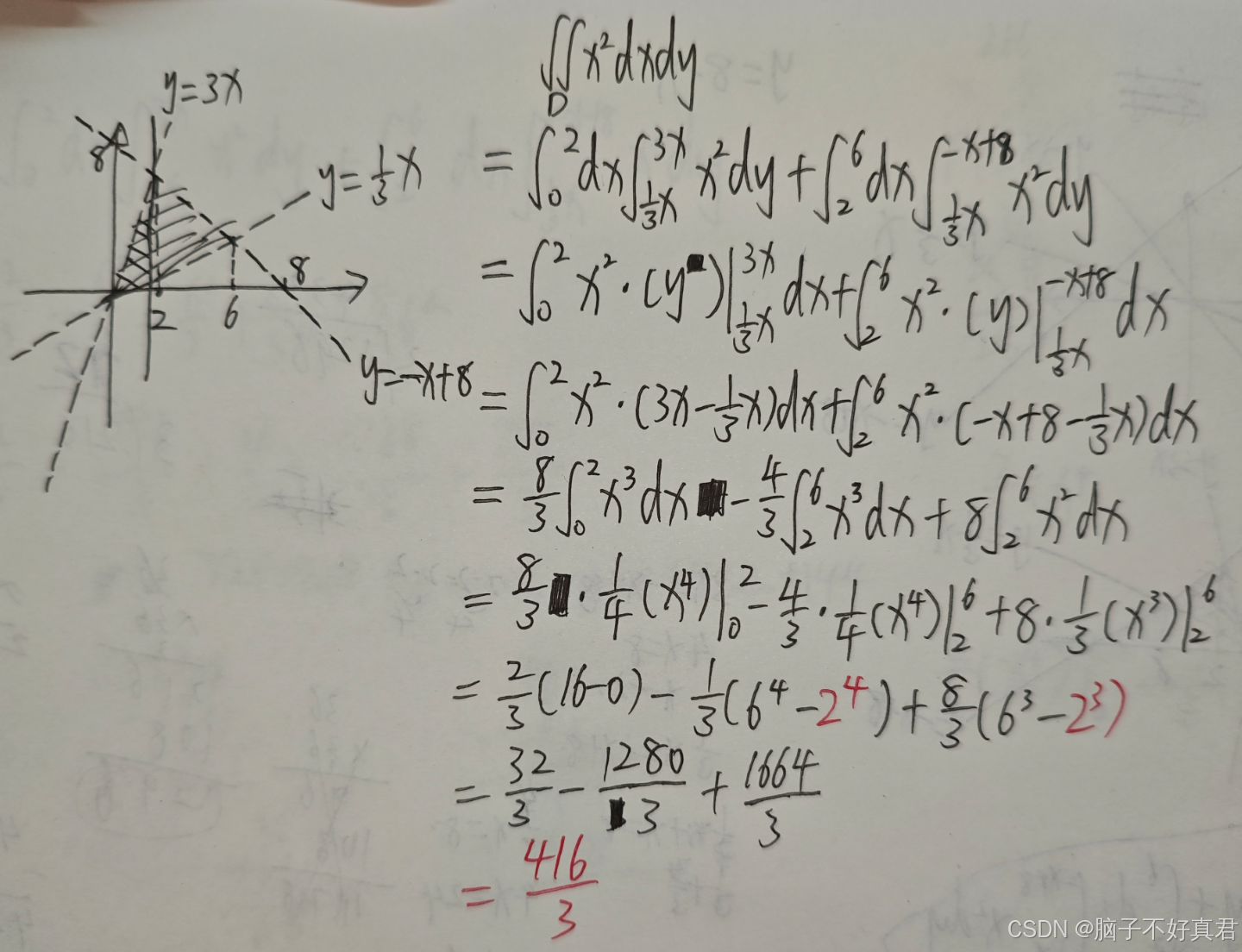
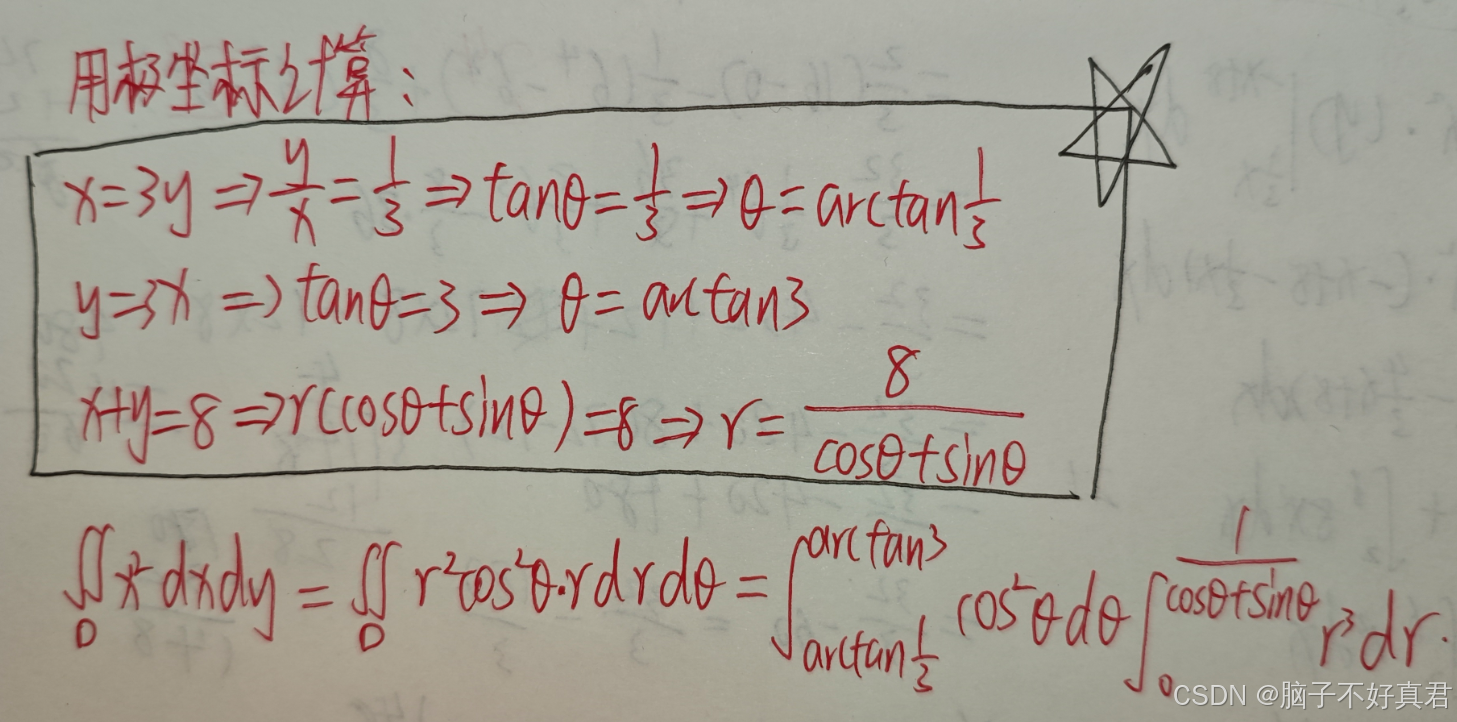
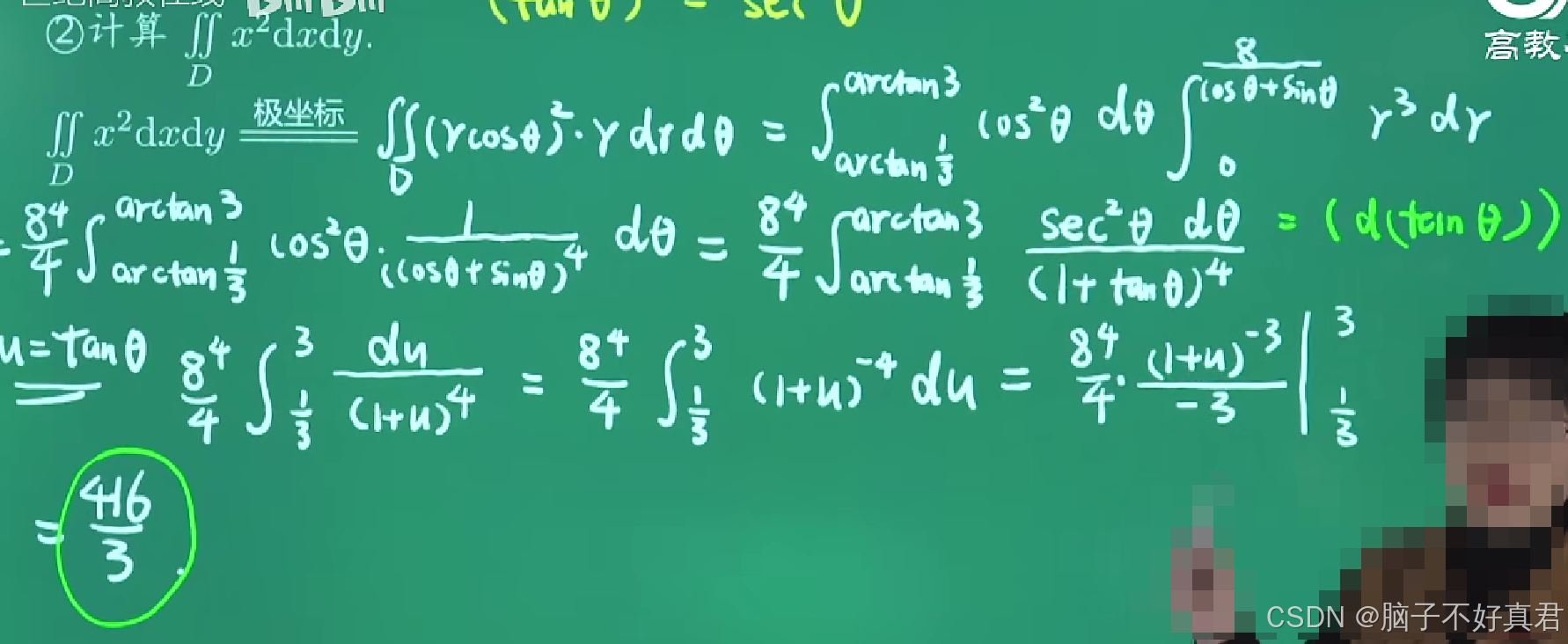





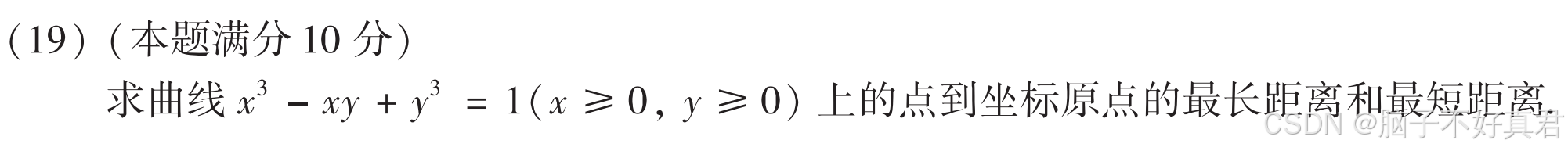

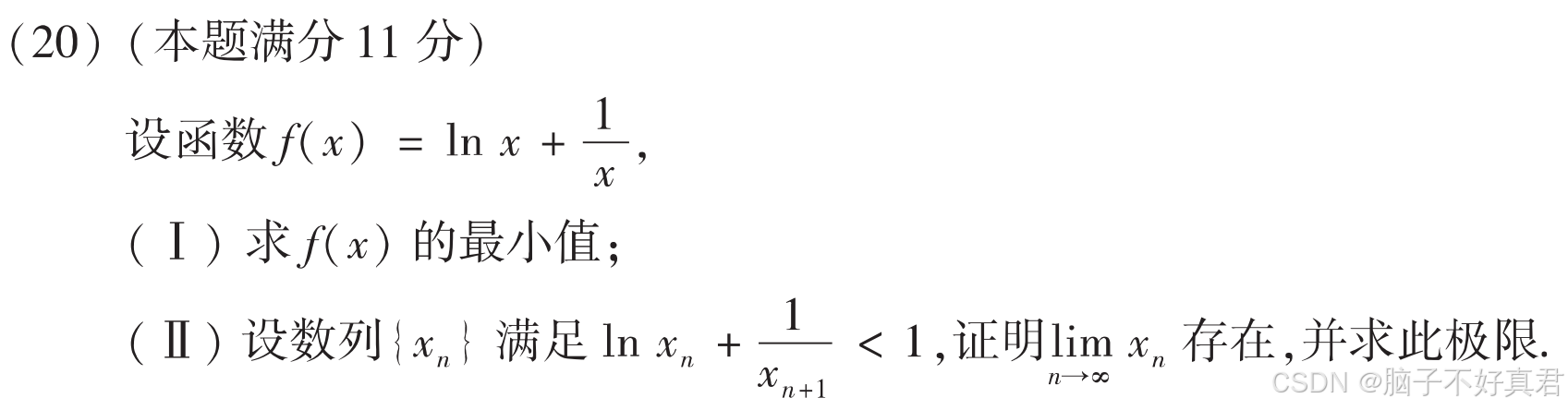


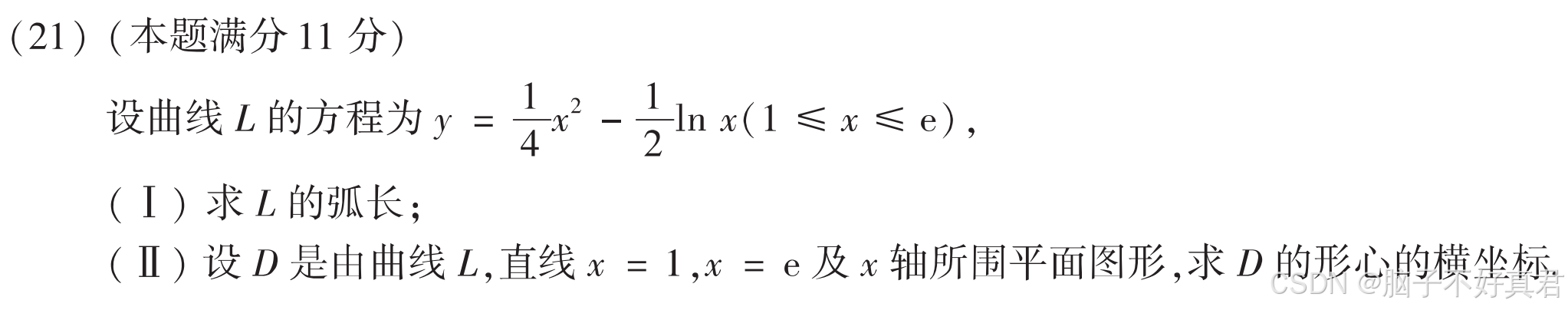

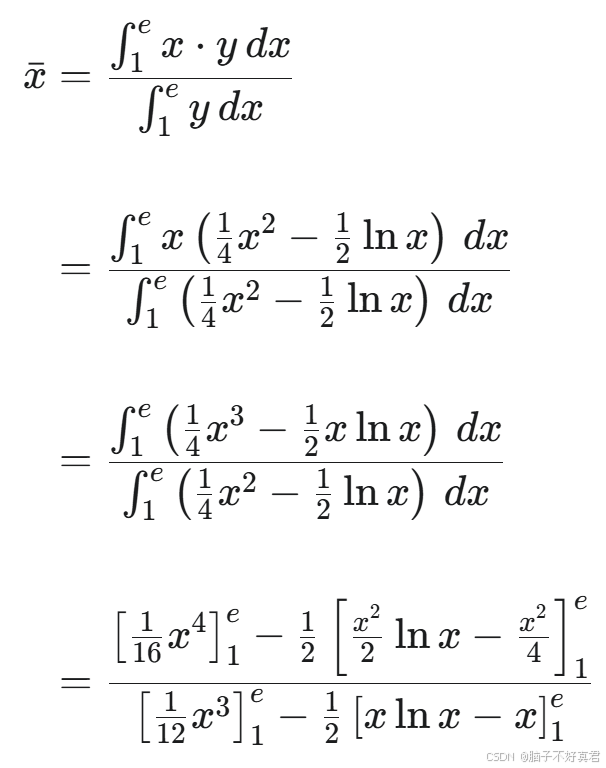

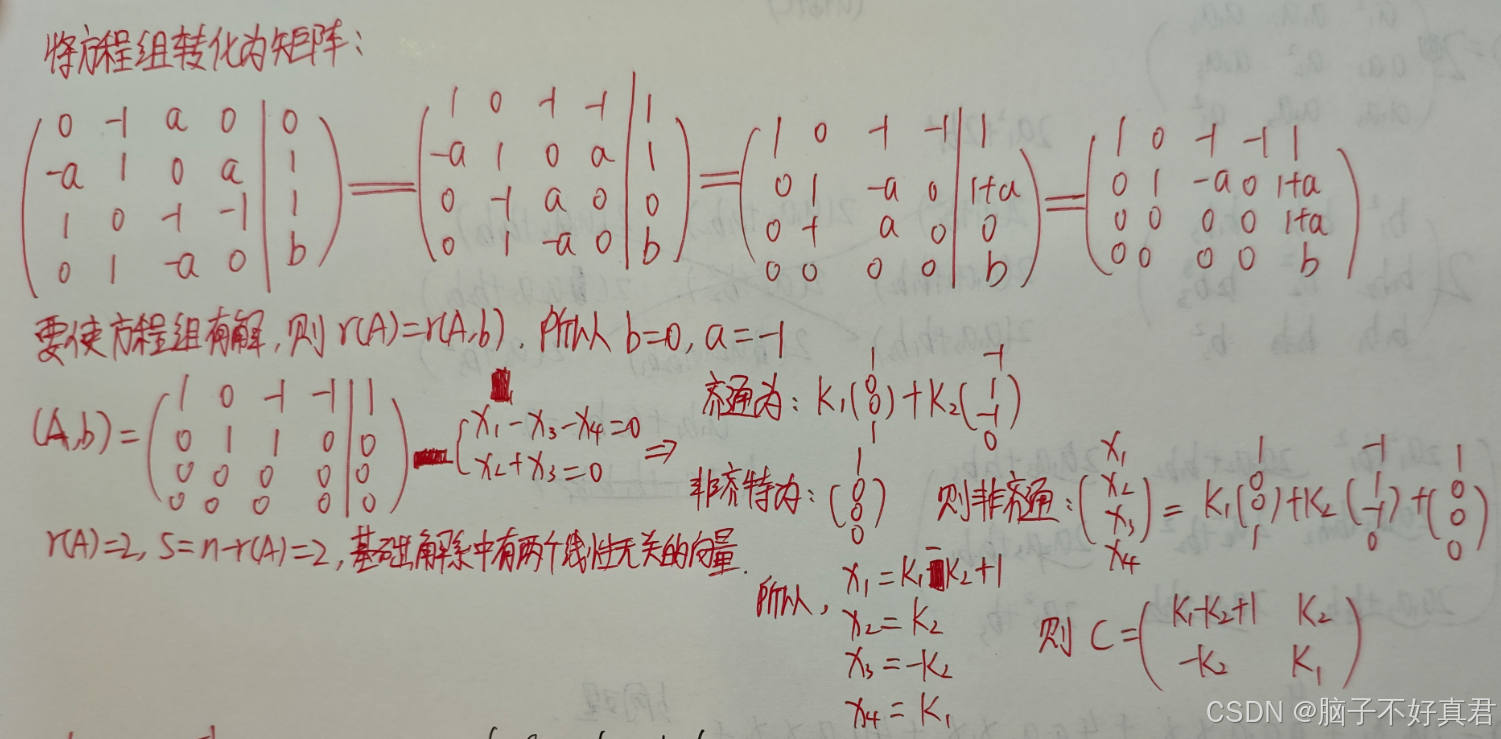





:創建與使用指南)
_學習筆記)







詳細講解Linux調試器 gdb/cgdb使用)


)

)




