【深度學習②】| DNN篇

0 序言

本文將系統介紹基于PyTorch的深度神經網絡（DNN）相關知識，包括張量的基礎操作、DNN的工作原理、實現流程，以及批量梯度下降、小批量梯度下降方法和手寫數字識別案例。通過學習，你將掌握DNN的核心概念、PyTorch實操技能，理解從數據處理到模型訓練、測試的完整流程，具備搭建和應用簡單DNN模型的能力。

1 張量

在深度學習中，數據的表示與處理是所有操作的基礎。張量作為PyTorch中最核心的數據結構，承載著數據存儲與計算的功能，是構建神經網絡、實現模型訓練的前提。因此，我們首先從張量的基本概念和操作入手。

1.1 數組與張量

NumPy的數組和PyTorch的張量是數據處理的核心結構，二者在語法上高度相似，但張量支持GPU加速，更適用于深度學習。因此在學習本小節前，如果你沒有NumPy數組的相關基礎，點此鏈接先學習后再學習本文：深度學習①-NumPy數組篇

對應關系：np對應torch，數組array對應張量tensor，n維數組對應n階張量。
轉換方法：
1.數組轉張量：ts = torch.tensor(arr)
2.張量轉數組：arr = np.array(ts)

1.2 從數組到張量

PyTorch在NumPy基礎上修改了部分函數或方法，主要差異見下表：

NumPy的函數	PyTorch的函數	用法區別
`.astype()`	`.type()`	無
`np.random.random()`	`torch.rand()`	無
`np.random.randint()`	`torch.randint()`	不接納一維張量
`np.random.normal()`	`torch.normal()`	不接納一維張量
`np.random.randn()`	`torch.randn()`	無
`.copy()`	`.clone()`	無
`np.concatenate()`	`torch.cat()`	無
`np.split()`	`torch.split()`	參數含義優化
`np.dot()`	`torch.matmul()`	無
`np.dot(v,v)`	`torch.dot()`	無
`np.dot(m,v)`	`torch.mv()`	無
`np.dot(m,m)`	`torch.mm()`	無
`np.exp()`	`torch.exp()`	必須傳入張量
`np.log()`	`torch.log()`	必須傳入張量
`np.mean()`	`torch.mean()`	必須傳入浮點型張量
`np.std()`	`torch.std()`	必須傳入浮點型張量

1.3 用GPU存儲張量

默認情況下，張量存儲在CPU中，而GPU能顯著提升計算速度，因此需掌握張量和模型的GPU遷移方法。

張量遷移到GPU：

import torch
ts1 = torch.randn(3,4)  # 存儲在CPU
ts2 = ts1.to('cuda:0')  # 遷移到第一塊GPU（cuda:0）

模型遷移到GPU：

class DNN(torch.nn.Module):  # 定義神經網絡類pass  # 具體結構略
model = DNN().to('cuda:0')  # 模型遷移到GPU

查看GPU運行情況：在cmd中輸入nvidia-smi，可查看顯卡型號、內存使用等信息。當然了，硬件設備沒有GPU的直接用CPU也行，速度慢一些，如果你電腦里有多個顯卡，那你可以遷移到多塊上，比如會有cuda：1、cuda：2等等。

2 DNN的原理

上一章介紹了數據的基礎載體，也就是張量，而深度神經網絡的核心是通過學習數據特征擬合輸入與輸出的關系。本章將解析DNN的工作原理，包括數據集處理、訓練、測試和使用的完整流程。

2.1 劃分數據集

數據集是模型學習的基礎，需包含輸入特征和輸出特征，并劃分為訓練集（用于模型學習）和測試集（用于驗證模型泛化能力）。

劃分原則：通常按7:3或8:2的比例劃分，如1000個樣本中800個為訓練集，200個為測試集。
對應關系：輸入特征的數量決定輸入層神經元數，輸出特征的數量決定輸出層神經元數（例如：3個輸入特征→輸入層3個神經元，3個輸出特征→輸出層3個神經元）。

2.2 訓練網絡

訓練是DNN優化內部參數（權重和偏置）的過程，通過前向傳播計算預測值，再通過反向傳播調整參數，最終擬合函數。

2.2.1 前向傳播

輸入特征從輸入層逐層傳遞到輸出層，每個神經元的計算為：

線性計算： $\omega_1 x_1 + \omega_2 x_2 + ... + \omega_n x_n + b$
其中， $ω\omega$ 為權重， $b$ 為偏置
非線性轉換： $\sigma(\text{線性計算結果})$
其中， $σ\sigma$ 為激活函數，如ReLU、Sigmoid，用于引入非線性，避免多層網絡等效于單層）

2.2.2 反向傳播

通過損失函數計算預測值與真實值的差距，再反向求解梯度，調整權重和偏置以減小損失。

損失函數：衡量預測誤差（如MSE、BCELoss）。
學習率：控制參數調整幅度，過大可能導致損失震蕩，過小則收斂緩慢。

2.2.3 batch_size

每次前向傳播和反向傳播的樣本數量，影響訓練效率和穩定性：

批量梯度下降（BGD）：一次輸入所有樣本，計算量大、速度慢。
隨機梯度下降（SGD）：一次輸入1個樣本，速度快但收斂不穩定。
小批量梯度下降（MBGD）：一次輸入若干樣本（如32、64），平衡效率和穩定性，常用且batch_size通常設為2的冪次方。

2.2.4 epochs

全部樣本完成一次前向和反向傳播的次數。例：10240個樣本，batch_size=1024，則1個epoch包含10240/1024=10次傳播，5個epoch共50次傳播。

2.3 測試網絡

測試用于驗證模型的泛化能力，避免過擬合，

過擬合就是模型僅適配訓練集，對新數據無效。

比如說在訓練集準確率能到100%，但是到新數據集只有50-60%這種情況。

解決方法：用測試集輸入進行前向傳播，對比預測輸出與真實輸出，計算準確率。

2.4 使用網絡

訓練好的模型可用于新數據預測，只需輸入新樣本的特征，通過一次前向傳播得到輸出。

3 DNN的實現

掌握了DNN的原理后，本章將通過PyTorch實操實現一個完整的DNN模型，包括數據集制作、網絡搭建、訓練、測試及模型保存。

3.1 制作數據集

需生成包含輸入和輸出特征的樣本，并劃分訓練集和測試集。

import torch# 生成10000個樣本，3個輸入特征（均勻分布），3個輸出特征（One-Hot編碼）
X1 = torch.rand(10000, 1)
X2 = torch.rand(10000, 1)
X3 = torch.rand(10000, 1)
Y1 = ((X1 + X2 + X3) < 1).float()
Y2 = ((1 < (X1 + X2 + X3)) & ((X1 + X2 + X3) < 2)).float()
Y3 = ((X1 + X2 + X3) > 2).float()# 整合數據集并遷移到GPU
Data = torch.cat([X1, X2, X3, Y1, Y2, Y3], axis=1).to('cuda:0')# 劃分訓練集（70%）和測試集（30%）
Data = Data[torch.randperm(Data.size(0)), :]  # 打亂順序
train_size = int(len(Data) * 0.7)
train_Data = Data[:train_size, :]
test_Data = Data[train_size:, :]

3.2 搭建神經網絡

基于torch.nn.Module構建網絡，需定義__init__（網絡結構）和forward（前向傳播）方法。

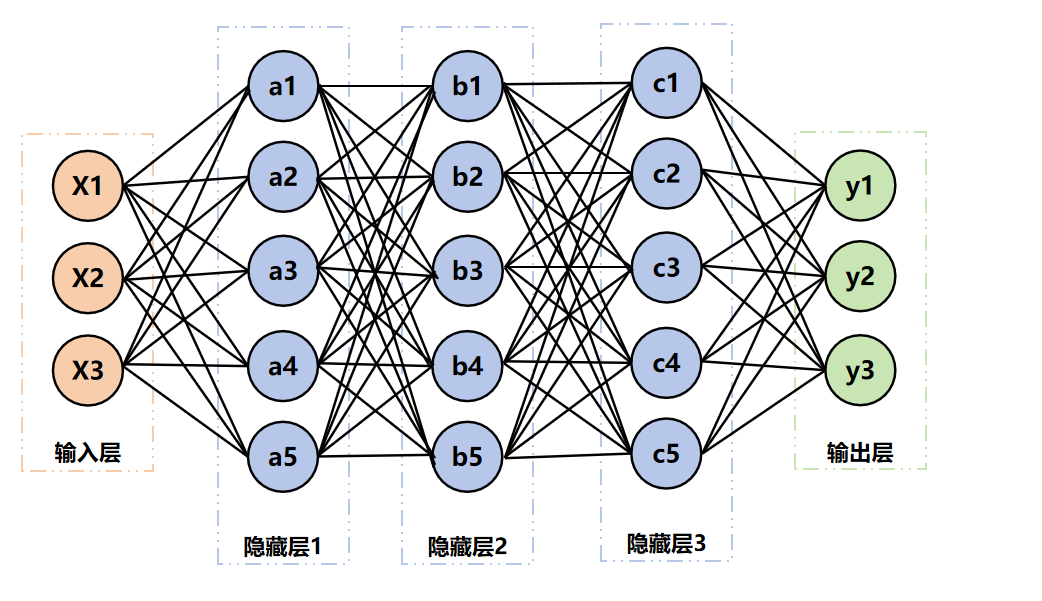
import torch.nn as nnclass DNN(nn.Module):def __init__(self):super(DNN, self).__init__()self.net = nn.Sequential(nn.Linear(3, 5), nn.ReLU(),  # 輸入層→隱藏層1（3→5神經元，ReLU激活）nn.Linear(5, 5), nn.ReLU(),  # 隱藏層1→隱藏層2nn.Linear(5, 5), nn.ReLU(),  # 隱藏層2→隱藏層3nn.Linear(5, 3)  # 隱藏層3→輸出層（5→3神經元）)def forward(self, x):return self.net(x)  # 前向傳播# 創建模型并遷移到GPU
model = DNN().to('cuda:0')

其中，

self.net = nn.Sequential(nn.Linear(3, 5), nn.ReLU(),  # 輸入層→隱藏層1（3→5神經元，ReLU激活）nn.Linear(5, 5), nn.ReLU(),  # 隱藏層1→隱藏層2nn.Linear(5, 5), nn.ReLU(),  # 隱藏層2→隱藏層3nn.Linear(5, 3)  # 隱藏層3→輸出層（5→3神經元）
)

以上程序的計算邏輯如下圖：

在這里插入圖片描述

3.3 網絡的內部參數

內部參數即權重（weight）和偏置（bias），初始為隨機值（如Xavier、He初始值），訓練中不斷優化。

查看參數：

for name, param in model.named_parameters():print(f"參數:{name}\n 形狀:{param.shape}\n 數值:{param}\n")

參數特點：存儲在GPU上（device='cuda:0'），且開啟梯度計算（requires_grad=True）。

3.4 網絡的外部參數

外部參數（超參數）需在訓練前設定，包括：

網絡結構：層數、隱藏層節點數、激活函數（如ReLU、Sigmoid）。
訓練參數：損失函數（如nn.MSELoss()）、優化器（如torch.optim.SGD）、學習率、batch_size、epochs。

3.5 訓練網絡

通過多輪前向傳播、損失計算、反向傳播和參數優化，最小化損失。

epochs = 1000
losses = []  # 記錄損失變化
loss_fn = nn.MSELoss()  # 損失函數
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # 優化器# 提取訓練集輸入和輸出
X = train_Data[:, :3]
Y = train_Data[:, -3:]for epoch in range(epochs):Pred = model(X)  # 前向傳播loss = loss_fn(Pred, Y)  # 計算損失losses.append(loss.item())  # 記錄損失optimizer.zero_grad()  # 清空梯度loss.backward()  # 反向傳播optimizer.step()  # 更新參數

3.6 測試網絡

關閉梯度計算，用測試集驗證模型準確率。

# 提取測試集輸入和輸出
X = test_Data[:, :3]
Y = test_Data[:, -3:]with torch.no_grad():  # 關閉梯度Pred = model(X)  # 前向傳播# 規整預測值（與真實值格式一致）Pred[:, torch.argmax(Pred, axis=1)] = 1Pred[Pred != 1] = 0# 計算準確率correct = torch.sum((Pred == Y).all(1))total = Y.size(0)print(f'測試集精準度: {100 * correct / total} %')

3.7 保存與導入網絡

訓練好的模型需保存，以便后續使用。

保存模型：torch.save(model, 'model.pth')
導入模型：new_model = torch.load('model.pth')
驗證導入：用新模型測試，準確率應與原模型一致。

3.8 完整程序

這里演示的并未用到GPU。

import torch
import torch.nn as nn
import torch.optim as optim# ======================== 1. 制作數據集 ======================== #
# 生成3個輸入特征（均勻分布在[0,1)），共10000個樣本
X1 = torch.rand(10000, 1)  # 輸入特征1
X2 = torch.rand(10000, 1)  # 輸入特征2
X3 = torch.rand(10000, 1)  # 輸入特征3# 計算3個輸出特征（One-Hot編碼，對應和的三個區間）
sum_xy = X1 + X2 + X3
Y1 = (sum_xy < 1).float()          # 和 < 1 → 類別1
Y2 = ((sum_xy >= 1) & (sum_xy < 2)).float()  # 1 ≤ 和 < 2 → 類別2（修正邊界，避免遺漏）
Y3 = (sum_xy >= 2).float()         # 和 ≥ 2 → 類別3# 拼接輸入和輸出特征，形成完整數據集（共6列：3輸入 + 3輸出）
data = torch.cat([X1, X2, X3, Y1, Y2, Y3], dim=1)# 打亂數據順序（避免訓練時樣本順序影響）
shuffled_index = torch.randperm(data.shape[0])  # 生成隨機索引
data = data[shuffled_index]# 劃分訓練集（70%）和測試集（30%）
train_size = int(len(data) * 0.7)
train_data = data[:train_size]
test_data = data[train_size:]# ======================== 2. 搭建神經網絡 ======================== #
class DNN(nn.Module):def __init__(self):super(DNN, self).__init__()# 構建網絡：3層隱藏層，每層5個神經元，ReLU激活self.net = nn.Sequential(nn.Linear(3, 5),  # 輸入層（3特征）→ 隱藏層1（5神經元）nn.ReLU(),        # 激活函數：引入非線性，避免網絡退化為線性模型nn.Linear(5, 5),  # 隱藏層1 → 隱藏層2nn.ReLU(),nn.Linear(5, 5),  # 隱藏層2 → 隱藏層3nn.ReLU(),nn.Linear(5, 3)   # 隱藏層3 → 輸出層（3類別，對應One-Hot編碼）)def forward(self, x):"""前向傳播：輸入數據→網絡計算→輸出預測值"""return self.net(x)# 初始化模型（自動運行在CPU，因未指定設備）
model = DNN()# ======================== 3. 定義訓練參數 ======================== #
epochs = 1000                # 訓練輪次：整個數據集遍歷1000次
loss_fn = nn.MSELoss()       # 損失函數：均方誤差（適合One-Hot編碼的分類任務）
optimizer = optim.SGD(       # 優化器：隨機梯度下降model.parameters(),      # 優化對象：模型的權重和偏置lr=0.01                  # 學習率：控制參數更新幅度（需根據任務調整）
)# 提取訓練集的輸入（前3列）和輸出（后3列）
X_train = train_data[:, :3]
Y_train = train_data[:, 3:]# ======================== 4. 訓練網絡 ======================== #
loss_recorder = []  # 記錄每輪損失，用于分析訓練趨勢
for epoch in range(epochs):# 1. 前向傳播：用當前模型預測訓練數據pred = model(X_train)# 2. 計算損失：預測值與真實值的差距loss = loss_fn(pred, Y_train)loss_recorder.append(loss.item())  # 保存損失值（轉換為Python數值）# 3. 反向傳播：計算梯度并更新參數optimizer.zero_grad()  # 清空上一輪的梯度（否則會累積，導致錯誤）loss.backward()        # 反向傳播：自動計算參數的梯度optimizer.step()       # 根據梯度更新參數（權重和偏置）# 可選：每100輪打印訓練進度if (epoch + 1) % 100 == 0:print(f"訓練輪次: {epoch+1:4d} / {epochs}, 損失值: {loss.item():.6f}")# ======================== 5. 測試網絡 ======================== #
# 提取測試集的輸入和輸出
X_test = test_data[:, :3]
Y_test = test_data[:, 3:]with torch.no_grad():  # 測試階段無需計算梯度，加速運算并節省內存# 前向傳播預測pred_test = model(X_test)# 將預測值規整為One-Hot格式（與真實標簽一致）# 步驟：找到每個樣本預測值最大的索引，將該位置設為1，其余設為0max_index = torch.argmax(pred_test, dim=1)  # 每個樣本的最大概率類別索引pred_onehot = torch.zeros_like(pred_test)   # 初始化全0的One-Hot張量# 根據索引設置1（dim=1表示按列操作，unsqueeze將索引轉為列向量）pred_onehot.scatter_(1, max_index.unsqueeze(1), 1)# 計算準確率：預測與真實完全匹配的樣本數 ÷ 總樣本數correct_count = torch.sum(torch.all(pred_onehot == Y_test, dim=1))  # 逐樣本判斷是否全對total_count = Y_test.shape[0]accuracy = 100 * correct_count / total_countprint(f"\n測試集準確率: {accuracy:.2f} %")# ======================== 6. 保存模型 ======================== #
torch.save(model, "dnn_model.pth")
print("模型已保存為 'dnn_model.pth'（可后續加載復用）")

運行結果如下：

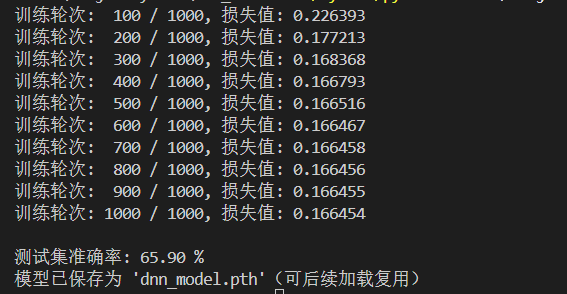
在這里插入圖片描述
從最終結果上來看，損失從 0.226 逐步降至 0.166，符合梯度下降的收斂規律：

前期（1~300 輪）：損失快速下降 → 模型快速學習輸入（X1/X2/X3）和輸出（區間分類）的關聯；
后期（300~1000 輪）：損失下降變緩 → 接近局部最優解，參數調整空間縮小
可以理解為模型學不動了。

最終損失仍較高，說明模型未完全擬合數據，

不過考慮到本次模型結構簡單，我們只用了3 層隱藏層，每層僅 5 個神經元，再加上優化器（SGD）較基礎，沒有換更智能的優化器，所以這個結果也不意外。

4 批量梯度下降

上一章實現了基礎DNN，但未明確梯度下降的批量處理方式。批量梯度下降（BGD）每次用全部樣本更新參數，適用于小數據集。本章將完整演示其流程。

4.1 制作數據集

從Excel導入數據，轉換為張量并劃分訓練集和測試集。

import pandas as pd# 導入數據并轉換為張量
df = pd.read_csv('Data.csv', index_col=0)
arr = df.values.astype(np.float32)  # 轉為float32避免類型沖突
ts = torch.tensor(arr).to('cuda')  # 遷移到GPU# 劃分訓練集（70%）和測試集（30%）
ts = ts[torch.randperm(ts.size(0)), :]
train_size = int(len(ts) * 0.7)
train_Data = ts[:train_size, :]
test_Data = ts[train_size:, :]

4.2 搭建神經網絡

輸入特征為8個，輸出特征為1個，網絡結構如下：

class DNN(nn.Module):def __init__(self):super(DNN, self).__init__()self.net = nn.Sequential(nn.Linear(8, 32), nn.Sigmoid(),  # 8→32神經元，Sigmoid激活nn.Linear(32, 8), nn.Sigmoid(),nn.Linear(8, 4), nn.Sigmoid(),nn.Linear(4, 1), nn.Sigmoid()  # 輸出層1個神經元)def forward(self, x):return self.net(x)model = DNN().to('cuda:0')

這里的原理在上一節有做過圖進行演示，道理是一樣的。

self.net = nn.Sequential(nn.Linear(8, 32), nn.Sigmoid(),  # 8→32神經元，Sigmoid激活nn.Linear(32, 8), nn.Sigmoid(),nn.Linear(8, 4), nn.Sigmoid(),nn.Linear(4, 1), nn.Sigmoid()  # 輸出層1個神經元
)

然后這里使用sigmoid激活則是為引入非線性，避免多層線性層退化為單層，讓網絡學習復雜特征，雖然存在梯度消失缺陷，但因本網絡隱藏層少、任務簡單，故仍采用；

4.3 訓練網絡

使用BGD（每次輸入全部訓練樣本）：

loss_fn = nn.BCELoss(reduction='mean')  # 二分類損失函數
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)  # Adam優化器
epochs = 5000
losses = []# 提取訓練集輸入和輸出
X = train_Data[:, :-1]
Y = train_Data[:, -1].reshape((-1, 1))  # 調整輸出形狀for epoch in range(epochs):Pred = model(X)loss = loss_fn(Pred, Y)losses.append(loss.item())optimizer.zero_grad()loss.backward()optimizer.step()

4.4 測試網絡

X = test_Data[:, :-1]
Y = test_Data[:, -1].reshape((-1, 1))with torch.no_grad():Pred = model(X)Pred[Pred >= 0.5] = 1  # 預測值≥0.5視為1，否則為0Pred[Pred < 0.5] = 0correct = torch.sum((Pred == Y).all(1))total = Y.size(0)print(f'測試集精準度: {100 * correct / total} %')

4.5 完整程序

注意：這里仍然是用CPU來運行的，想改成GPU的，ts = torch.tensor(arr)這個程序指定好你得cuda即可，程序后面的也是如此。

import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np  # 用于數組類型轉換# ======================== 1. 制作數據集 ======================== #
# 從xlsx讀取數據
df = pd.read_excel(r'D:\ProjectPython\DNN_CNN\Data.xlsx', index_col=0,engine='openpyxl')  
# 轉換為float32（PyTorch默認浮點類型，避免類型沖突）
arr = df.values.astype(np.float32)  
# 轉換為PyTorch張量（自動運行在CPU，因未指定device）
ts = torch.tensor(arr)  # 打亂數據順序（避免訓練時樣本順序影響模型學習）
shuffled_idx = torch.randperm(ts.size(0))  # 生成隨機索引
ts = ts[shuffled_idx]# 劃分訓練集（70%）和測試集（30%）
train_size = int(len(ts) * 0.7)
train_Data = ts[:train_size]  # 前70%為訓練集
test_Data = ts[train_size:]   # 后30%為測試集# ======================== 2. 搭建神經網絡 ======================== #
class DNN(nn.Module):def __init__(self):super(DNN, self).__init__()# 構建4層全連接網絡，Sigmoid作為激活函數self.net = nn.Sequential(# 輸入層：8個特征 → 隱藏層1：32個神經元nn.Linear(8, 32), nn.Sigmoid(),  # 隱藏層1 → 隱藏層2：8個神經元nn.Linear(32, 8), nn.Sigmoid(),   # 隱藏層2 → 隱藏層3：4個神經元nn.Linear(8, 4), nn.Sigmoid(),    # 隱藏層3 → 輸出層：1個神經元（輸出概率，范圍0~1）nn.Linear(4, 1), nn.Sigmoid()     )def forward(self, x):"""前向傳播：輸入數據通過網絡計算，返回預測概率"""return self.net(x)# 初始化模型（自動運行在CPU）
model = DNN()  # ======================== 3. 訓練配置（超參數） ======================== #
loss_fn = nn.BCELoss(reduction='mean')  # 二分類交叉熵損失（適配Sigmoid的概率輸出）
optimizer = optim.Adam(  # Adam優化器（收斂更快，適合演示）model.parameters(),  # 優化對象：模型的權重和偏置lr=0.005             # 學習率：控制參數更新幅度
)
epochs = 5000  # 訓練輪次：整個訓練集遍歷5000次
losses = []    # 記錄每輪損失，用于分析訓練趨勢# ======================== 4. 訓練網絡 ======================== #
# 提取訓練集的輸入（前8列）和輸出（最后1列，需調整形狀為[batch, 1]）
X_train = train_Data[:, :-1]
Y_train = train_Data[:, -1].reshape(-1, 1)  # 確保輸出是二維張量（匹配BCELoss輸入要求）for epoch in range(epochs):# 1. 前向傳播：用當前模型預測訓練數據pred = model(X_train)# 2. 計算損失：預測概率與真實標簽的差距loss = loss_fn(pred, Y_train)losses.append(loss.item())  # 保存損失值（轉換為Python原生浮點數）# 3. 反向傳播 + 參數更新optimizer.zero_grad()  # 清空上一輪的梯度（否則會累積，導致錯誤）loss.backward()        # 自動計算參數的梯度（反向傳播）optimizer.step()       # 根據梯度更新參數（權重和偏置）# 可選：每500輪打印訓練進度（方便觀察收斂情況）if (epoch + 1) % 500 == 0:print(f"訓練輪次: {epoch+1:5d} / {epochs}, 當前損失: {loss.item():.6f}")# ======================== 5. 測試網絡 ======================== #
# 提取測試集的輸入和輸出（同樣調整輸出形狀）
X_test = test_Data[:, :-1]
Y_test = test_Data[:, -1].reshape(-1, 1)with torch.no_grad():  # 測試階段無需計算梯度，提升效率并節省內存# 前向傳播預測pred_test = model(X_test)# 將概率預測轉換為0/1（≥0.5視為正類，<0.5視為負類）pred_test[pred_test >= 0.5] = 1.0pred_test[pred_test < 0.5] = 0.0# 計算準確率：預測與真實完全一致的樣本數 ÷ 總樣本數# torch.all(..., dim=1)：逐行判斷所有列是否都匹配（此處僅1列，即判斷單個值是否相等）correct_count = torch.sum(torch.all(pred_test == Y_test, dim=1))total_count = Y_test.size(0)accuracy = 100 * correct_count / total_countprint(f"\n測試集準確率: {accuracy:.2f} %")

運行結果如下：

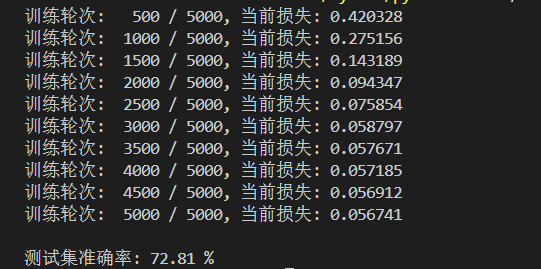
在這里插入圖片描述
從輸出的結果上來說，訓練時損失從0.4203逐步降至0.0567，前期快速下降、后期收斂趨緩，體現模型有效學習數據關聯但逼近優化瓶頸。后續可通過替換ReLU激活、采用AdamW + 學習率調度優化訓練、分析數據平衡與特征質量等方式突破性能瓶頸。

5 小批量梯度下降

批量梯度下降在大數據集上效率低，小批量梯度下降（MBGD）按批次輸入樣本，平衡效率和穩定性。本章將使用PyTorch的DataSet和DataLoader實現MBGD。

5.1 制作數據集

繼承Dataset類封裝數據，實現數據加載、索引獲取和長度計算。

from torch.utils.data import Dataset, DataLoader, random_splitclass MyData(Dataset):def __init__(self, filepath):df = pd.read_csv(filepath, index_col=0)arr = df.values.astype(np.float32)ts = torch.tensor(arr).to('cuda')self.X = ts[:, :-1]  # 輸入特征self.Y = ts[:, -1].reshape((-1, 1))  # 輸出特征self.len = ts.shape[0]  # 樣本總數def __getitem__(self, index):return self.X[index], self.Y[index]  # 獲取索引對應的樣本def __len__(self):return self.len  # 返回樣本總數# 劃分訓練集和測試集
Data = MyData('Data.csv')
train_size = int(len(Data) * 0.7)
test_size = len(Data) - train_size
train_Data, test_Data = random_split(Data, [train_size, test_size])# 批次加載器（shuffle=True表示每個epoch前打亂數據）
train_loader = DataLoader(dataset=train_Data, shuffle=True, batch_size=128)
test_loader = DataLoader(dataset=test_Data, shuffle=False, batch_size=64)

5.2 搭建神經網絡

與4.2節結構相同（輸入8，輸出1）。

5.3 訓練網絡

按批次輸入樣本進行訓練：

loss_fn = nn.BCELoss(reduction='mean')
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)
epochs = 500
losses = []for epoch in range(epochs):for (x, y) in train_loader:  # 按批次獲取樣本Pred = model(x)loss = loss_fn(Pred, y)losses.append(loss.item())optimizer.zero_grad()loss.backward()optimizer.step()

5.4 測試網絡

按批次測試并計算總準確率：

correct = 0
total = 0
with torch.no_grad():for (x, y) in test_loader:Pred = model(x)Pred[Pred >= 0.5] = 1Pred[Pred < 0.5] = 0correct += torch.sum((Pred == y).all(1))total += y.size(0)
print(f'測試集精準度: {100 * correct / total} %')

5.5 完整程序

# 導入必要庫
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader, random_split
import numpy as np# ======================== 1. 自定義數據集類（支持.xlsx） ======================== #
class MyData(Dataset):def __init__(self, filepath):"""初始化：讀取Excel數據，轉換為PyTorch張量（CPU）:param filepath: 數據集文件路徑（.xlsx格式）"""# 讀取Excel（必須安裝openpyxl！engine指定解析器）df = pd.read_excel(  filepath, index_col=0,        # 第1列作為索引engine='openpyxl'   # 強制使用openpyxl解析.xlsx)  arr = df.values.astype(np.float32)  # 轉換為float32（匹配PyTorch）ts = torch.tensor(arr)              # 轉為CPU張量（未指定device的情況下不使用GPU）self.X = ts[:, :-1]  # 輸入特征（前8列）self.Y = ts[:, -1].reshape(-1, 1)  # 輸出標簽（最后1列，調整為列向量）self.len = len(ts)   # 樣本總數def __getitem__(self, index):"""獲取指定索引的樣本：(輸入特征, 輸出標簽)"""return self.X[index], self.Y[index]def __len__(self):"""返回數據集總樣本數"""return self.len# ======================== 2. 加載并劃分數據集 ======================== #
data_path = "Data.xlsx"  # 改為你的Excel文件路徑（確保存在）
full_dataset = MyData(data_path)  # 初始化自定義數據集# 劃分訓練集（70%）和測試集（30%）
train_size = int(0.7 * len(full_dataset))
test_size = len(full_dataset) - train_size
train_dataset, test_dataset = random_split(full_dataset, [train_size, test_size])# 創建數據加載器（小批量讀取）
batch_size = 128  # 小批量大小（可調整，建議2的冪次）
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True  # 訓練集每個epoch前打亂
)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False  # 測試集保持順序，方便復現
)# ======================== 3. 定義神經網絡模型 ======================== #
class DNN(nn.Module):def __init__(self):super(DNN, self).__init__()# 4層全連接網絡，Sigmoid激活（輸出層適配二分類）self.net = nn.Sequential(nn.Linear(8, 32), nn.Sigmoid(),  # 8→32nn.Linear(32, 8), nn.Sigmoid(),   # 32→8nn.Linear(8, 4), nn.Sigmoid(),    # 8→4nn.Linear(4, 1), nn.Sigmoid()     # 4→1（輸出0~1概率）)def forward(self, x):"""前向傳播：輸入→網絡→預測概率"""return self.net(x)model = DNN()  # CPU運行# ======================== 4. 訓練配置（損失函數 + 優化器） ======================== #
loss_fn = nn.BCELoss(reduction='mean')  # 二分類交叉熵損失
optimizer = optim.Adam(model.parameters(), lr=0.005)  # Adam優化器
epochs = 500  # 訓練輪次
losses = []   # 記錄batch級損失# ======================== 5. 小批量訓練（MBGD） ======================== #
for epoch in range(epochs):for batch_idx, (x, y) in enumerate(train_loader):# 1. 前向傳播pred = model(x)# 2. 計算損失loss = loss_fn(pred, y)losses.append(loss.item())# 3. 反向傳播 + 更新參數optimizer.zero_grad()  # 清空梯度loss.backward()        # 計算梯度optimizer.step()       # 更新參數# 每100輪打印進度if (epoch + 1) % 100 == 0:print(f"訓練輪次: {epoch+1:4d} / {epochs}, 最近批次損失: {loss.item():.6f}")# ======================== 6. 測試網絡 ======================== #
correct = 0
total = 0with torch.no_grad():  # 關閉梯度，加速測試for x, y in test_loader:pred = model(x)# 概率→0/1（閾值0.5）pred[pred >= 0.5] = 1.0pred[pred < 0.5] = 0.0# 統計正確數（逐樣本判斷）batch_correct = torch.sum(torch.all(pred == y, dim=1))correct += batch_correct.item()total += y.size(0)accuracy = 100 * correct / total
print(f"\n測試集準確率: {accuracy:.2f} %")

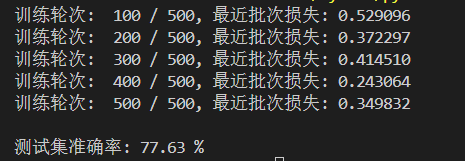
運行結果如下：

在這里插入圖片描述

6 手寫數字識別

前幾章介紹了通用DNN的實現，本章以**MNIST數據集（手寫數字圖像）**為例，展示DNN在圖像分類任務中的應用。

6.1 制作數據集

使用torchvision下載MNIST數據集，轉換為張量并標準化。

from torchvision import transforms, datasets# 數據轉換：轉為張量并標準化（均值0.1307，標準差0.3081）
transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize(0.1307, 0.3081)
])# 下載訓練集和測試集
train_Data = datasets.MNIST(root='D:/Jupyter/dataset/mnist/',train=True, download=True, transform=transform
)
test_Data = datasets.MNIST(root='D:/Jupyter/dataset/mnist/',train=False, download=True, transform=transform
)# 批次加載器
train_loader = DataLoader(train_Data, shuffle=True, batch_size=64)
test_loader = DataLoader(test_Data, shuffle=False, batch_size=64)

6.2 搭建神經網絡

輸入為28×28的圖像（展平為784維），輸出為10個數字（0-9）：

class DNN(nn.Module):def __init__(self):super(DNN, self).__init__()self.net = nn.Sequential(nn.Flatten(),  # 展平圖像為784維向量nn.Linear(784, 512), nn.ReLU(),nn.Linear(512, 256), nn.ReLU(),nn.Linear(256, 128), nn.ReLU(),nn.Linear(128, 64), nn.ReLU(),nn.Linear(64, 10)  # 輸出10個類別)def forward(self, x):return self.net(x)model = DNN().to('cuda:0')

6.3 訓練網絡

使用交叉熵損失（自帶softmax激活）和帶動量的SGD優化器：

loss_fn = nn.CrossEntropyLoss()  # 多分類損失函數
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 動量參數
epochs = 5
losses = []for epoch in range(epochs):for (x, y) in train_loader:x, y = x.to('cuda:0'), y.to('cuda:0')  # 遷移到GPUPred = model(x)loss = loss_fn(Pred, y)losses.append(loss.item())optimizer.zero_grad()loss.backward()optimizer.step()

6.4 測試網絡

correct = 0
total = 0
with torch.no_grad():for (x, y) in test_loader:x, y = x.to('cuda:0'), y.to('cuda:0')Pred = model(x)_, predicted = torch.max(Pred.data, dim=1)  # 獲取預測類別（最大值索引）correct += torch.sum(predicted == y)total += y.size(0)
print(f'測試集精準度: {100 * correct / total} %')

6.5 完整程序

# 導入核心庫
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import transforms, datasets  # 用于加載MNIST數據集
from torch.utils.data import DataLoader       # 用于批量加載數據# ======================== 1. 數據集準備（MNIST） ======================== #
# 數據預處理：轉為張量 + 標準化（均值和標準差是MNIST的統計特征，加速訓練收斂）
transform = transforms.Compose([transforms.ToTensor(),  # 將PIL圖像轉為張量（自動縮放到[0,1]）transforms.Normalize(   # 標準化：(x-mean)/std，減少數據分布差異對訓練的影響mean=0.1307,        # MNIST像素均值（官方推薦的參數）std=0.3081          # MNIST像素標準差（官方推薦的參數）)
])# 下載并加載訓練集（自動下載到root目錄，train=True表示訓練集）
train_dataset = datasets.MNIST(root='./data/mnist',     # 數據保存路徑（不存在則自動創建）train=True,              # 加載訓練集download=True,           # 自動下載transform=transform      # 應用預處理
)# 下載并加載測試集（train=False表示測試集）
test_dataset = datasets.MNIST(root='./data/mnist',     train=False,             download=True,           transform=transform      
)# 創建批量加載器（小批量梯度下降，提升效率）
batch_size = 64  # 每批64張圖像
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True  # 訓練集打亂，增加隨機性
)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False  # 測試集保持順序，方便結果復現
)# ======================== 2. 定義神經網絡模型 ======================== #
class DNN(nn.Module):def __init__(self):super(DNN, self).__init__()self.net = nn.Sequential(nn.Flatten(),  # 將28×28的圖像展平為784維向量（28*28=784）# 全連接層 + ReLU激活（逐步壓縮特征維度）nn.Linear(784, 512), nn.ReLU(),  # 784→512nn.Linear(512, 256), nn.ReLU(),  # 512→256nn.Linear(256, 128), nn.ReLU(),  # 256→128nn.Linear(128, 64),  nn.ReLU(),  # 128→64nn.Linear(64, 10)                # 64→10（輸出10個數字的預測概率）)def forward(self, x):"""前向傳播：輸入圖像→網絡→10類預測概率"""return self.net(x)# 初始化模型（默認運行在CPU，無需顯式指定設備）
model = DNN()  # ======================== 3. 訓練配置（損失函數 + 優化器） ======================== #
loss_fn = nn.CrossEntropyLoss()  # 多分類交叉熵損失（自帶Softmax，輸出層無需激活）
optimizer = optim.SGD(           # 帶動量的隨機梯度下降（加速收斂）model.parameters(),          # 優化對象：模型參數lr=0.01,                     # 學習率momentum=0.5                 # 動量（利用歷史梯度加速更新）
)
epochs = 5  # 訓練輪次（遍歷整個訓練集5次）# ======================== 4. 訓練網絡 ======================== #
for epoch in range(epochs):# 遍歷訓練集的每個批次for batch_idx, (images, labels) in enumerate(train_loader):# 1. 前向傳播：計算當前批次的預測概率outputs = model(images)# 2. 計算損失：預測與真實標簽的差距loss = loss_fn(outputs, labels)# 3. 反向傳播 + 參數更新optimizer.zero_grad()  # 清空上一輪梯度loss.backward()        # 反向傳播計算梯度optimizer.step()       # 更新模型參數# 每輪結束打印進度（觀察損失變化，可選）print(f"訓練輪次: {epoch+1}/{epochs}, 最近批次損失: {loss.item():.4f}")# ======================== 5. 測試網絡 ======================== #
correct = 0  # 正確預測的樣本數
total = 0    # 測試集總樣本數with torch.no_grad():  # 測試階段關閉梯度計算，提升效率for images, labels in test_loader:# 前向傳播預測outputs = model(images)# 獲取預測類別（取概率最大的索引，dim=1表示按行取最大值）_, predicted = torch.max(outputs.data, dim=1)# 統計正確數和總數correct += (predicted == labels).sum().item()total += labels.size(0)# 計算準確率
accuracy = 100 * correct / total
print(f"\n測試集準確率: {accuracy:.2f} %")

運行結果如下：

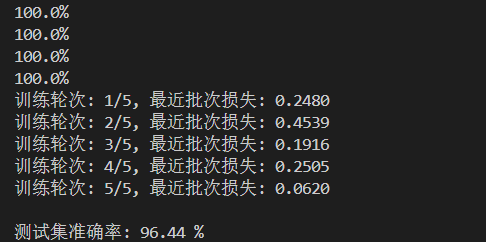
在這里插入圖片描述
訓練中損失從0.2480震蕩降至0.0620，體現模型有效學習但受小批量隨機性影響；測試集96.44%準確率達到DNN基線，證明能夠很好地去捕捉數字特征卻存在提升空間。可通過延長訓練輪次、換Adam優化器/加學習率調度加速收斂，或升級為CNN利用圖像空間關聯，突破性能瓶頸。不過這個準確率已經算是可以了。