本教程介紹 CS61B 中的基數排序，這是一種可以在某些情況下甚至超越歸并排序、快速排序的特殊的排序方法，但是犧牲了內存空間

計數排序

連續編號情形

我們需要對一個編號從 0 到 11 的表進行排序

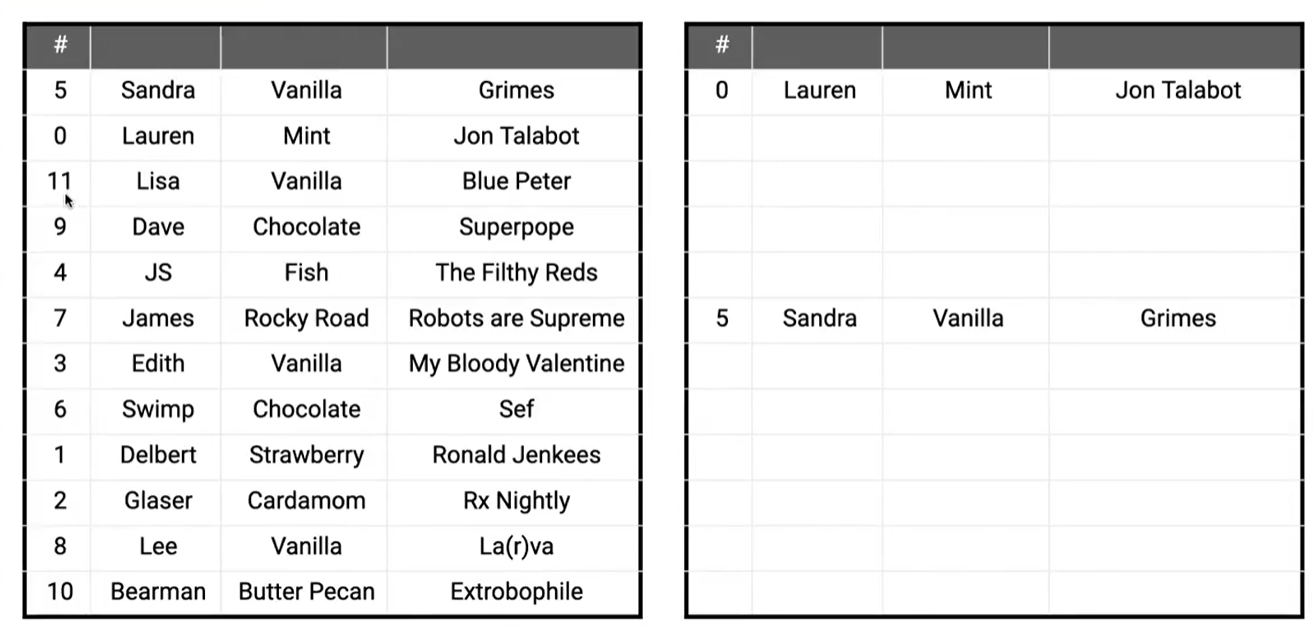
實際上我們可以拿出另一張同樣大小的空白表，在遍歷左邊表時，我們不需要進行比較，就可以直接將元素填到正確的位置上！

這樣我們的時間復雜度來到了 $\theta (N)$，避免了之前我們提到的 $NlogN$ 界限
但這種情況你必須保證編號是連續的

花色分類情形

我們要考慮的問題是，我怎么知道第一個紅桃應該放在哪里呢？
我們要做的是，掃描兩次，第一次掃描來計數每個相同的元素有多少個（同時根據優先級，我們可以知道每個元素的索引是多少），第二次掃描根據第一次掃描的結果來進行放置。

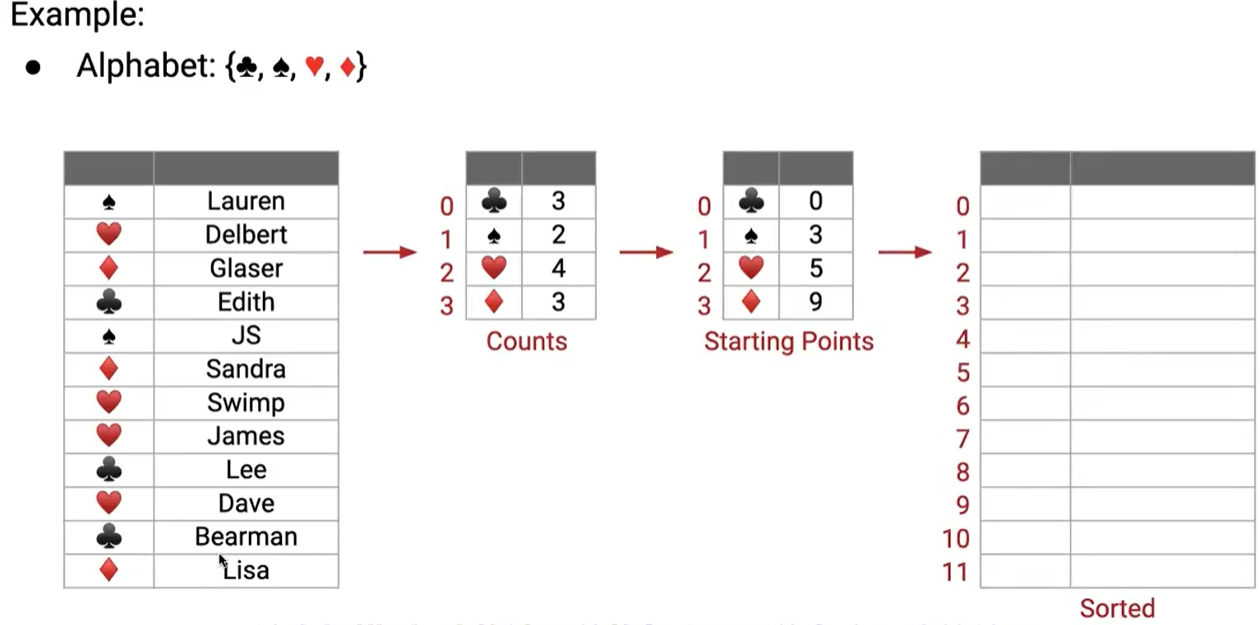
經過第一次掃描后，我可以根據counts表，得出這樣一個 Starting Points 的元素索引表，來記錄下一個對應的元素應該放置在哪個索引處，每次放置之后，更新索引表中的對應元素

計數排序 vs 快速排序

考慮城市人口排名的情形，城市人口是不連續的，如果在這里我們使用計數排序的話，需要列一個非常非常大的計數表

計數排序

實際上我需要兩個變量來表示計數排序，一個用于告訴我元素的數量在增加，第二個變量告訴我，字母表的大小在增加
在花色分類中，字母表大小為4，而在城市人口排名中，字母表的大小為3700萬

這樣問題可以以兩種不同方式增長
如果我們有 k 個不同的種類，而字母表大小為 R，那么時間復雜度為 $\theta (N+R)$ ，空間使用情況仍然為 $\theta (N+R)$
（時間復雜度中的 R 來源于我在第一次遍歷數組之后，還需要遍歷 R 數組將對應的索引填進去）

基數排序

LSD

我們可以將每一個編號看作一個數字或者具有不同位數的元素
我們從最低有效位開始排序，然后逐步向最高有效位排序，同時每次排序保證是穩定的（也就是相同的數字，相對位置保持不變）

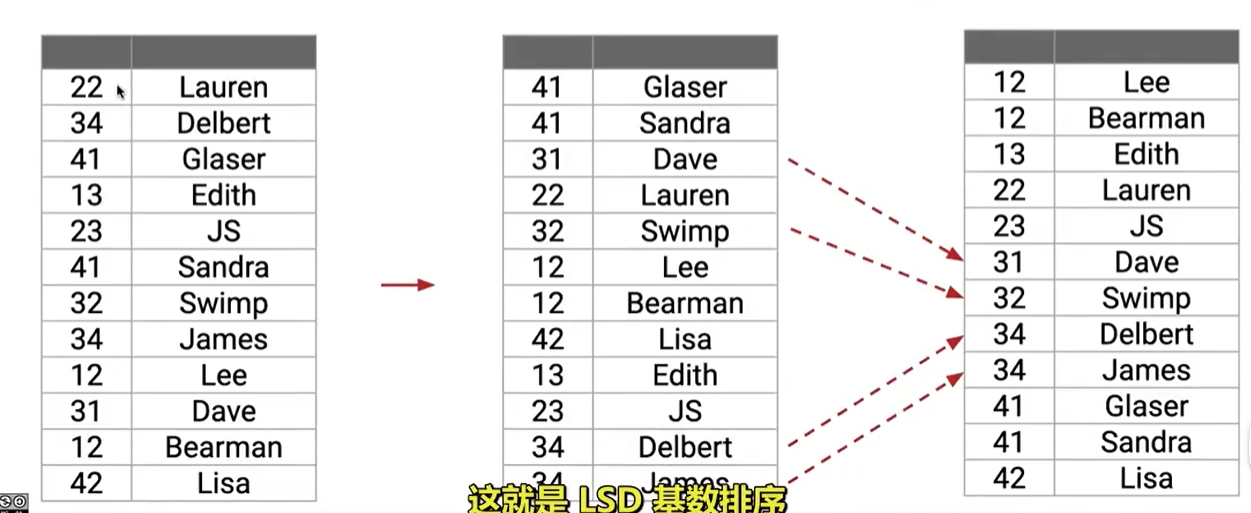
這樣我們的時間復雜度為 $\theta (W(N+R))$
其中 N 表示元素的數量，R 表示字母表的大小，W 表示元素的寬度（位數）
相當于對每一位都進行一次計數排序

MSD

但是如果我的字符串非常長，那么 LSD 可能就會變得很慢，歸并排序不會在較長的字符串上變慢，因為必須比較所有字符

我們可以從最高有效位開始比較
但是 MSD 會出現不穩定的情況

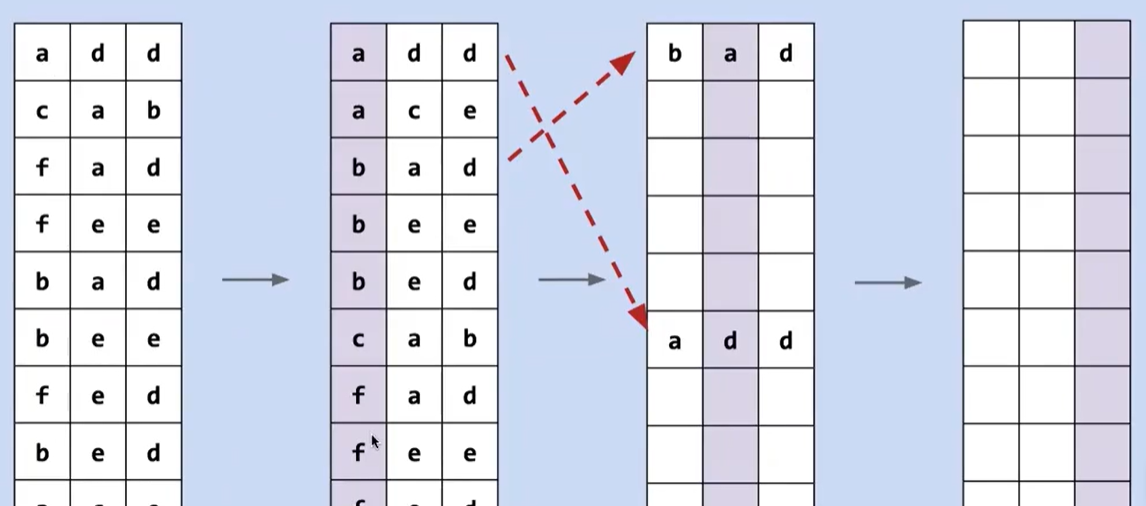
這樣直接從最高位開始進行排序，會因為不穩定導致排序錯誤
為此，我們可以將其分解成子問題，比如一旦將所有以 a 開頭的單詞歸類，下一步將是對這個子問題進行排序，而這些元素不會越界到 b 的范圍

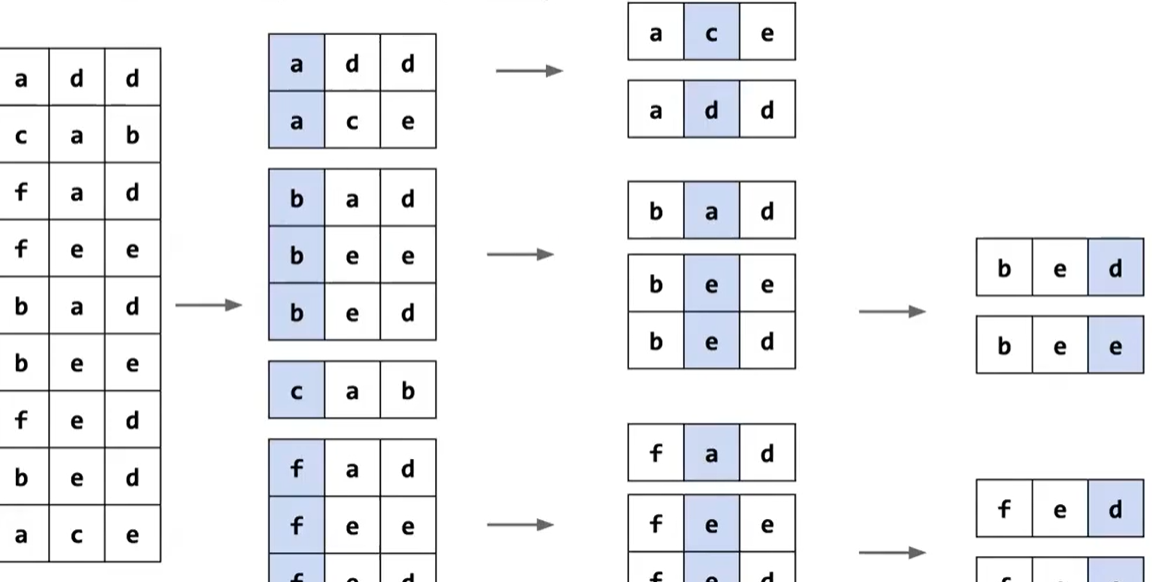
MSD 的時間復雜度有不同的情況

• 最好情況：比較最高位即完成，$\theta (N+R)$
• 最壞情況：需要比較每一位，退化成 LSD ，$\theta (WN+WR)$

LSD vs Merge Sort

實際情況；

• 我們認為字母表是常數，LSD 時間復雜度為 $\theta (WN)$
• 歸并排序在 $\theta (NlogN)$ 到 $\theta (WNlogN)$ 之間

而具體來說哪一個更好呢？這取決于實際情況

• LSD 更快
  • N非常非常大
  • 比較的字符串之間非常相似
  • 
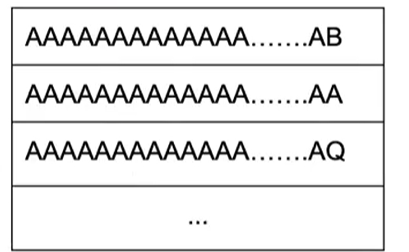
• 歸并排序更快
  • 比較的字符串之間差異非常大
  •