7.10 舒爾函數的組合定義
前幾節討論的四個基 mλm_{\lambda}mλ?、eλe_{\lambda}eλ?、hλh_{\lambda}hλ? 和 pλp_{\lambda}pλ? 的定義都較為直觀。本節將介紹第五個基,其元素記為 sλs_{\lambda}sλ?,稱為舒爾函數,其定義則更為微妙。實際上,舒爾函數有許多不同的(等價的)定義方式,例如可以通過前述四個基中的任意一個來定義,或通過涉及行列式商的“經典”定義,或通過與正交性和三角化相關的抽象性質,又或通過更高級的代數方法。對于初學者而言,這些定義可能都顯得缺乏動機。我們選擇通過 mλm_{\lambda}mλ? 來定義 sλs_{\lambda}sλ?,因為這種方法最具組合性,盡管其他方法也有其獨特的優勢。當然,最終所有這些方法都會導向相同的理論。
舒爾函數的重要性很大程度上源于它們與數學其他分支的聯系,例如表示論和代數幾何。我們將在第7.18節討論其與對稱群 Sn\mathfrak{S}_nSn? 的表示論的聯系,并在附錄2中討論其與一般線性群 GL?(n,C)\operatorname{GL}(n, \mathbb{C})GL(n,C) 及相關群的聯系。舒爾函數的另一個重要應用(本書未展開)是Schubert演算;Grassmann簇 Gk(Cn)G_{k}(\mathbb{C}^n)Gk?(Cn) 的上同調環可以用舒爾函數自然地描述。
對稱函數
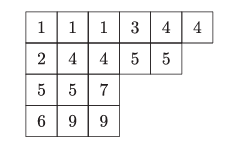
與舒爾函數相關的基本組合對象是半標準楊表。設 λ\lambdaλ 是一個分劃。一個形狀為 λ\lambdaλ 的半標準楊表(SSYT)是一個由正整數構成的數組 T=(Tij)T = (T_{ij})T=(Tij?),其形狀為 λ\lambdaλ(即 1≤i≤?(λ)1 \leq i \leq \ell(\lambda)1≤i≤?(λ),1≤j≤λi1 \leq j \leq \lambda_i1≤j≤λi?),且滿足每行弱遞增、每列嚴格遞增。半標準楊表的大小是其條目數。以下是一個形狀為 (6,5,3,3)(6,5,3,3)(6,5,3,3) 的半標準楊表的例子:
11122322334456667 \begin{array}{cccccc} 1 & 1 & 1 & 2 & 2 & 3 \\ 2 & 2 & 3 & 3 & 4 & \\ 4 & 5 & 6 & & & \\ 6 & 6 & 7 & & & \\ \end{array} 1246?1256?1367?23?24?3?
若 $ T $ 是一個形狀為 λ\lambdaλ 的半標準楊表(SSYT),則記 λ=sh(T)\lambda = \text{sh}(T)λ=sh(T)。因此,$ T $ 的大小即為 ∣sh(T)∣|\text{sh}(T)|∣sh(T)∣。我們也可以將形狀為 λ\lambdaλ 的半標準楊表視為 λ\lambdaλ 的楊圖(如第1.7節所定義),其方格中填入了滿足特定條件的正整數。例如,上述半標準楊表可表示為:
若 $ T $ 中有 αi=αi(T)\alpha_i = \alpha_i(T)αi?=αi?(T) 個部分等于 iii,則稱 $ T $ 的類型為 α=(α1,α2,…)\alpha = (\alpha_1, \alpha_2, \ldots)α=(α1?,α2?,…),記作 α=type(T)\alpha = \text{type}(T)α=type(T)。因此,上述半標準楊表的類型為 (3,1,1,4,4,1,1,0,2)(3, 1, 1, 4, 4, 1, 1, 0, 2)(3,1,1,4,4,1,1,0,2)。對于任何類型為 α\alphaα 的半標準楊表 $ T $(或實際上任何帶有額外結構的 P\mathbb{P}P 上的多重集),記
xT=x1α1(T)x2α2(T)??. x^T = x_{1}^{\alpha_1(T)} x_{2}^{\alpha_2(T)} \cdots. xT=x1α1?(T)?x2α2?(T)??.
對于上述例子,有
xT=x13x2x44x54x6x7x92. x^T = x_{1}^3 x_{2} x_{4}^4 x_{5}^4 x_{6} x_{7} x_{9}^2. xT=x13?x2?x44?x54?x6?x7?x92?.
半標準楊表的定義可以自然地推廣到對稱函數理論中的斜形狀。若 λ\lambdaλ 和 μ\muμ 是滿足 μ?λ\mu \subseteq \lambdaμ?λ(即對所有 iii 有 μi≤λi\mu_i \leq \lambda_iμi?≤λi?)的分劃,則定義形狀為 λ/μ\lambda / \muλ/μ 的斜半標準楊表為一個由正整數構成的數組 T=(Tij)T = (T_{ij})T=(Tij?),其形狀為 λ/μ\lambda / \muλ/μ(即 1≤i≤?(λ)1 \leq i \leq \ell(\lambda)1≤i≤?(λ),μi<j≤λi\mu_i < j \leq \lambda_iμi?<j≤λi?),且滿足每行弱遞增、每列嚴格遞增。以下是一個形狀為 (6,5,3,3)/(3,1)(6, 5, 3, 3)/(3, 1)(6,5,3,3)/(3,1) 的斜半標準楊表的例子:
3441477226388 \begin{array}{cccccc}& & & 3 & 4 & 4\\& 1 & 4 & 7 & 7 \\ 2 & 2 & 6 & & \\ 3 & 8 & 8 & & \\ \end{array} 23?128?468?37?47?4
類似地,可以將形狀為 λ\lambdaλ 的楊圖的定義推廣到形狀為 λ/μ\lambda / \muλ/μ 的斜楊圖。因此,形狀為 (6,5,3,3)/(3,1)(6, 5, 3, 3)/(3, 1)(6,5,3,3)/(3,1) 的斜楊圖可表示為:
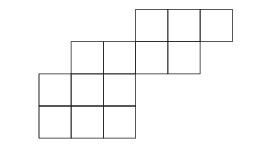
因此,形狀為 λ/μ\lambda / \muλ/μ 的斜半標準楊表可以視為斜楊圖的方格中填入了滿足特定條件的正整數,正如“普通形狀”(也稱為直形狀)λ\lambdaλ 的情況。例如,上述形狀為 (6,5,3,3)/(3,1)(6, 5, 3, 3)/(3, 1)(6,5,3,3)/(3,1) 的斜半標準楊表可表示為:
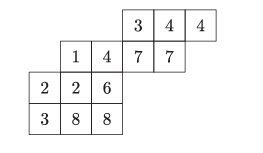
類型 type(T)\text{type}(T)type(T) 和 xTx^TxT 的定義可以直接從普通形狀的半標準楊表推廣到斜形狀的半標準楊表。
現在,我們來到本章的關鍵定義。如前所述,在進一步深入之前,這個定義看起來完全缺乏動機。
7.10.1 定義
設 λ/μ\lambda/\muλ/μ 為斜形狀。變量 x=(x1,x2,…)x=(x_{1},x_{2},\ldots)x=(x1?,x2?,…) 中形狀為 λ/μ\lambda/\muλ/μ 的斜舒爾函數 sλ/μ=sλ/μ(x)s_{\lambda/\mu}=s_{\lambda/\mu}(x)sλ/μ?=sλ/μ?(x) 是形式冪級數
sλ/μ(x)=∑i=1nxi,s_{\lambda/\mu}(x)=\sum_{i=1}^{n}x^{i},sλ/μ?(x)=i=1∑n?xi,
對所有形狀為 λ/μ\lambda/\muλ/μ 的半標準楊表 TTT 求和。若 μ=?\mu=\emptysetμ=? 使得 λ/μ=λ\lambda/\mu=\lambdaλ/μ=λ,則稱 sλ(x)s_{\lambda}(x)sλ?(x) 為形狀 λ\lambdaλ 的舒爾函數。
例如,最大部分不超過 3 的形狀 (2,1)(2,1)(2,1) 的半標準楊表為

因此
s21(x1,x2,x3)=x12x2+x1x22+x12x3+x1x24+x23x3+x2x34+2x1x2x3s_{21}(x_{1},x_{2},x_{3}) = x_{1}^{2}x_{2}+x_{1}x_{2}^{2}+x_{1}^{2}x_{3}+x_{1}x_{2}^{4}+x_{2}^{3}x_{3}+x_{2}x_{3}^{4}+2x_{1}x_{2}x_{3}s21?(x1?,x2?,x3?)=x12?x2?+x1?x22?+x12?x3?+x1?x24?+x23?x3?+x2?x34?+2x1?x2?x3? =m21(x1,x2,x3)+2m111(x1,x2,x3).= m_{21}(x_{1},x_{2},x_{3})+2m_{111}(x_{1},x_{2},x_{3}).=m21?(x1?,x2?,x3?)+2m111?(x1?,x2?,x3?).
因此,由于 s21s_{21}s21? 的每一項中最多出現三個不同的變量,我們有 s21=m21+2m111s_{21}=m_{21}+2m_{111}s21?=m21?+2m111?(作為 Λ\LambdaΛ 的元素,即在無限多變量中的對稱函數)。然而,sλ/μs_{\lambda/\mu}sλ/μ? 實際上總是對稱函數這一點并不顯然。
7.10.2 定理
對任意斜形狀 λ/μ\lambda/\muλ/μ,斜舒爾函數 sλ/μs_{\lambda/\mu}sλ/μ? 是對稱函數。
證明:只需證明 [為什么?] sλ/μs_{\lambda/\mu}sλ/μ? 在交換 xix_{i}xi? 和 xi+1x_{i+1}xi+1? 時保持不變。設 ∣λ/μ∣=n|\lambda/\mu|=n∣λ/μ∣=n,且 α=(α1,α2,…)\alpha=(\alpha_{1},\alpha_{2},\ldots)α=(α1?,α2?,…) 是 nnn 的弱組合。令
α~=(α1,α2,…,αi?1,αi+1,αi,αi+2,…).\tilde{\alpha}=(\alpha_{1},\alpha_{2},\ldots,\alpha_{i-1},\alpha_{i+1},\alpha_{i},\alpha_{i+2},\ldots).α~=(α1?,α2?,…,αi?1?,αi+1?,αi?,αi+2?,…).
若 Tλ/μ,α~\mathcal{T}_{\lambda/\mu,\tilde{\alpha}}Tλ/μ,α~? 表示所有形狀為 λ/μ\lambda/\muλ/μ 且類型為 α\alphaα 的半標準楊表的集合,則我們需要構造一個雙射 φ:Tλ/μ,α→Tλ/μ,α~\varphi:\mathcal{T}_{\lambda/\mu,\alpha}\rightarrow\mathcal{T}_{\lambda/\mu,\tilde{\alpha}}φ:Tλ/μ,α?→Tλ/μ,α~?。
設 T∈Tλ/μ,αT\in\mathcal{T}_{\lambda/\mu,\alpha}T∈Tλ/μ,α?。考慮 TTT 中等于 iii 或 i+1i+1i+1 的部分。TTT 的某些列不包含這些部分,而某些列包含兩個這樣的部分,即一個 iii 和一個 i+1i+1i+1。這些列我們忽略。其余等于 iii 或 i+1i+1i+1 的部分在每列中出現一次,且由一定數量 rrr 個 iii 后跟一定數量 sss 個 i+1i+1i+1 的行組成。(當然,rrr 和 sss 取決于具體的行。)例如,TTT 的一部分可能如下所示。
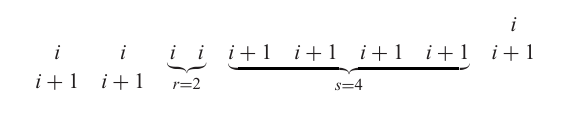
在每一行中,將 rrr 個 ttt 和 sss 個 t+1t+1t+1 轉換為 sss 個 ttt 和 rrr 個 t+1t+1t+1:
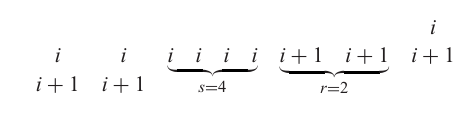
容易看出,得到的數組 φ(T)\varphi(T)φ(T) 屬于 Tλ/μ,α~\mathcal{T}_{\lambda/\mu,\tilde{\alpha}}Tλ/μ,α~?,且 φ\varphiφ 建立了所需的雙射。
若 λ?n\lambda\vdash nλ?n 且 α\alphaα 是 nnn 的弱組合,則記 Kλμ\mathcal{K}_{\lambda\mu}Kλμ? 為形狀 λ\lambdaλ 且類型 α\alphaα 的半標準楊表的數量。Kλα\mathcal{K}_{\lambda\alpha}Kλα? 稱為科斯特卡數(Kostka numbers),在對稱函數理論中具有重要作用。根據定義 7.10.1,我們有
sλ=∑αKλαxα,s_{\lambda}=\sum_{\alpha}\mathcal{K}_{\lambda\alpha}x^{\alpha},sλ?=α∑?Kλα?xα,
對所有 nnn 的弱組合 α\alphaα 求和,因此由定理 7.10.2 可得
sλ=∑μ?nKλμmμ.(7.35)s_{\lambda}=\sum_{\mu\vdash n}\mathcal{K}_{\lambda\mu}m_{\mu}.\qquad\qquad\qquad\qquad(7.35) sλ?=μ?n∑?Kλμ?mμ?.(7.35)
更一般地,我們可以定義斜科斯特卡數 Kλ/ν,α\mathcal{K}_{\lambda/\nu,\alpha}Kλ/ν,α? 為形狀 λ/ν\lambda/\nuλ/ν 且類型 α\alphaα 的半標準楊表的數量,因此若 ∣λ/ν∣=n|\lambda/\nu|=n∣λ/ν∣=n,則
sλ/ν=∑μ?nKλ/ν,μmμ.(7.36)s_{\lambda/\nu}=\sum_{\mu\vdash n}\mathcal{K}_{\lambda/\nu,\mu}m_{\mu}.\qquad\qquad\qquad\qquad(7.36) sλ/ν?=μ?n∑?Kλ/ν,μ?mμ?.(7.36)
目前尚未找到 Kλ/ν,μ\mathcal{K}_{\lambda/\nu,\mu}Kλ/ν,μ? 或甚至 Kλμ\mathcal{K}_{\lambda\mu}Kλμ? 的通用簡單公式,且此類公式存在的可能性較低。對于某些特定的 λ\lambdaλ、ν\nuν 和 μ\muμ,可以給出公式,其中最重要的是 ν=?\nu=\emptysetν=? 且 μ=(1n)\mu=(1^{n})μ=(1n) 的情況。雖然我們將在后續內容中給出此公式(推論 7.21.6),但讓我們更詳細地探討數 Kλ,1n\mathcal{K}_{\lambda,1^{n}}Kλ,1n?(也記作 fλf^{\lambda}fλ)的含義。組合意義。根據定義,fλf^{\lambda}fλ 是將數字 1,2,…,n1,2,\ldots,n1,2,…,n 插入形狀 λ?n\lambda\vdash nλ?n 的方式數,每個數字恰好出現一次,且每行每列嚴格遞增。這樣的數組稱為形狀 λ\lambdaλ 的標準楊表(SYT)(或簡稱標準表)。例如,形狀 (3,2)(3,2)(3,2) 的標準楊表為
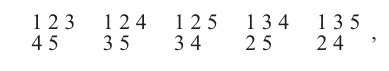
因此 f(3,2)=5f^{(3,2)}=5f(3,2)=5。數 fλf^{\lambda}fλ 還有幾種其他組合解釋,如下述命題所示。
7.10.3 命題
設 λ∈Par\lambda \in \text{Par}λ∈Par。則數 fλf^\lambdafλ 枚舉以下 (a)-(e) 項中的對象。我們以 λ=(3,2)\lambda = (3, 2)λ=(3,2) 為例說明這些對象。
(a) (分劃鏈) Young 格 YYY 的區間 [?,λ][\emptyset, \lambda][?,λ] 中的飽和鏈,等價地,滿足 λi\lambda^iλi 由 λi?1\lambda^{i-1}λi?1 添加單個方格得到的分劃序列 ?=λ0?λ1???λn=λ\emptyset = \lambda^0 \subset \lambda^1 \subset \cdots \subset \lambda^n = \lambda?=λ0?λ1???λn=λ 的數量(我們將分劃與其圖示視為等同):
??1?2?3?31?32??1?2?21?31?32??1?2?21?22?32??1?11?21?31?32??1?11?21?22?32
\begin{aligned}
&\emptyset \subset 1 \subset 2 \subset 3 \subset 31 \subset 32 \\
&\emptyset \subset 1 \subset 2 \subset 21 \subset 31 \subset 32 \\
&\emptyset \subset 1 \subset 2 \subset 21 \subset 22 \subset 32 \\
&\emptyset \subset 1 \subset 11 \subset 21 \subset 31 \subset 32 \\
&\emptyset \subset 1 \subset 11 \subset 21 \subset 22 \subset 32
\end{aligned}
???1?2?3?31?32??1?2?21?31?32??1?2?21?22?32??1?11?21?31?32??1?11?21?22?32?
(b) (線性擴張) 設 PλP_\lambdaPλ? 是偏序集,其元素為 λ\lambdaλ 圖示的方格,若 ttt 位于 sss 正右方或正下方(中間無其他方格)則 ttt 覆蓋 sss。此類偏序集即為 N×N\mathbb{N} \times \mathbb{N}N×N 的有限序理想。則 fλ=e(Pλ)f^\lambda = e(P_\lambda)fλ=e(Pλ?),即 PλP_\lambdaPλ? 的線性擴張數。
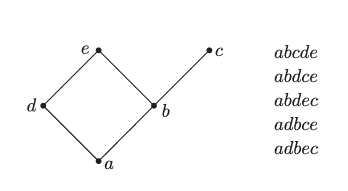
? (投票序列) nnn 位選民依次為候選人 A1,A2,…A_1, A_2, \ldotsA1?,A2?,… 投票的方式,使得對任意 iii,AiA_iAi? 獲得 λi\lambda_iλi? 票,且 AiA_iAi? 的得票數始終不低于 Ai+1A_{i+1}Ai+1?(記此類投票序列為 a1a2?ana_1 a_2 \cdots a_na1?a2??an?,其中第 kkk 位選民投票給 AakA_{a_k}Aak??)。
1112211212112211211212121
11122 \quad 11212 \quad 11221 \quad 12112 \quad 12121
1112211212112211211212121
(d) (格排列) 序列 a1a2?ana_1 a_2 \cdots a_na1?a2??an? 滿足:iii 出現 λi\lambda_iλi? 次,且對任意左因子 a1a2?aja_1 a_2 \cdots a_ja1?a2??aj?,iii 的出現次數不小于 i+1i+1i+1 的出現次數(對所有 iii)。此類序列稱為 λ\lambdaλ 型的格排列(或稱 Yamanouchi 詞或投票序列)。
1112211212112211211212121
11122 \quad 11212 \quad 11221 \quad 12112 \quad 12121
1112211212112211211212121
(e) (格路徑) R?\mathbb{R}^\ellR?(?=?(λ)\ell = \ell(\lambda)?=?(λ))中從原點 v0v_0v0? 到 vn=(λ1,λ2,…,λ?)v_n = (\lambda_1, \lambda_2, \ldots, \lambda_\ell)vn?=(λ1?,λ2?,…,λ??) 的格路徑 0=v0,v1,…,vn0 = v_0, v_1, \ldots, v_n0=v0?,v1?,…,vn?,每步為單位坐標向量,且保持在區域 x1≥x2≥?≥x?≥0x_1 \geq x_2 \geq \cdots \geq x_\ell \geq 0x1?≥x2?≥?≥x??≥0 內。

證明:
(a) 將 iii 插入到 λi?1\lambda^{i-1}λi?1 新增的方格中得到 λi\lambda^iλi,從而構造出形狀為 λ\lambdaλ 的標準楊表。
(b) Young 格 YYY 中的區間 [?,λ][\emptyset,\lambda][?,λ] 即為 J(Pλ)J(P_\lambda)J(Pλ?)(PλP_\lambdaPλ? 的序理想格),因此 fλf^\lambdafλ 的 (a) 和 (b) 兩種解釋的等價性實為命題 3.5.2 后續討論的特例。
? 若第 kkk 位投票者投票給 AiA_iAi?,則將 kkk 置于形狀 λ\lambdaλ 的第 iii 行。
(d) 顯然 ? 中的投票序列與 (d) 中的格排列完全相同。
(e) 若 a1a2?ana_1a_2\cdots a_na1?a2??an? 是 (d) 中的格排列,令 vi?vi?1v_i-v_{i-1}vi??vi?1? 為第 aia_iai? 個單位坐標向量(即第 aia_iai? 位為 1 其余為 0 的向量)可得到格路徑。或者,(b) 與 (e) 的等價性是例 3.5.3 前討論的特例。
上述五種解釋均可直接推廣至斜情形 fλ/μf^{\lambda/\mu}fλ/μ。具體細節留給感興趣的讀者。
在處理舒爾函數、Kostka數等問題時,有時使用行和列遞減的數組比半標準楊表(SSYT)更為方便。定義形狀為λ/μ\lambda/\muλ/μ的反向半標準楊表(reverse SSYT)或列嚴格平面劃分(簡稱costripp)為一個正整數數組,其形狀為λ/μ\lambda/\muλ/μ,滿足行弱遞減且列嚴格遞減。反向半標準楊表的類型α\alphaα的定義與普通半標準楊表相同。例如:
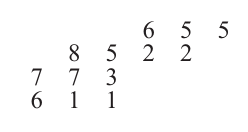
這是一個形狀為(6,5,3,3)/(3,1)(6,5,3,3)/(3,1)(6,5,3,3)/(3,1)、類型為(2,2,1,0,3,2,2,1)(2,2,1,0,3,2,2,1)(2,2,1,0,3,2,2,1)的反向半標準楊表。
值得提及一種與半標準楊表等價的組合對象。Gelfand-Tsetlin模式(有時簡稱為Gelfand模式)或完全分支是一個非負整數的三角數組GGG,形如:
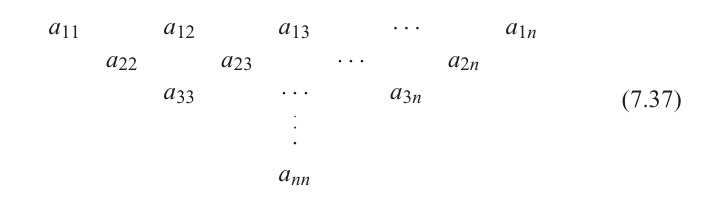
滿足當所有三個數都有定義時,aij≤ai+1,j+1≤ai,j+1a_{ij} \leq a_{i+1,j+1} \leq a_{i,j+1}aij?≤ai+1,j+1?≤ai,j+1?。換言之,GGG的行是弱遞增的,且ai+1,j+1a_{i+1,j+1}ai+1,j+1?位于其上方兩個相鄰數之間(含端點)。例如:

給定(7.37)式的Gelfand-Tsetlin模式GGG,令λi\lambda^iλi為GGG的第iii行逆序排列。通過將n?i+1n-i+1n?i+1插入斜形狀λi/λi+1\lambda^i/\lambda^{i+1}λi/λi+1的方格中,定義表格T=T(G)T=T(G)T=T(G)。對于上述例子,T(G)T(G)T(G)為:
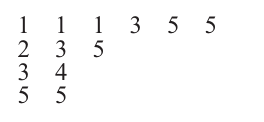
我們得到一個形狀為λ1\lambda^1λ1(GGG的第一行逆序)、最大部分不超過nnn的半標準楊表。這種具有固定第一行α\alphaα(長度為nnn)的Gelfand-Tsetlin模式與形狀為α′\alpha'α′(α\alphaα的逆序)、最大部分不超過nnn的半標準楊表之間的對應關系,顯然是一個雙射。
定義K^λ/μ,α\hat{K}_{\lambda/\mu,\alpha}K^λ/μ,α?為形狀λ/μ\lambda/\muλ/μ、類型α\alphaα的反向半標準楊表的數量。下一個命題表明,在許多情況下,普通半標準楊表與反向半標準楊表并無本質區別。
7.10.4 命題
設 λ/μ\lambda/\muλ/μ 為 nnn 的斜分劃,α\alphaα 為 nnn 的弱組合。則 K^λ/μ,α=Kλ/μ,α\hat{K}_{\lambda/\mu,\alpha} = K_{\lambda/\mu,\alpha}K^λ/μ,α?=Kλ/μ,α?。
證明:設 TTT 為形狀 λ/μ\lambda/\muλ/μ、類型 α=(α1,α2,…)\alpha=(\alpha_1,\alpha_2,\ldots)α=(α1?,α2?,…) 的反向半標準楊表,kkk 為 TTT 的最大部分。變換 Tij?k+1?TijT_{ij} \mapsto k+1-T_{ij}Tij??k+1?Tij? 表明 K^λ/μ,α=Kλ/μ,α\hat{K}_{\lambda/\mu,\alpha} = K_{\lambda/\mu,\alpha}K^λ/μ,α?=Kλ/μ,α?,其中 α=(αk,αk?1,…,α1,0,0,…)\alpha=(\alpha_k,\alpha_{k-1},\ldots,\alpha_1,0,0,\ldots)α=(αk?,αk?1?,…,α1?,0,0,…)。由定理 7.10.2 知 Kλ/μ,α=Kλ/μ,αK_{\lambda/\mu,\alpha} = K_{\lambda/\mu,\alpha}Kλ/μ,α?=Kλ/μ,α?,證畢。
7.10.5 命題
設 μ\muμ 和 λ\lambdaλ 為滿足 ∣μ∣=∣λ∣|\mu|=|\lambda|∣μ∣=∣λ∣ 且 Kλμ≠0K_{\lambda\mu}\neq 0Kλμ?=0 的分劃。則 μ≤λ\mu \leq \lambdaμ≤λ(支配序),且 Kλλ=1K_{\lambda\lambda}=1Kλλ?=1。
證明:若 Kλμ≠0K_{\lambda\mu} \neq 0Kλμ?=0,則存在形狀 λ\lambdaλ、類型 μ\muμ 的半標準楊表 TTT。假設某元素 Tij=kT_{ij}=kTij?=k 出現在第 kkk 行下方(即 i>ki>ki>k),則對 i>ki>ki>k 有 1≤T1k<T2k<?<Tik=k1 \leq T_{1k} < T_{2k} < \cdots < T_{ik}=k1≤T1k?<T2k?<?<Tik?=k,矛盾。故部分 1,2,…,k1,2,\ldots,k1,2,…,k 均在前 kkk 行出現,因此 μ1+μ2+?+μk≤λ1+λ2+?+λk\mu_1+\mu_2+\cdots+\mu_k \leq \lambda_1+\lambda_2+\cdots+\lambda_kμ1?+μ2?+?+μk?≤λ1?+λ2?+?+λk?。當 μ=λ\mu=\lambdaμ=λ 時必有 Tij=iT_{ij}=iTij?=i(對所有 (i,j)(i,j)(i,j)),故 Kλλ=1K_{\lambda\lambda}=1Kλλ?=1。
7.10.6 推論
舒爾函數 {sλ:λ∈Par(n)}\{s_\lambda : \lambda \in \text{Par}(n)\}{sλ?:λ∈Par(n)} 構成 Λn\Lambda^nΛn 的基,從而 {sλ:λ∈Par}\{s_\lambda : \lambda \in \text{Par}\}{sλ?:λ∈Par} 是 Λ\LambdaΛ 的基。事實上,對于任意擴張支配序的 Par(n)\text{Par}(n)Par(n) 線性序,表達 sλs_\lambdasλ? 關于 mμm_\mumμ? 的轉移矩陣 (Kλμ)(K_{\lambda\mu})(Kλμ?) 是主對角線為 1 的下三角矩陣。
證明:命題 7.10.5 等價于關于 (Kλμ)(K_{\lambda\mu})(Kλμ?) 的斷言。因主對角線為 1 的下三角矩陣可逆,故 {sλ}\{s_\lambda\}{sλ?} 是 Λn\Lambda^nΛn 的 Q\mathbb{Q}Q-基。
注:實際上 {sλ}\{s_\lambda\}{sλ?} 也是 ΛZn\Lambda^n_{\mathbb{Z}}ΛZn? 的 Z\mathbb{Z}Z-基,因每個 Kλλ=1K_{\lambda\lambda}=1Kλλ?=1(而非僅 Kλλ≠0K_{\lambda\lambda}\neq 0Kλλ?=0)。
后續章節將建立舒爾函數的基礎理論,包括:
- sλs_\lambdasλ? 與基 mλm_\lambdamλ?, hλh_\lambdahλ?, eλe_\lambdaeλ?, pλp_\lambdapλ? 間的轉移矩陣
- 與內積 ?,?\langle , \rangle?,? 及自同構 ω\omegaω 的聯系
(雖已通過定義考察 (Kλμ)(K_{\lambda\mu})(Kλμ?),但尚未知逆矩陣形式) - 對稱函數理論的計數應用:
- 平面劃分的枚舉
- 置換統計量的結果
- Polya 群作用計數理論
下表為 Kostka 數 KλμK_{\lambda\mu}Kλμ? 的簡表。


![[echarts]多個柱狀圖及圖例](http://pic.xiahunao.cn/[echarts]多個柱狀圖及圖例)





)








與流線程(Stream Threads)的協同設計)


