---

題目鏈接：

433. 最小基因變化

---

題目描述：

---

解法

先看懂題目

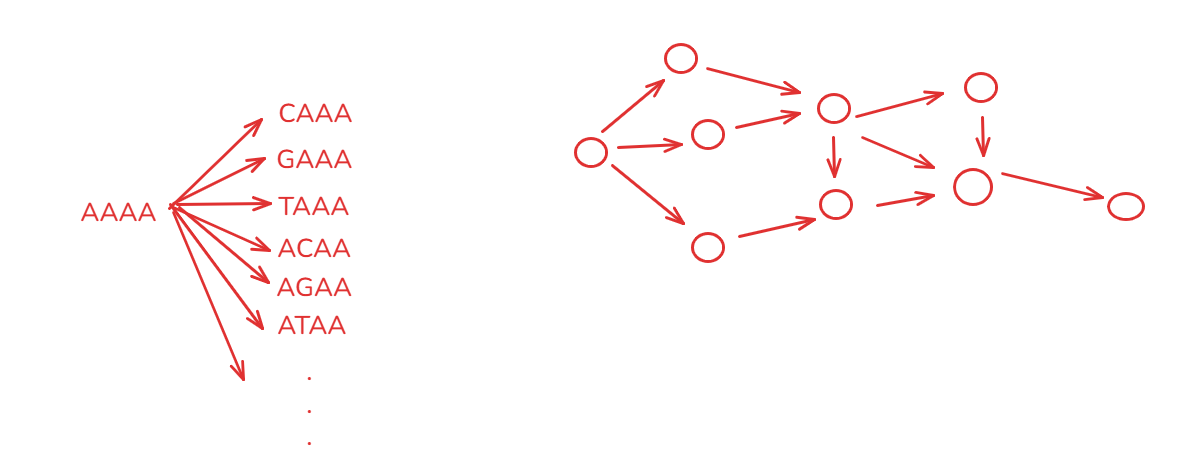
先把這個問題轉化：圖論問題

邊權為1的最短路問題。

為什么可以這么想？！

因為每次一步，最終目標也有。

---

C++ 算法代碼：

class Solution {
public:int minMutation(string startGene, string endGene, vector<string>& bank) {// 使用哈希集合存儲已訪問的基因序列unordered_set<string> vis; // 將基因庫轉換為哈希集合，方便快速查找unordered_set<string> hash(bank.begin(), bank.end()); // 可能的基因變化字符string change = "ACGT"; // 如果起始基因和目標基因相同，直接返回0if (startGene == endGene)return 0;// 如果目標基因不在基因庫中，直接返回-1if (!hash.count(endGene))return -1;// 使用BFS隊列queue<string> q;q.push(startGene);vis.insert(startGene);int ret = 0;  // 記錄突變次數while (q.size()) {ret++;  // 每處理完一層，突變次數加1int sz = q.size();  // 當前層的節點數// 處理當前層的所有節點while (sz--) {string t = q.front();q.pop();// 嘗試改變每個位置的字符for (int i = 0; i < 8; i++) {string tmp = t;  // 創建臨時副本，避免修改原字符串// 嘗試將當前位置的字符變為A/C/G/Tfor (int j = 0; j < 4; j++) {tmp[i] = change[j];// 如果變化后的序列在基因庫中且未被訪問過if (hash.count(tmp) && !vis.count(tmp)) {// 找到目標基因，返回當前突變次數if (tmp == endGene)return ret;// 將新序列加入隊列，并標記為已訪問q.push(tmp);vis.insert(tmp);}}}}}// 如果隊列為空仍未找到目標基因，返回-1return -1;}
};