一、核心概念與性質對比

1. B樹（Balanced Tree）

• 定位：多路平衡搜索樹，專為磁盤存儲優化

• 核心性質：

  • 每個節點存儲?k-1個鍵值和k個子節點指針（m/2 ≤ k ≤ m，m為階數）

  • 所有葉子節點位于同一層（高度平衡）

  • 節點內鍵值有序排列，左子樹鍵值均小于父節點，右子樹大于父節點

• 優勢：

  • 減少磁盤I/O：單節點存儲大量鍵值，樹高顯著降低（3-4層可存百萬數據）

  • 局部修改：插入/刪除僅影響局部節點，避免全局調整1

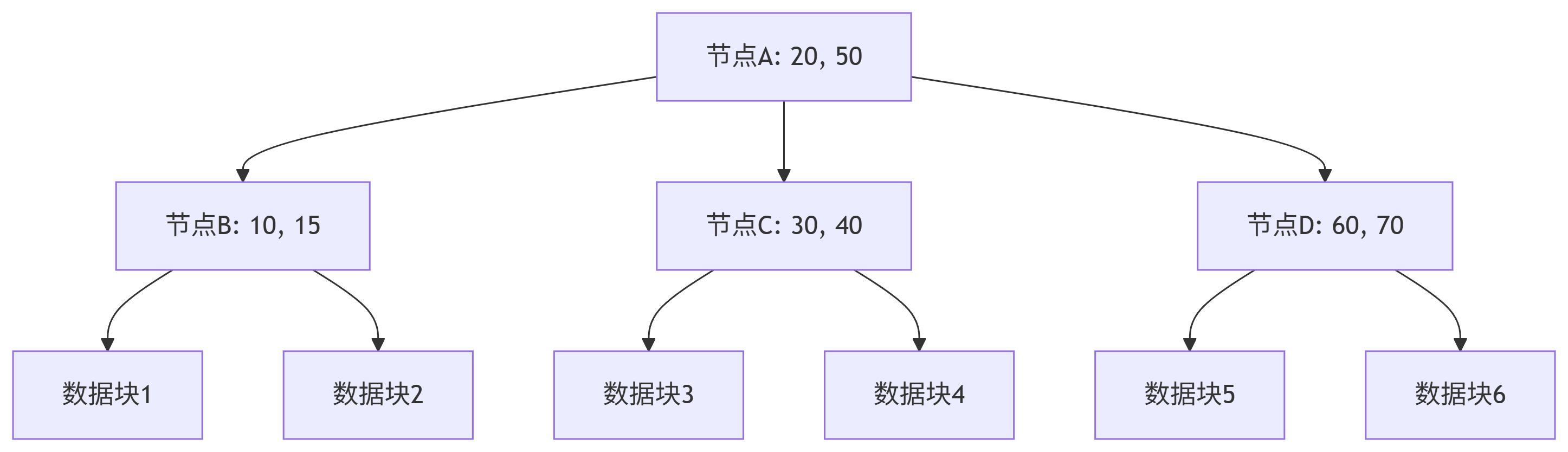
2. B+樹（B+ Tree）

• 定位：B樹變種，數據庫索引標準結構

• 核心性質：

  • 非葉節點僅存鍵值（無數據指針），葉節點存數據并形成雙向鏈表

  • 非葉節點的鍵值在葉節點中重復出現（葉節點含所有數據）

• 優勢：

  • 范圍查詢高效：葉節點鏈表支持順序遍歷（如SQL的BETWEEN）

  • 磁盤利用率更高：非葉節點容納更多鍵值，進一步降低樹高

  • 查詢穩定性：所有查詢路徑長度相同（均到葉節點）

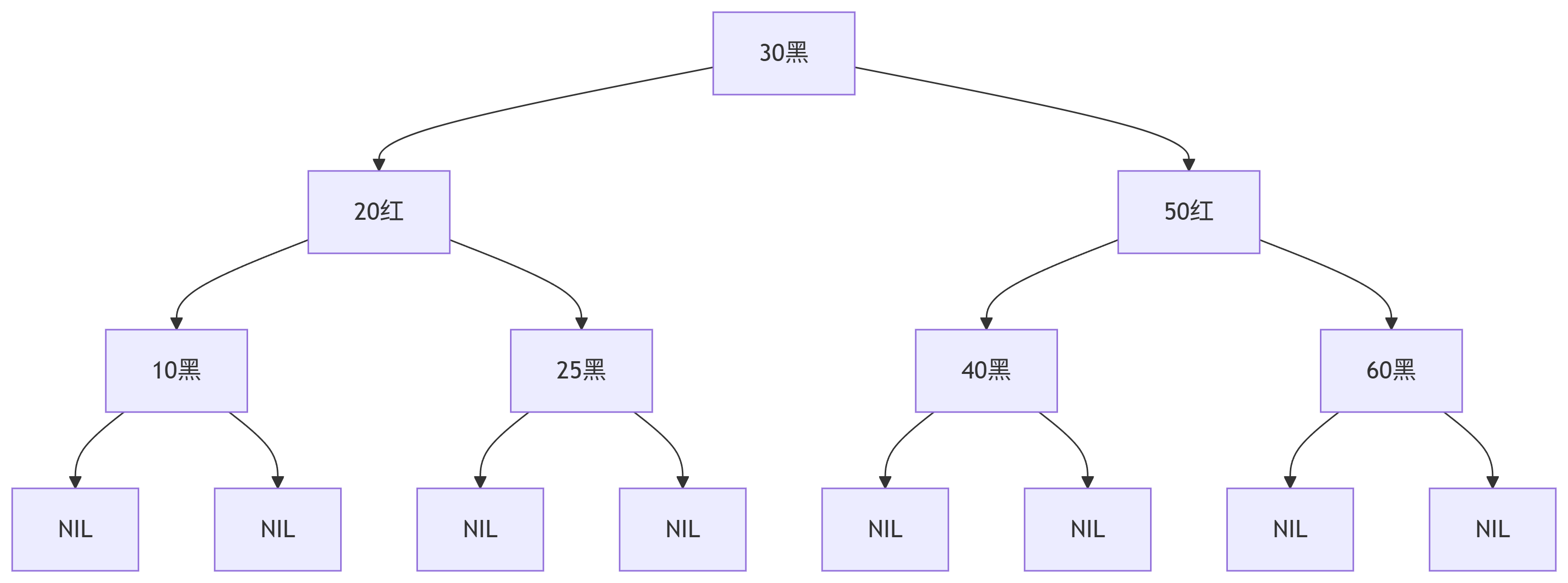
3. 紅黑樹（Red-Black Tree）

• 定位：自平衡二叉搜索樹，內存操作優化

• 核心性質：

  • 顏色約束：節點紅/黑交替，根和葉（NIL）為黑，無連續紅節點

  • 黑高平衡：任意節點到葉節點的路徑含相同黑節點數

• 優勢：

  • 近似平衡：最長路徑≤2倍最短路徑，保證O(log n)操作

  • 低維護成本：插入/刪除最多3次旋轉（遠少于AVL樹）

4. 三樹對比總結

特性	B樹	B+樹	紅黑樹
結構	多叉，數據存所有節點	多叉，數據僅存葉子	二叉，顏色標記平衡
樹高	極低（3-4層百萬級）	更低（同數據量更矮）	較高（約2logN）
磁盤I/O優化	優秀	最優（索引更緊湊）	無
范圍查詢	需中序遍歷	葉子鏈表直接遍歷	需中序遍歷
典型應用	文件系統	MySQL索引	Java TreeMap

---

二、操作復雜度與設計邏輯

1.?B/B+樹：

• 減少I/O次數：

  • 節點大小 ≈ 磁盤頁（如4KB），單次I/O加載數百鍵值

  • 二叉查找樹需O(log n)次I/O，B樹僅需O(log_m n)（m為分支因子）

• 插入/刪除邏輯：

  • 節點分裂：鍵值超限 → 中位數提升至父節點，分裂兩子節點

  • 節點合并：鍵值不足 → 向兄弟節點借鍵或與父節點合并

2.?紅黑樹：

• 旋轉與變色策略：

  • 插入5種Case：如叔節點紅則變色；叔節點黑則旋轉（左旋/右旋）

  • 刪除7種Case：根據兄弟節點顏色調整（如兄弟紅則旋轉+變色）

• 平衡代價：

  • 查詢：O(log n)（常數比AVL大）

  • 插入/刪除：旋轉次數O(1)，優于AVL樹的O(log n)

---

三、應用場景解析

1.?B樹：文件系統

• 代表：NTFS、Ext4

• 原因：

  • 文件塊存儲分散，B樹局部修改特性減少磁盤寫入

  • 目錄結構需快速定位分散存儲的文件塊

2.?B+樹：數據庫索引

• 代表：MySQL InnoDB

• 原因：

  • 范圍查詢高效：WHERE id BETWEEN 100 AND 200 → 葉節點鏈表遍歷

  • 聚簇索引優化：葉節點直接存行數據，避免二次查找

3.?紅黑樹：內存數據結構

• 代表：Java TreeMap、C++ std::map

• 原因：

  • 插入/刪除頻繁（如HashMap沖突鏈轉樹）

  • 避免AVL樹嚴格平衡的高維護成本

---

四、常見問題總結

Q1：數據庫為什么用B+樹不用紅黑樹？

A：核心在于磁盤I/O優化和范圍查詢支持：

• I/O次數：紅黑樹樹高約2logN，百萬數據需20次I/O；B+樹樹高僅3-4層（節點存數百鍵）。

• 范圍查詢：B+樹葉節點鏈表直接遍歷；紅黑樹需中序遍歷（回溯棧易溢出）。

• 數據局部性：B+樹非葉節點純索引，單頁緩存更多鍵值，縮小查找范圍。

Q2：B樹和B+樹區別？

A：聚焦數據存儲位置與葉子結構：

• 數據存儲：B樹所有節點存數據；B+樹數據僅存葉子，非葉節點為索引。

• 葉子鏈接：B+樹葉節點雙向鏈表支持順序訪問；B樹葉節點獨立。

• 查詢穩定性：B樹查詢可能在非葉節點結束；B+樹必須到葉子（穩定O(log n)）。

Q3：紅黑樹如何保證平衡？

A：通過顏色約束與旋轉策略：

• 黑高平衡：任意路徑黑節點數相同，確保最長路徑≤2倍最短路徑。

• 旋轉Case：插入分5種情況（如叔節點紅則變色，黑則旋轉）；刪除分7種（兄弟節點顏色決定操作）。

• 低開銷：插入/刪除最多3次旋轉（AVL可能需O(log n)次）。