? ? ? ? 本篇我們將學習新的數據結構——二叉樹。
? ? ? ? 作者的個人gitee:樓田莉子 (riko-lou-tian) - Gitee.com
目錄
樹的概念
? ? ? ? 樹形結構
? ? ? ? 非樹形結構
樹的相關術語
樹的表示
樹在實際生活上的應用
二叉樹
? ? ? ? 慢二叉樹
????????完全二叉樹
二叉樹的儲存結構
? ? ? ? 二叉樹的存儲結構
????????順序結構
? ? ? ? 鏈式結構
堆的概念(順序結構二叉樹)
堆的模擬實現
????????堆的結構
? ?? ? 堆的初始化
? ? ? ? 堆的銷毀
? ? ? ? 堆的打印?
? ? ? ? 判斷堆是否為空?
? ? ? ? 堆的數據插入
? ? ? ? 交換函數
? ? ? ? 堆向上調整
? ? ? ? 堆向下調整?
????????數據刪除
? ? ? ? 堆排序
堆的Top-k問題
樹的概念
? ? ? ? 樹是一種非線性的數據結構。它由n(n>=0)個有限結點組成?個具有層次關系的集合。把它叫做樹是因為它看起來像?棵倒掛的樹,也就是說它是根朝上,?葉朝下的。
? ? ? ? 樹形結構
????????有?個特殊的結點,稱為根結點,根結點沒有前驅結點
????????除根結點外,其余結點被分成 M(M>0) 個互不相交的集合 T1、T2、……、Tm ,其中每?個集合Ti(1 <= i <= m) ?是?棵結構與樹類似的?樹。每棵?樹的根結點有且只有?個前驅,可以有 0 個或多個后繼。因此,樹是遞歸定義的。
? ? ? ? 具體表現如下:
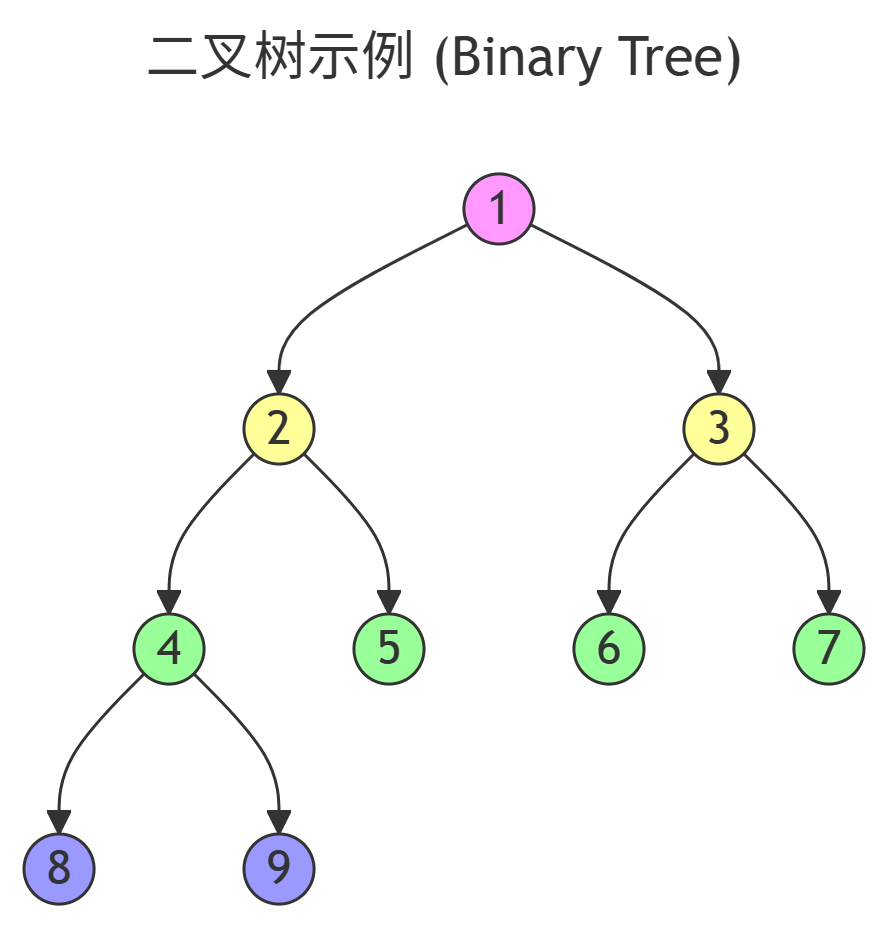
????????樹形結構中,?樹之間不能有交集,否則就不是樹形結構
? ? ? ? 當然實際上也存在非樹形結構。
? ? ? ? 非樹形結構
? ? ? ? 如下圖所示,就是幾個非樹形結構。
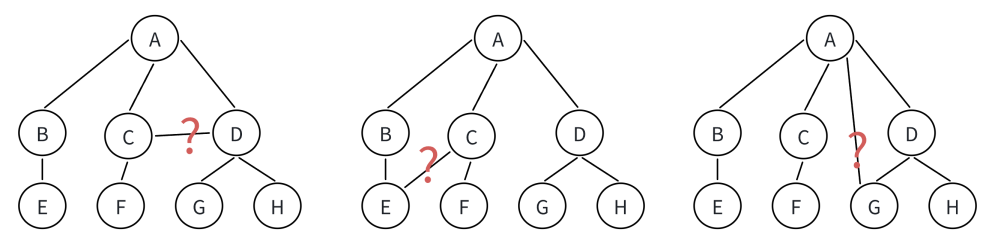
?????????樹是不相交的(如果存在相交就是圖)
????????除了根結點外,每個結點有且僅有?個?結點
?????????棵N個結點的樹有N-1條邊
樹的相關術語
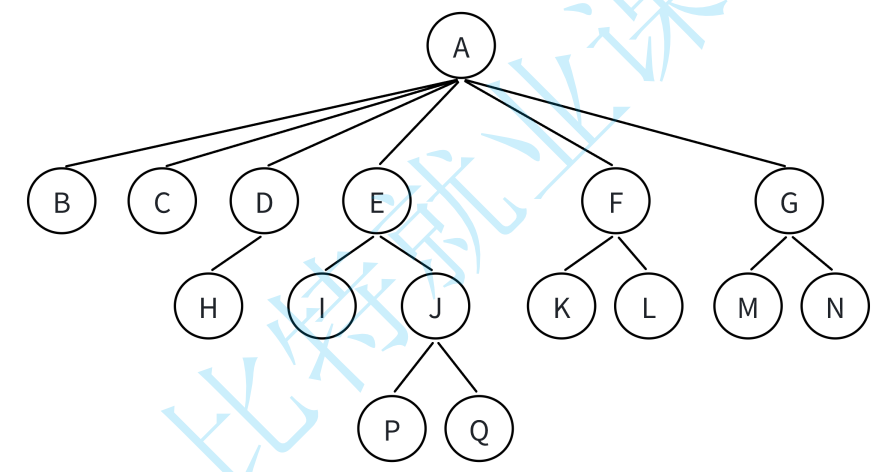
?結點/雙親結點:若?個結點含有?結點,則這個結點稱為其?結點的?結點; 如上圖:A是B的?結點
?結點/孩?結點:?個結點含有的?樹的根結點稱為該結點的?結點; 如上圖:B是A的孩?結點結點的度:?個結點有?個孩?,他的度就是多少;?如A的度為6,F的度為2,K的度為0
樹的度:?棵樹中,最?的結點的度稱為樹的度; 如上圖:樹的度為 6
葉?結點/終端結點:度為 0 的結點稱為葉結點; 如上圖: B、C、H、I... 等結點為葉結點 分?結點/?終端結點:度不為 0 的結點; 如上圖: D、E、F、G... 等結點為分?結點 兄弟結點:具有相同?結點的結點互稱為兄弟結點(親兄弟); 如上圖: B、C 是兄弟結點
結點的層次:從根開始定義起,根為第 1 層,根的?結點為第 2 層,以此類推;樹的?度或深度:樹中結點的最?層次; 如上圖:樹的?度為 4
結點的祖先:從根到該結點所經分?上的所有結點;如上圖: A 是所有結點的祖先
路徑:?條從樹中任意節點出發,沿?節點-?節點連接,達到任意節點的序列;?如A到Q的路徑為: A-E-J-Q;H到Q的路徑H-D-A-E-J-Q?孫:以某結點為根的?樹中任?結點都稱為該結點的?孫。如上圖:所有結點都是A的?孫
森林:由 m(m>0) 棵互不相交的樹的集合稱為森林;
樹的表示
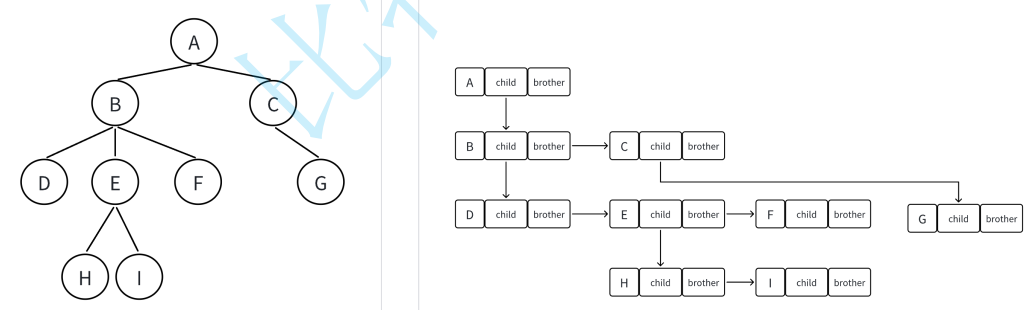
????????孩?兄弟表?法:
樹結構相對線性表就?較復雜了,要存儲表?起來就?較?煩了,既然保存值域,也要保存結點和結點之間的關系,實際中樹有很多種表??式如:雙親表?法,孩?表?法、孩?雙親表?法以及孩?兄弟表?法等。我們這?就簡單的了解其中最常?的孩?兄弟表?法
struct TreeNode
{
struct Node* child; // 左邊開始的第?個孩?結點
struct Node* brother; // 指向其右邊的下?個兄弟結點
int data; // 結點中的數據域
}????????由上述代碼,可以這么推廣
樹在實際生活上的應用
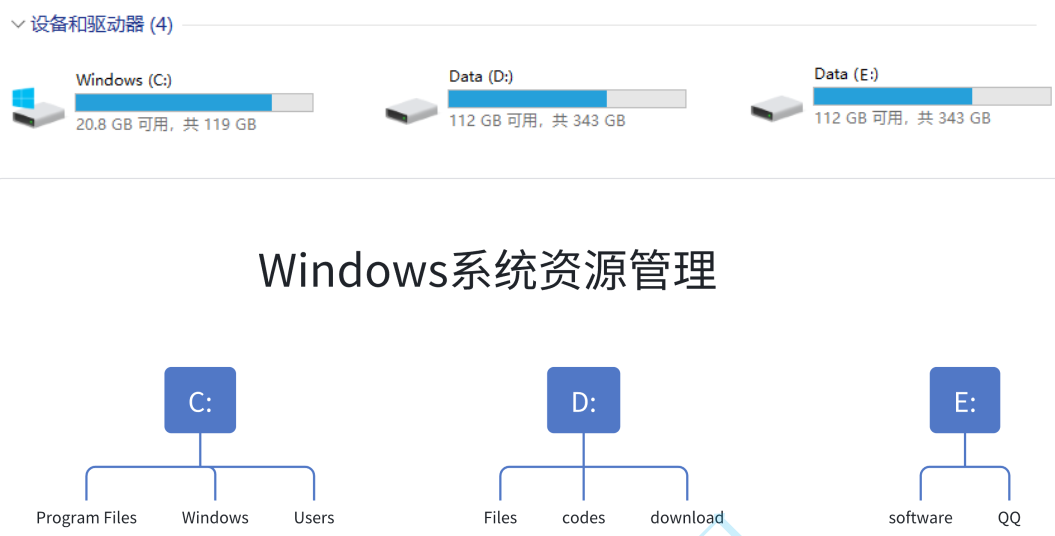
?????????件系統是計算機存儲和管理?件的?種?式,它利?樹形結構來組織和管理?件和?件夾。在?件系統中,樹結構被?泛應?,它通過?結點和?結點之間的關系來表?不同層級的?件和?件夾之間的關聯。
二叉樹
? ? ? ? 而樹型結構中,我們常用的是二叉樹。一棵二叉樹是結點的有限集合,該集合由?個根結點加上兩棵別稱為左?樹和右?樹的?叉樹組成或者為空。
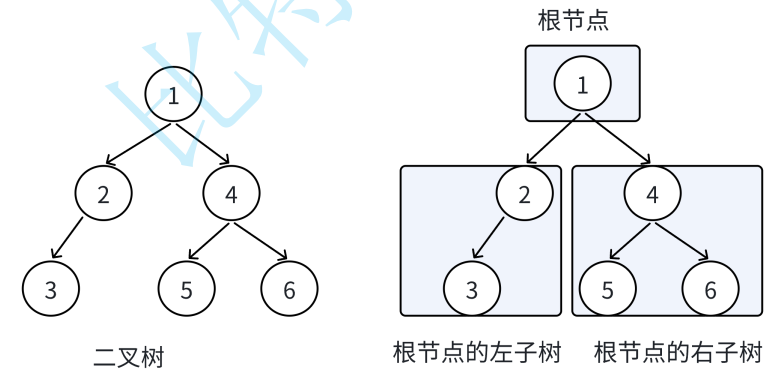
? ? ? ? 我們可以發現:
1. ?叉樹不存在度?于 2 的結點
2. ?叉樹的?樹有左右之分,次序不能顛倒,因此?叉樹是有序樹
注意:對于任意的?叉樹都是由以下?種情況復合?成的
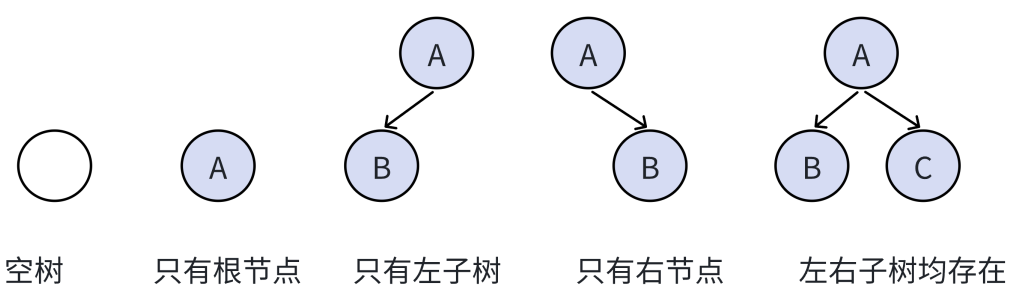
? ? ? ? 二叉樹也有特殊和普通兩種情況。
? ? ? ? 我們先學習特殊情況。
? ? ? ? 慢二叉樹
?????????個?叉樹,如果每?個層的結點數都達到最?值,則這個?叉樹就是滿?叉樹。也就是說,如果?個?叉樹的層數為 K ,且結點總數是 2k - 1 ,則它就是滿?叉樹。
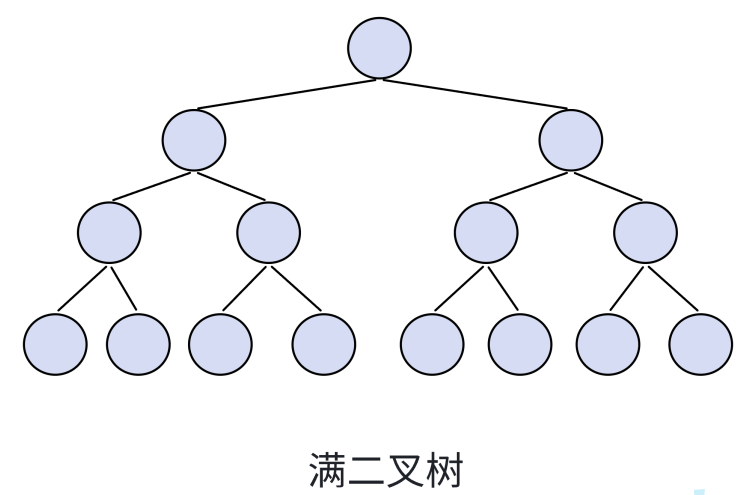
? ? ? ? 觀察發現滿二叉樹每一層有2^(n-1)個結點,則總結點數目就是2^n-1個(運用等比數列的求和公式)?
????????完全二叉樹
????????完全?叉樹是效率很?的數據結構,完全?叉樹是由滿?叉樹?引出來的。對于深度為 K 的,有 n 個結點的?叉樹,當且僅當其每?個結點都與深度為K的滿?叉樹中編號從 1 ? n 的結點??對應時稱之為完全?叉樹。要注意的是滿?叉樹是?種特殊的完全?叉樹
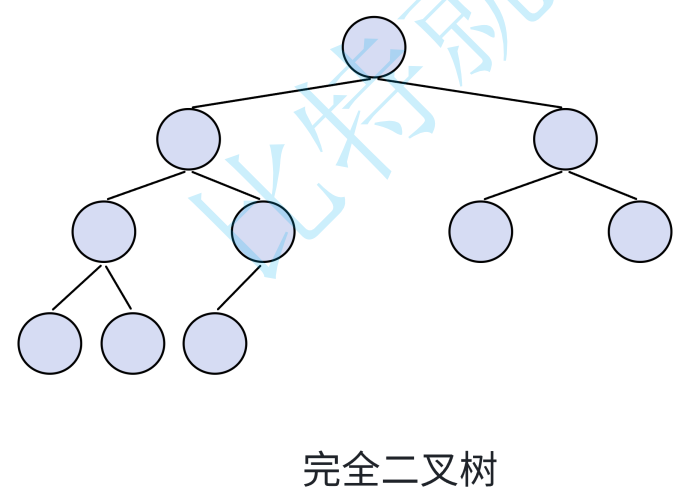
? ? ? ?完全二叉樹的特點:
????????(1)除了最后一層,每層節點個數達到最大。
? ? ? ? (2)最后一層的節點個數不一定達到最大。(最后一層達到最大則既是完全二叉樹也是滿二叉樹)
? ? ? ? (3)結點從左到右依次排列。
????????滿二叉樹一定是完全二叉樹,完全二叉樹不一定是滿二叉樹。
?叉樹性質
根據滿?叉樹的特點可知:
????????1、若規定根結點的層數為 1 ,則?棵?空?叉樹的第i層上最多有 2i-1 個結點
????????2、若規定根結點的層數為 1 ,則深度為 h 的?叉樹的最?結點數是 2h - 1
? ? ? ? 3、若規定根結點的層數為 1 ,具有 n 個結點的滿?叉樹的深度h= ( log以2為底, n+1 為對數)
二叉樹的儲存結構
? ? ? ? 二叉樹的存儲結構
?????????叉樹?般可以使?兩種結構存儲,?種順序結構,?種鏈式結構
????????順序結構
????????順序結構存儲就是使?數組來存儲,?般使?數組只適合表?完全?叉樹,因為不是完全?叉樹會有空間的浪費,完全?叉樹更適合使?順序結構存儲。
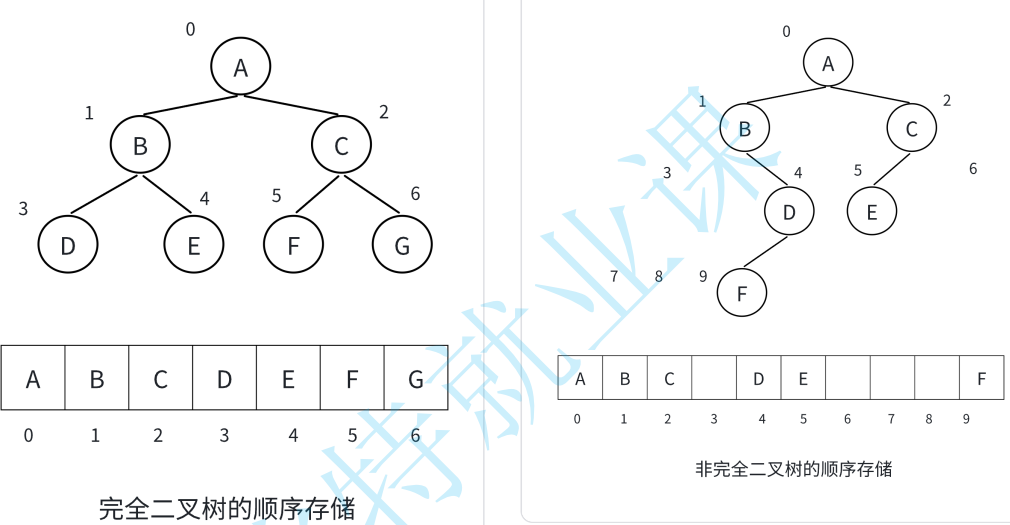
? ? ? ? 其中非完全二叉樹的空數組表示NULL。?
????????現實中我們通常把堆(?種?叉樹)使?順序結構的數組來存儲,需要注意的是這?的堆和操作系統虛擬進程地址空間中的堆是兩回事,?個是數據結構,?個是操作系統中管理內存的?塊區域分段。
? ? ? ? 鏈式結構
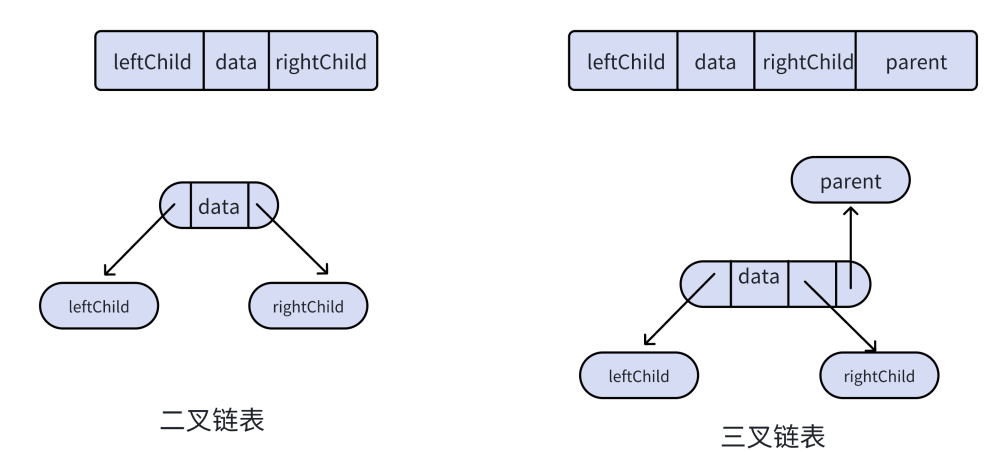
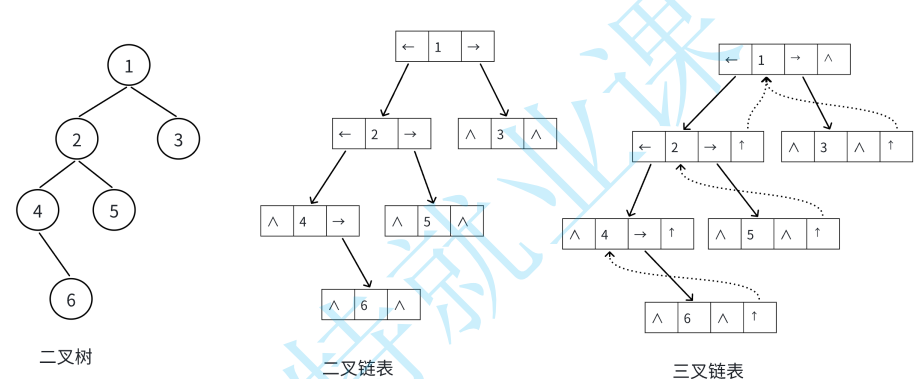
?????????叉樹的鏈式存儲結構是指,?鏈表來表??棵?叉樹,即?鏈來指?元素的邏輯關系。 通常的?法是鏈表中每個結點由三個域組成,數據域和左右指針域,左右指針分別?來給出該結點左孩?和右孩?所在的鏈結點的存儲地址 。鏈式結構?分為?叉鏈和三叉鏈,當前我們學習中?般都是?叉鏈。后期我們學到?階數據結構的時候如紅?樹等會?到三叉鏈。
堆的概念(順序結構二叉樹)
????????堆是一種特殊的二叉樹,除了二叉樹的性質之外還有其他的性質????????
????????如果有?個關鍵碼的集合 K = {k0 , k1 , k2 , ...,kn-1 },把它的所有元素按完全?叉樹的順序存儲?式存儲,在?個?維數組中,并滿?: Ki <= K2?i+1(Ki >= K2?i+1 且Ki <= K2?i+2),
i = 0、1、2... ,則稱為?堆(或?堆)。將根結點最?的堆叫做最?堆或?根堆,根結點最?的堆叫做最?堆或?根堆。
? ? ? ??堆分為兩類:
? ? ? ? 大根堆:
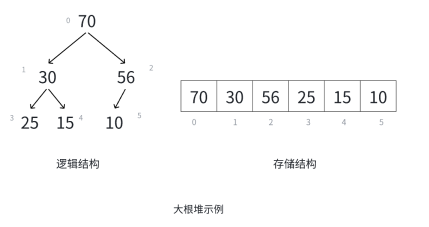
? ? ? ? 小根堆:
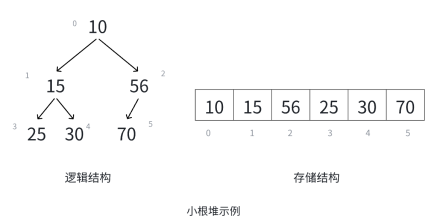
? ? ? 但是小堆≠升序,大堆≠降序。??
????????堆具有以下性質:
????????堆中某個結點的值總是不?于或不?于其?結點的值;
????????堆總是?棵完全?叉樹。
?????????叉樹性質:
對于具有 n 個結點的完全?叉樹,如果按照從上?下從左?右的數組順序對所有結點從
0 開始編號,則對于序號為 i 的結點有:
1. 若 i>0 , i 位置結點的雙親序號: (i-1)/2 ; i=0 , i 為根結點編號,?雙親結點
2. 若 2i+1<n ,左孩?序號: 2i+1 , 2i+1>=n 否則?左孩?。
3. 若 2i+2<n ,右孩?序號: 2i+2 , 2i+2>=n 否則?右孩?。
堆的模擬實現
????????堆的結構
typedef int HPDataType;
//堆的結構
typedef struct Heap
{HPDataType*arr; //堆中的數據int size; //堆的有效數據個數int capacity; //堆的總容量
}HP;
? ?? ? 堆的初始化
//堆的初始化
void HP_Init(HP* php)
{php->arr = NULL;php->size=php->capacity = 0;
}? ? ? ? 堆的銷毀
//堆的銷毀
void HP_Destroy(HP* php)
{if(php->arr)free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}? ? ? ? 堆的打印?
void HPPrint(HP* php)
{for (int i = 0; i < php->size; i++){printf("%d ", php->arr[i]);}printf("\n");
}? ? ? ? 判斷堆是否為空?
//判空
bool HP_Empty(HP* php)
{assert(php);return php->size == 0;
}? ? ? ? 堆的數據插入
? ? ? ? 初始版本:
//堆的插入操作
void HP_Push(HP* php, HPDataType data)
{assert(php->arr!= NULL);if (php->size == php->capacity){int new_capacity =php->capacity==0?4: (php->capacity) * 2;HPDataType*tmp=(HPDataType*)realloc(php->arr, new_capacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc error");exit(1);}php->arr = tmp;php->capacity = new_capacity;}php->arr[php->size++] = data;
}? ? ? ? 但是記住,數據插入后要進行調整讓它還是一個堆。
????????所以我們還需要一個堆向上調整的函數
? ? ? ? 因此?最終版本的數據插入函數
?//堆的插入操作
void HP_Push(HP* php, HPDataType data)
{assert(php);//判斷空間是否足夠if (php->size == php->capacity){int newCapcity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapcity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newCapcity;}php->arr[php->size] = data;//向上調整HP_UpAdjust(php->arr, php->size);++php->size;
}?? ? ? ? 交換函數
void swap(HPDataType* x, HPDataType* y)
{HPDataType tmp = *x;*x = *y;*y = tmp;
}? ? ? ? 堆向上調整
//堆在進行插入的時候需要調整為堆
//堆數據向上調整
void HP_UpAdjust(HPDataType* php, int child)
{int parent = (child - 1) / 2;while (child > 0){//大堆:>//小堆:<if (php[child] > php[parent]){//調整swap(&php[child], &php[parent]);child = parent;parent = (child - 1) / 2;}else {break;}}}? ? ? ? 堆向下調整?
//堆數據向下調整
void HP_DownAdjust(HPDataType* php, int parent,int n)
{int child =parent * 2 + 1;//左孩子while (child < n){//大堆:<//小堆:>if (child+1<n && php[child] < php[child + 1]){child++;}//大堆:>//小堆:<if (php[child] > php[parent]){//調整swap(&php[child], &php[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}? ? ? ? child循環了多少次取決于堆的高度/深度?
????????數據刪除
//堆的刪除操作
HPDataType HP_Pop(HP* php)
{assert(!HP_Empty(php));swap(&php->arr[0], &php->arr[php->size - 1]);--php->size;//向下調整HP_DownAdjust(php->arr, 0, php->size);
}? ? ? ? 堆排序
? ? ? ? 當我們寫出下面這行代碼的時候
void test2()
{HP hp;HP_Init(&hp);HP_Push(&hp, 27);HP_Push(&hp, 58);HP_Push(&hp, 10);HP_Push(&hp, 34);HPPrint(&hp);while (!HP_Empty(&hp)){int top=HP_Top(&hp);printf("%d ", top);HP_Pop(&hp);}HP_Destroy(&hp);
}? ? ? ? 運行一下結果為:
![]()
????????這就是堆排序嗎?
????????并不是。
? ? ? ? 在堆里堆頂一定是最值。大堆堆頂是最大值,小堆堆頂是最小值
? ? ? ? 堆的排序是利用堆的思想而不是利用堆的數據結構
? ? ? ? 在實際的堆排序中不可以用堆的數據結構來實現,最好用向下排序算法來構建堆的數據結構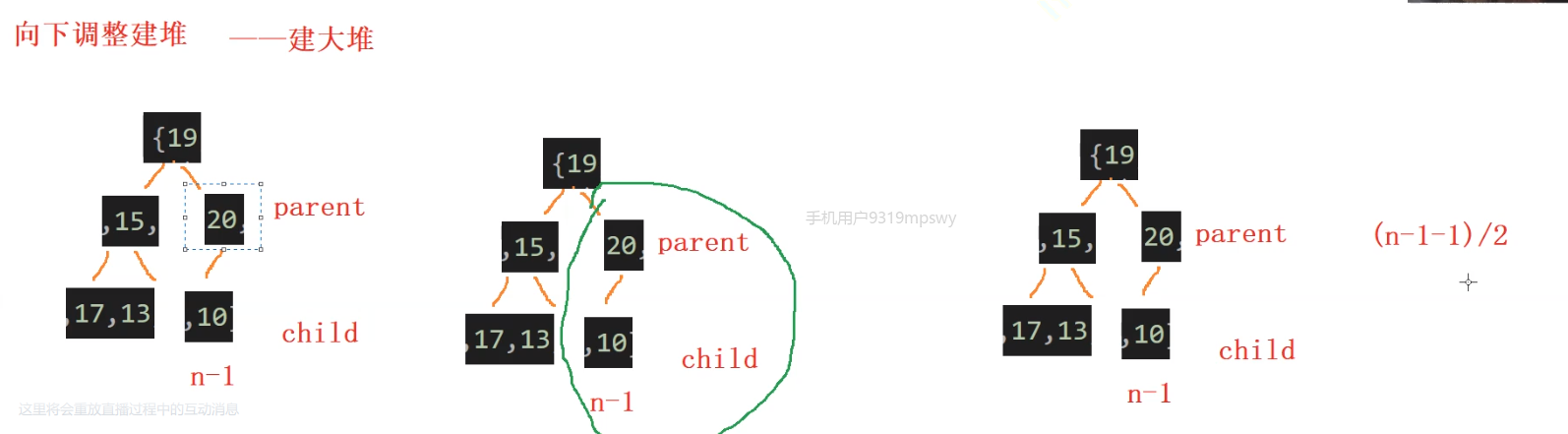
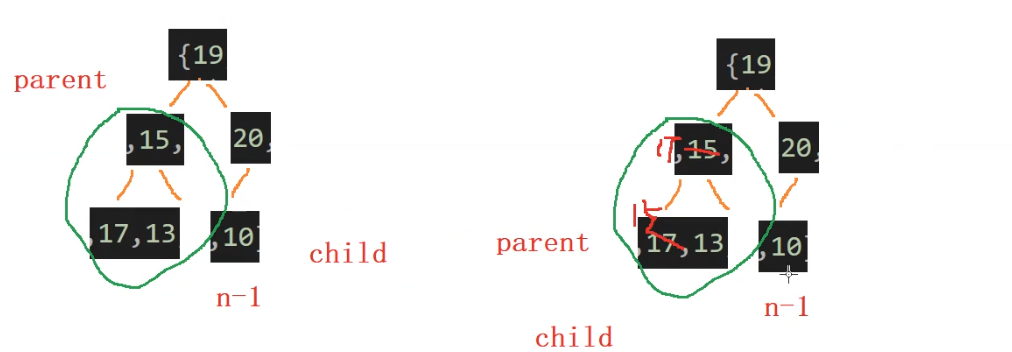
代碼如下:
向下調整算法的建堆:
//堆的堆排序操作
void HP_Sort(int* arr, int n)
{//建造堆——通過向下調整算法//n-1是最后一個子結點的下標,i表示的最后一個的父結點的下標for (int i =(n-1-1)/2; i >= 0; i--){HP_DownAdjust(arr, i, n);}//堆排序int end = n - 1;while (end > 0){//交換堆頂和最后一個元素swap(&arr[0], &arr[end]);//向下調整HP_DownAdjust(arr, 0, end);--end;}
}測試代碼:
void print(int *a,int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}
}
void test3()
{int a[] = { 58, 34, 27, 10, 91, 43, 61, 80, 12 };print(a,sizeof(a)/sizeof(a[0]));printf("\n");printf("排序后:\n");HP_Sort(a, 9);print(a, sizeof(a) / sizeof(a[0]));printf("\n");}向上調整算法建堆:
//堆的堆排序操作
void HP_Sort(int* arr, int n)
{//建造堆——通過向下調整算法//n-1是最后一個子結點的下標,i表示的最后一個的父結點的下標/*for (int i =(n-1-1)/2; i >= 0; i--){HP_DownAdjust(arr, i, n);}*///建堆——通過向上調整算法for (int i = 0;i < n;i++){HP_UpAdjust(arr, i, n);}//堆排序int end = n - 1;while (end > 0){//交換堆頂和最后一個元素swap(&arr[0], &arr[end]);//向下調整HP_DownAdjust(arr, 0, end);--end;}
}那么這兩者的時間復雜度有什么區別呢?
? ? ? ? 為了方便推理,我們使用滿二叉樹。因為堆是完全?叉樹,?滿?叉樹也是完全?叉樹,此處為了簡化使?滿?叉樹來證明(時間復雜度本來看的就是近似值,多?個結點不影響最終結果)
? ? ? ? 如下圖所示,
????????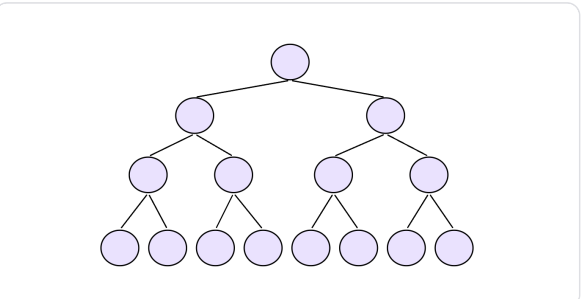
? ? ? ? 每一層有2^(n-1)個結點,需要向上移動n-1次,則需要移動結點總的移動步數為:每層結點個數 * 向上調整次數(第?層調整次數為0)
? ? ? ? 利用數列相關的求和知識可得:
? ? ? ? 由上可知,向上調整復雜度為O(N)
堆的Top-k問題
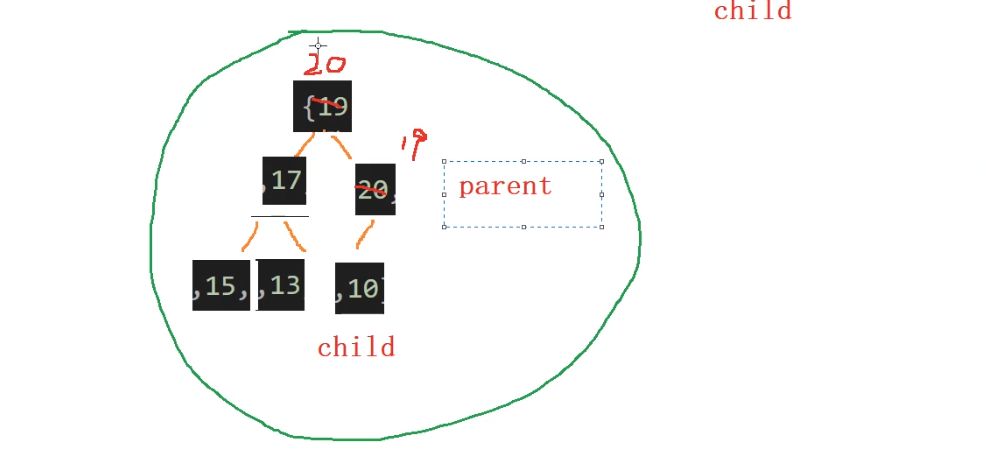
????????TOP-K問題:即求數據結合中前K個最?的元素或者最?的元素,?般情況下數據量都?較?。
?????????如:專業前10名、世界500強、富豪榜、游戲中前100的活躍玩家等。
????????對于Top-K問題,能想到的最簡單直接的?式就是排序,但是:如果數據量?常?,排序就不太可取了
(可能數據都不能?下?全部加載到內存中)。最佳的?式就是?堆來解決,基本思路如下:
????????1)?數據集合中前K個元素來建堆
????????前k個最?的元素,則建?堆
????????前k個最?的元素,則建?堆
????????2)?剩余的N-K個元素依次與堆頂元素來?較,不滿?則替換堆頂元素將剩余N-K個元素依次與堆頂元素?完之后,堆中剩余的K個元素就是所求的前K個最?或者最?的元素。
//top-k問題
//先建立一個數據
void createData()
{//創建數據int n = 10000;srand(time(0));const char* file = "data.txt";FILE* fp = fopen(file, "w");if (fp == NULL){printf("文件打開失敗!\n");return;}for (int i = 0; i < n; i++){int num = rand() % 10000;fprintf(fp, "%d\n", num);}fclose(fp);
}
void top_k()
{int k = 0;printf("請輸入k:>");scanf("%d", &k); const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");return;};int val = 0;int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc error");return;}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}// 建k個數據的小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){HP_DownAdjust(minheap, k, i);}// 遍歷剩下的n-k個數據int x = 0;while (fscanf(fout, "%d", &x) != EOF){// 如果當前值比堆頂大,替換堆頂并調整if (x > minheap[0]){minheap[0] = x;HP_DownAdjust(minheap, 0, k); }}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}printf("\n");//free(minheap); // 添加內存釋放fclose(fout);
}
//讀取數據
int main()
{top_k();return 0;
}? ? ? ? 時間復雜度分析:
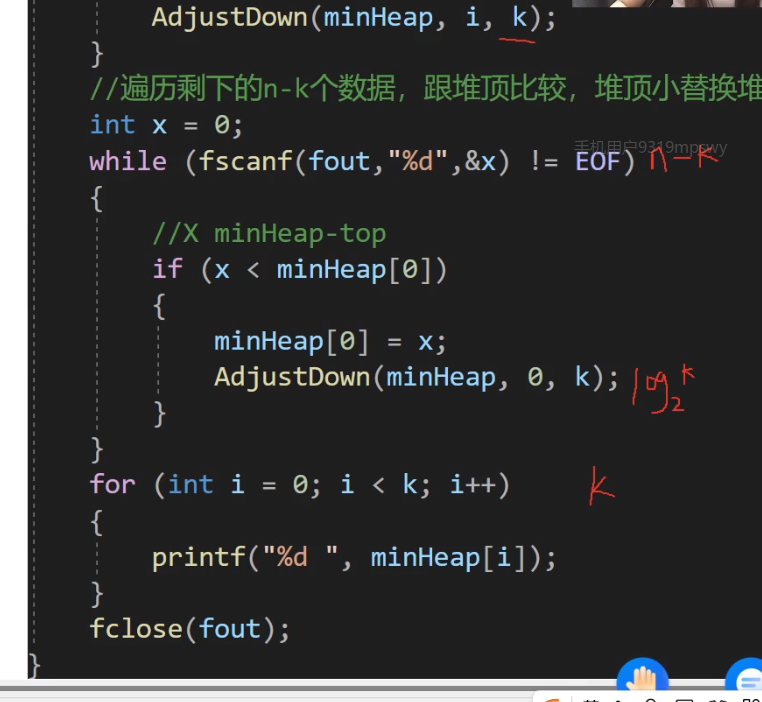
? ? ? ? 時間復雜度:O(n) = k + (n - k) log2 k
?
? ? ? ? 本期內容就到這里了,求一個點贊,謝謝
封面圖自取:







的解決方案)








)

--CompositionLocal)

