1. 集成學習：三個臭皮匠，如何賽過諸葛亮？

我們之前學習的線性回歸、決策樹等算法，就像是團隊里的某一位“專家”。這位專家可能在某個領域很擅長，但單憑他一人，要解決復雜多變的問題，總會遇到瓶頸。就好比，一位再厲害的“諸葛亮”，也難免有失算的時候。

那怎么辦呢？古人云：“三個臭皮匠，賽過諸葛亮”。**集成學習（Ensemble Learning）**的核心思想正是如此：它不依賴于某一個“超級天才”（強學習器），而是將一群“普通人”（弱學習器）的智慧匯集起來，形成一個決策能力超強的“專家團”（強學習器）。

一個弱學習器，通常指那些性能僅比隨機猜測好一點點的模型。而一個成功的“專家團”需要滿足兩個關鍵條件：

1. 個體優秀 (Good)：團隊里的每個成員（弱學習器）都得有兩把刷子，至少得具備一定的判斷能力（比如，分類準確率要大于50%）。
2. 彼此差異 (Different)：如果團隊成員的想法和知識背景一模一樣，那和一個人決策沒區別。成員之間必須有差異性、能互補短長，這樣集成的效果才會最好。

為了組建這樣的“專家團”，我們主要有兩種策略，可以從兩個維度來理解：

維度一：團隊成員的構成方式 (同質 vs. 異質)

• 異質集成 (Heterogeneous Ensemble)：這就像組建一個“跨學科團隊”。團隊里有搞數學的（線性回歸）、搞分類的（決策樹）、搞空間分析的（K近鄰）等等。我們讓每個不同類型的模型都對問題進行預測，然后給那些歷史表現更好的“專家”更高的發言權（權重），最后綜合所有人的加權意見，得出最終結論。
• 同質集成 (Homogeneous Ensemble)：這就像組建一個“專科攻堅小組”，所有成員都是同一類型，比如全是決策樹專家。為了避免大家想法一致，我們會給每個專家分發略有不同的“資料包”（攪動數據）。通過這種方式，即使模型類型相同，他們學到的側重點也各不相同，從而保證了差異性。

維度二：團隊的工作模式 (并行 vs. 串行)

• 并行集成 (Parallel Ensemble)：大家“同時開工，獨立思考”。就像一場開卷考試，我們給每個學生（弱學習器）發一份略有不同的復習資料（通過自助采樣得到的數據子集），讓他們獨立完成整套試卷。最后，我們統計所有學生的答案，通過“民主投票”來決定最終答案。這種方式互不干擾，非常適合大規模并行計算。

  • 代表算法：裝袋法 (Bagging)?和?隨機森林 (Random Forest)。

• 串行集成 (Serial Ensemble)：大家“接力工作，查漏補缺”。第一位同學（弱學習器）先做一遍題，然后把做錯的題目標記出來。第二位同學拿到后，就重點攻克上一位同學搞錯的難題。以此類推，每一位新成員都致力于解決前面所有成員留下的“歷史遺留問題”。這樣層層遞進，模型的能力越來越強。

  • 代表算法：提升法 (Boosting)，如 AdaBoost, GBDT, XGBoost 等。

分類維度	類型	核心思想	工作模式	代表算法	比喻
按構成	異質集成	不同類型的模型組合	各自預測，加權表決	Stacking	跨學科專家會診
	同質集成	同一類型的模型組合	通過數據擾動創造差異	Bagging, Boosting	決策樹專家小組
按生成	并行集成	獨立、互不依賴	同時訓練，投票/平均	Bagging, 隨機森林	學生獨立完成考試
	串行集成	依賴、層層遞進	迭代訓練，彌補前序錯誤	Boosting (AdaBoost, GBDT)	師徒接力解決難題

---

2. 隨機森林分類任務：民主投票的決策專家團

隨機森林是同質并行集成的杰出代表。顧名思義，“森林”由大量的“樹”（決策樹）組成。下面我們來看看這個“專家團”是如何工作的。

工作流程：

1. 建造森林：有控制的“隨機”

   • 樣本隨機 (Bootstrap Sampling)：假設我們有1000個原始樣本。為了訓練第一棵樹，我們從這1000個樣本中有放回地隨機抽取1000次，形成一個訓練集。因為是有放回的，所以這個新的訓練集中，有些樣本可能出現多次，有些則一次都未出現。這個過程就像是為每個專家準備一份獨特的“復習資料”。
   • 特征隨機 (Feature Sampling)：在決策樹的每個節點進行分裂時，我們不是從全部 P 個特征中尋找最優分裂點，而是隨機抽取 m 個特征（m < P），再從這 m 個中選出最好的。這確保了每棵樹都不會過分依賴某幾個強特征，增加了樹之間的“視角”差異。
     • 經驗法則：對于分類任務，通常取?m ≈ √p；對于回歸任務，取?m ≈ p/3。
     • 與裝袋法(Bagging)的關系：如果設置?m = p，即每次都考慮所有特征，那隨機森林就退化成了裝袋法。所以說，隨機森林是裝袋法的一種“進階版”，它通過增加特征隨機性來進一步提升模型的多樣性。

2. 獨立訓練：并行工作的專家
   每棵決策樹都使用自己獨特的樣本集和特征子集進行獨立訓練，互不干擾。

3. 集中決策：少數服從多數
   當一個新的樣本需要預測時，森林里的每一棵樹都獨立地給出一個自己的分類判斷。最后，隨機森林采用“多數投票 (Majority Voting)”原則，得票最多的那個類別就是最終的預測結果。

優點與缺點：

• 優點：
  • 高準確率與抗過擬合：通過平均/投票多棵樹的結果，個別樹的錯誤會被其他樹糾正，使得整體模型非常穩健，不易過擬含。
  • 處理高維數據：即使有數千個特征，隨機森林也能表現良好，并且能幫我們評估哪些特征更重要。
  • 易于并行化：各棵樹的訓練可以分散到多個CPU核心或機器上，效率很高。
• 缺點：
  • 可解釋性較差：相對于單棵決策樹，由成百上千棵樹組成的“黑箱”模型，我們很難直觀地理解其內部的決策邏輯。（這催生了下面要講的解釋性工具！）
  • 計算成本：對于大數據集，訓練大量的樹會消耗較多的時間和內存。

---

3. 誰是MVP？解密隨機森林的特征重要性

隨機森林是一個“黑箱”，但我們依然有辦法窺探其內部，比如，搞清楚“在所有決策中，哪個特征的貢獻最大？” 這就像評選一支球隊的“最有價值球員 (MVP)”。

核心思想：一個特征越重要，意味著它在分裂決策樹節點時，起到的“讓數據變純粹”的作用越大。

計算方法：

1. 單棵樹的貢獻：在一棵決策樹中，每當一個特征被用來分裂節點時，我們會計算這次分裂帶來的“不純度下降量”（例如，基尼指數下降或信息增益提升）。把這個特征在這棵樹里所有分裂點的貢獻加起來，就是它在這棵樹里的重要性得分。
2. 整個森林的總評：將該特征在森林中所有樹上的重要性得分進行平均，就得到了它在整個隨機森林中的最終重要性排名。

一句話總結：一個特征的重要性，就是它在所有樹中、所有分裂決策里，平均貢獻度的總和。貢獻越大，排名越靠前，它就是我們模型眼中的“MVP”。

---

4. 不止看“誰”重要，更要看“如何”重要：模型的可解釋性利器

特征重要性告訴我們“哪些”特征是MVP，但沒有告訴我們這個MVP“如何”影響比賽結果的（例如，是得分能力強還是防守能力強？）。部分依賴圖 (PDP)?和?個體條件期望圖 (ICE)?就是為了回答“如何影響”這個問題的強大工具。

1. 部分依賴圖 (Partial Dependence Plot, PDP)：看清“平均趨勢”

• 解決的問題：它展示了當其他所有特征保持不變時，某一個特征值的變化，對模型平均預測結果的影響。
• 比喻：就像研究“咖啡因攝入量”對“所有學生平均專注度”的影響。我們想知道，是咖啡因越多越好，還是適量最好？
• 工作原理：
  1. 選擇一個你感興趣的特征，比如“年齡”。
  2. 固定住數據集中其他所有特征，然后強制讓所有樣本的“年齡”都等于20歲，計算出所有樣本的平均預測概率。
  3. 接著，強制讓所有樣本的“年齡”都等于21歲，再算一個平均預測概率。
  4. …以此類推，將不同年齡值對應的平均預測結果連接起來，就形成了一條曲線。
• 解讀：這條曲線展示了“年齡”這個特征對模型預測結果的邊際效應。我們可以直觀地看到，隨著年齡的增長，預測結果是線性上升、下降，還是呈現更復雜的關系。

2. 個體條件期望圖 (Individual Conditional Expectation, ICE Plot)：洞察“個體故事”

• 解決的問題：PDP展示的是平均效果，但這種“平均”可能會掩蓋個體之間的巨大差異。ICE圖則為每一個樣本都畫出一條線，展示特定特征的變化對該樣本預測結果的影響。
• 比喻：PDP是看咖啡因對“所有學生”的平均影響，而ICE圖是看咖啡因對“張三”、“李四”每個人專注度的具體影響。可能張三喝了咖啡生龍活虎，李四喝了卻心慌意亂。
• 工作原理：它和PDP的原理幾乎一樣，唯一的區別是——它不對所有樣本的預測結果求平均。它為每個樣本單獨畫出一條“特征-預測”關系曲線。
• 解讀：
  • ICE圖是PDP的“拆解版”。所有ICE曲線的平均線，就是PDP曲線。
  • 通過觀察ICE圖，我們可以發現是否存在一些行為特異的子群體。如果所有ICE曲線都大致平行，說明該特征對所有樣本的影響是同質的。如果曲線雜亂無章，說明存在復雜的交互效應。

一句話總結：

• 特征重要性：告訴你哪個特征是MVP。
• PDP：告訴你這位MVP對**整個團隊（所有樣本）**的平均影響是怎樣的。
• ICE：告訴你這位MVP對**每一位隊員（單個樣本）**的具體影響是怎樣的。

數據13.1中的數據為例進行講解。針對“數據13.1”，我們以credit（是否發生違約）為響應變量，以age（年齡）、education（受教育程度）、workyears（工作年限）、resideyears（居住年限）、income（年收入水平）、debtratio（債務收入比）、creditdebt（信用卡負債）、otherdebt（其他負債）為特征變量，使用分類隨機森林算法進行。

5.隨機森林算法分類問題案例解析

1 ?變量設置及數據處理

from sklearn.ensemble import RandomForestClassifierfrom sklearn.ensemble import RandomForestRegressorfrom sklearn.metrics import confusion_matrixfrom sklearn.metrics import classification_reportfrom sklearn.metrics import cohen_kappa_scorefrom sklearn.inspection import PartialDependenceDisplayfrom mlxtend.plotting import plot_decision_regions#分類問題隨機森林算法示例#1  變量設置及數據處理data=pd.read_csv('數據13.1.csv')X = data.iloc[:,1:]#設置特征變量y = data.iloc[:,0]#設置響應變量X_train, X_test, y_train, y_test =  train_test_split(X,y,test_size=0.3, stratify=y, random_state=10)

2 ?二元Logistic回歸、單顆分類決策樹算法對比觀察

#2  二元Logistic回歸、單顆分類決策樹算法觀察model =  LogisticRegression(C=1e10, max_iter=1000,fit_intercept=True)model.fit(X_train, y_train)model.score(X_test, y_test)#單顆分類決策樹算法model = DecisionTreeClassifier()path = model.cost_complexity_pruning_path(X_train, y_train)param_grid = {'ccp_alpha': path.ccp_alphas}kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=10)model = GridSearchCV(DecisionTreeClassifier(random_state=10), param_grid, cv=kfold)model.fit(X_train, y_train)print("最優alpha值：", model.best_params_)     model = model.best_estimator_print("最優預測準確率：", model.score(X_test, y_test))

最優alpha值：{'ccp_alpha': 0.004534462760155709}

最優預測準確率：0.861904761904762

3 ?裝袋法分類算法

# 3  裝袋法分類算法model=BaggingClassifier(estimator=DecisionTreeClassifier(random_state=10),n_estimators=300,max_samples=0.8,random_state=0)model.fit(X_train, y_train)model.score(X_test, y_test)

0.8666666666666667

4 ?隨機森林分類算法

# 4  隨機森林分類算法model = RandomForestClassifier(n_estimators=300, max_features='sqrt', random_state=10)model.fit(X_train, y_train)model.score(X_test, y_test)

5 ?尋求max_features最優參數

#5  尋求max_features最優參數scores = []for max_features in range(1, X.shape[1] + 1):    model = RandomForestClassifier(max_features=max_features,                                  n_estimators=300, random_state=10)    model.fit(X_train, y_train)    score = model.score(X_test, y_test)    scores.append(score)index = np.argmax(scores)range(1, X.shape[1] + 1)[index]plt.rcParams['font.sans-serif']=['SimHei'] #正常顯示中文plt.plot(range(1, X.shape[1] + 1), scores, 'o-')plt.axvline(range(1, X.shape[1] + 1)[index], linestyle='--', color='k', linewidth=1)plt.xlabel('最大特征變量數')plt.ylabel('最優預測準確率')plt.title('預測準確率隨選取的最大特征變量數變化情況')plt.show()plt.savefig('預測準確率隨選取的最大特征變量數變化情況.png')print(scores)

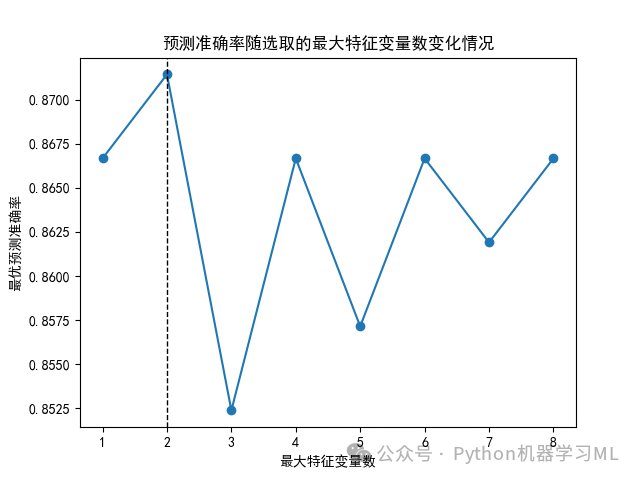
6 ?尋求n_estimators最優參數

#6  尋求n_estimators最優參數ScoreAll = []for i in range(100,300,10):    model= RandomForestClassifier(max_features=2,n_estimators = i,random_state = 10)    model.fit(X_train, y_train)    score = model.score(X_test, y_test)    ScoreAll.append([i,score])ScoreAll = np.array(ScoreAll)print(ScoreAll)max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] #找出最高得分對應的索引print("最優參數以及最高得分:",ScoreAll[max_score])  plt.rcParams['font.sans-serif']=['SimHei'] #正常顯示中文plt.figure(figsize=[20,5])plt.xlabel('n_estimators')plt.ylabel('預測準確率')plt.title('預測準確率隨n_estimators變化情況')plt.plot(ScoreAll[:,0],ScoreAll[:,1])plt.show()plt.savefig('預測準確率隨n_estimators變化情況.png')

進一步尋求n_estimators最優參數

#進一步尋求n_estimators最優參數ScoreAll = []for i in range(190,210):    model= RandomForestClassifier(max_features=2,n_estimators = i,random_state = 10)    model.fit(X_train, y_train)    score = model.score(X_test, y_test)    ScoreAll.append([i,score])ScoreAll = np.array(ScoreAll)print(ScoreAll)max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] #找出最高得分對應的索引print("最優參數以及最高得分:",ScoreAll[max_score])  plt.figure(figsize=[20,5])plt.xlabel('n_estimators')plt.ylabel('預測準確率')plt.title('預測準確率隨n_estimators變化情況')plt.plot(ScoreAll[:,0],ScoreAll[:,1])plt.show()plt.savefig('預測準確率隨n_estimators變化情況.png')

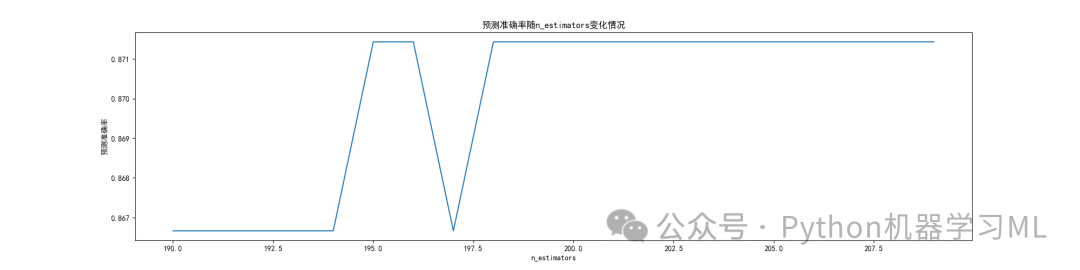
7 ?隨機森林特征變量重要性水平分析????

# 7  隨機森林特征變量重要性水平分析sorted_index = model.feature_importances_.argsort()plt.rcParams['font.sans-serif'] = ['SimHei']#解決圖表中中文顯示問題plt.barh(range(X_train.shape[1]), model.feature_importances_[sorted_index])plt.yticks(np.arange(X_train.shape[1]), X_train.columns[sorted_index])plt.xlabel('特征變量重要性水平')plt.ylabel('特征變量')plt.title('隨機森林特征變量重要性水平分析')plt.tight_layout()plt.show()plt.savefig('隨機森林特征變量重要性水平分析.png')

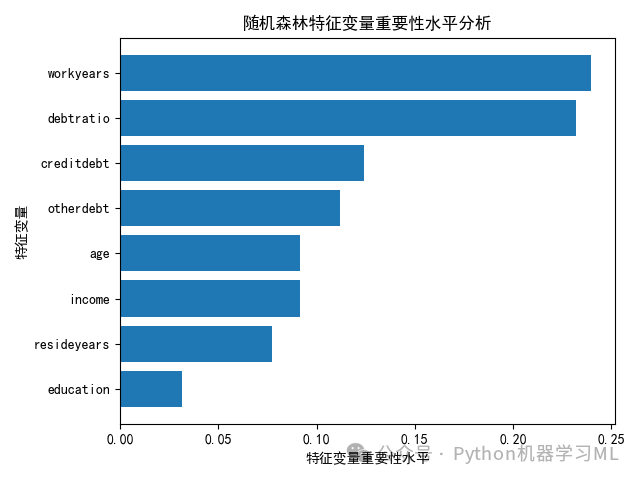
8 ?繪制部分依賴圖與個體條件期望圖???????

#8  繪制部分依賴圖與個體條件期望圖PartialDependenceDisplay.from_estimator(model, X_train, ['workyears','debtratio'], kind='average')#繪制部分依賴圖簡稱PDP圖PartialDependenceDisplay.from_estimator(model, X_train, ['workyears','debtratio'],kind='individual')#繪制個體條件期望圖（ICE Plot）PartialDependenceDisplay.from_estimator(model, X_train, ['workyears','debtratio'],kind='both')#繪制個體條件期望圖（ICE Plot）plt.show()plt.savefig('部分依賴圖與個體條件期望圖.png')

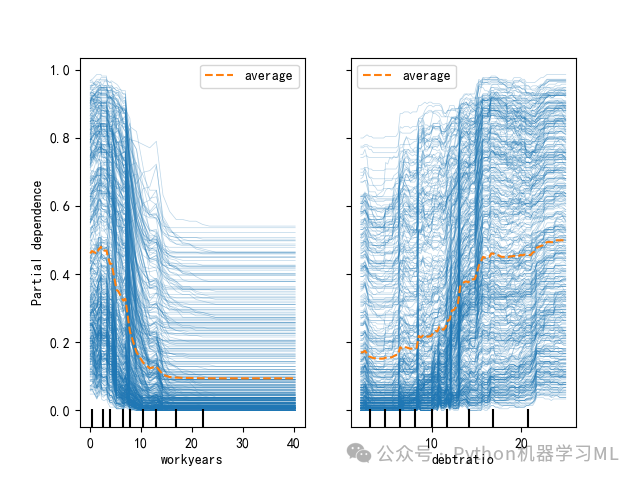
9 ?模型性能評價

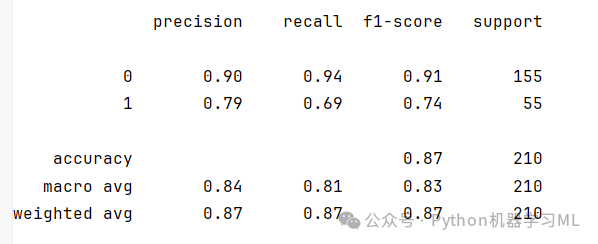
#9  模型性能評價prob = model.predict_proba(X_test)prob[:5]pred = model.predict(X_test)pred[:5]print(classification_report(y_test,pred))cohen_kappa_score(y_test, pred)#計算kappa得分

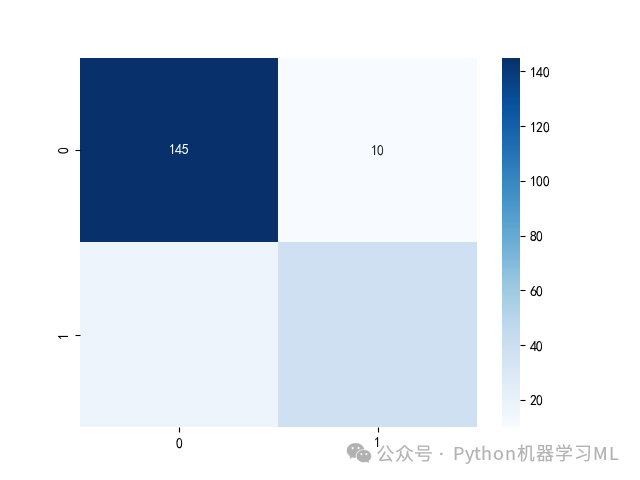
熱力圖

#熱力圖import seaborn as snssns.heatmap(confusion_matrix(y_test, pred), annot=True, fmt='d', cmap='Blues')plt.show()plt.savefig('混淆矩陣熱力圖.png')

10 ?繪制ROC曲線

???????

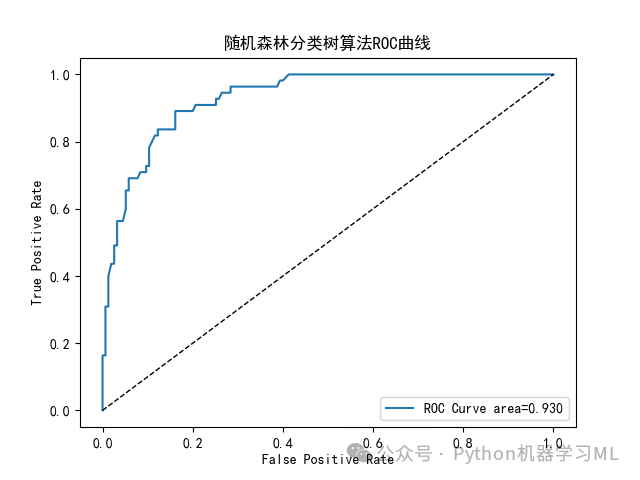
#10  繪制ROC曲線plt.rcParams['font.sans-serif'] = ['SimHei']#解決圖表中中文顯示問題from sklearn.metrics import roc_curve,roc_auc_score
# 假設 y_true 和 y_score 是你的真實標簽和模型預測的概率得分predict_target_prob=model.predict_proba(X_test)fpr, tpr, thresholds = roc_curve(y_test, predict_target_prob[:,1])# 計算AUC值auc = roc_auc_score(y_test, predict_target_prob[:,1])print("AUC值：", auc)# 繪制 ROC 曲線plt.plot(fpr, tpr, label='ROC Curve area=%.3f'%auc)plt.plot(fpr, fpr, 'k--', linewidth=1)plt.xlabel('False Positive Rate')plt.ylabel('True Positive Rate')plt.title('隨機森林分類樹算法ROC曲線')plt.legend()plt.show()plt.savefig('隨機森林分類樹算法ROC曲線.pdf')

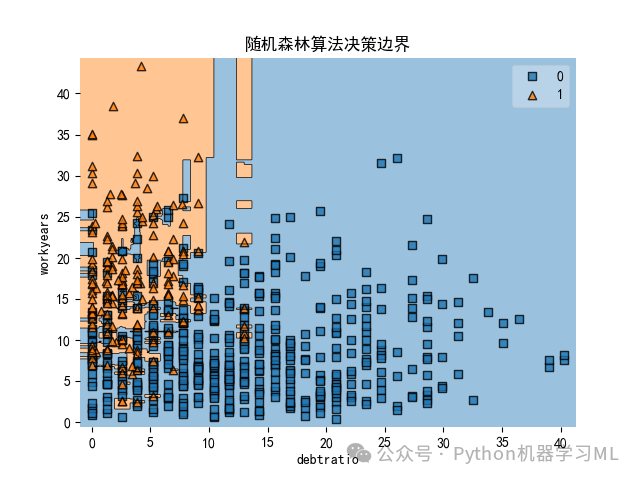
11 ?運用兩個特征變量繪制隨機森林算法決策邊界圖

#11  運用兩個特征變量繪制隨機森林算法決策邊界圖X2 = X.iloc[:, [2,5]]#僅選取workyears、debtratio作為特征變量model = RandomForestClassifier(n_estimators=300, max_features=1, random_state=1)model.fit(X2,y)model.score(X2,y)plot_decision_regions(np.array(X2), np.array(y), model)plt.xlabel('debtratio')#將x軸設置為'debtratio'plt.ylabel('workyears')#將y軸設置為'workyears'plt.title('隨機森林算法決策邊界')#將標題設置為'隨機森林算法決策邊界'plt.show()plt.savefig('隨機森林算法決策邊界.png')