排序與選擇
算法排序分類
- 基于比較的排序算法:
- 交換排序
- 冒泡排序
- 快速排序
- 插入排序
- 直接插入排序
- 二分插入排序
- Shell排序
- 選擇排序
- 簡單選擇排序
- 堆排序
- 合并排序
- 基于數字和地址計算的排序方法
- 計數排序
- 桶排序
- 基數排序
?簡單排序算法
????????冒泡排序
void sort(Item a[],int l,int r) {for(int i=l+1;i<=r;i++){for(int j=i;j>1;j++){compswap(a[j-1],a[j]);}} }
上述冒泡排序中,待排序元素類型是Item,算法根據Item類型元素的鍵值對數組元素a[l]~a[r]進行排序。算法中用到關于Item類型變量的一些常用運算:
typedef int Item; //待排序元素類型 typedef Item* addr;#define key(A) A #define less(A,B) (key(A)<key(B)) #define eq(A,B) (!less(A,B) && !less(B,A)) #define swap(A,B) {Item t=A;A=B;B=t;} #define compswap(A,B) if(less(B,A))swap(A,B)void ItemShow(Item x) {printf("%d \n",x); }其中,less(A,B)比較A和B的鍵值,等價于key(A)<key(B);
eq(A,B)等價于key(A)==key(B);
swap(A,B)交換兩個元素的值;
compswap(A,B)等價于語句if(less(A,B)) swap(A,B),即當key(B)<key(A)時,交換A和B的值
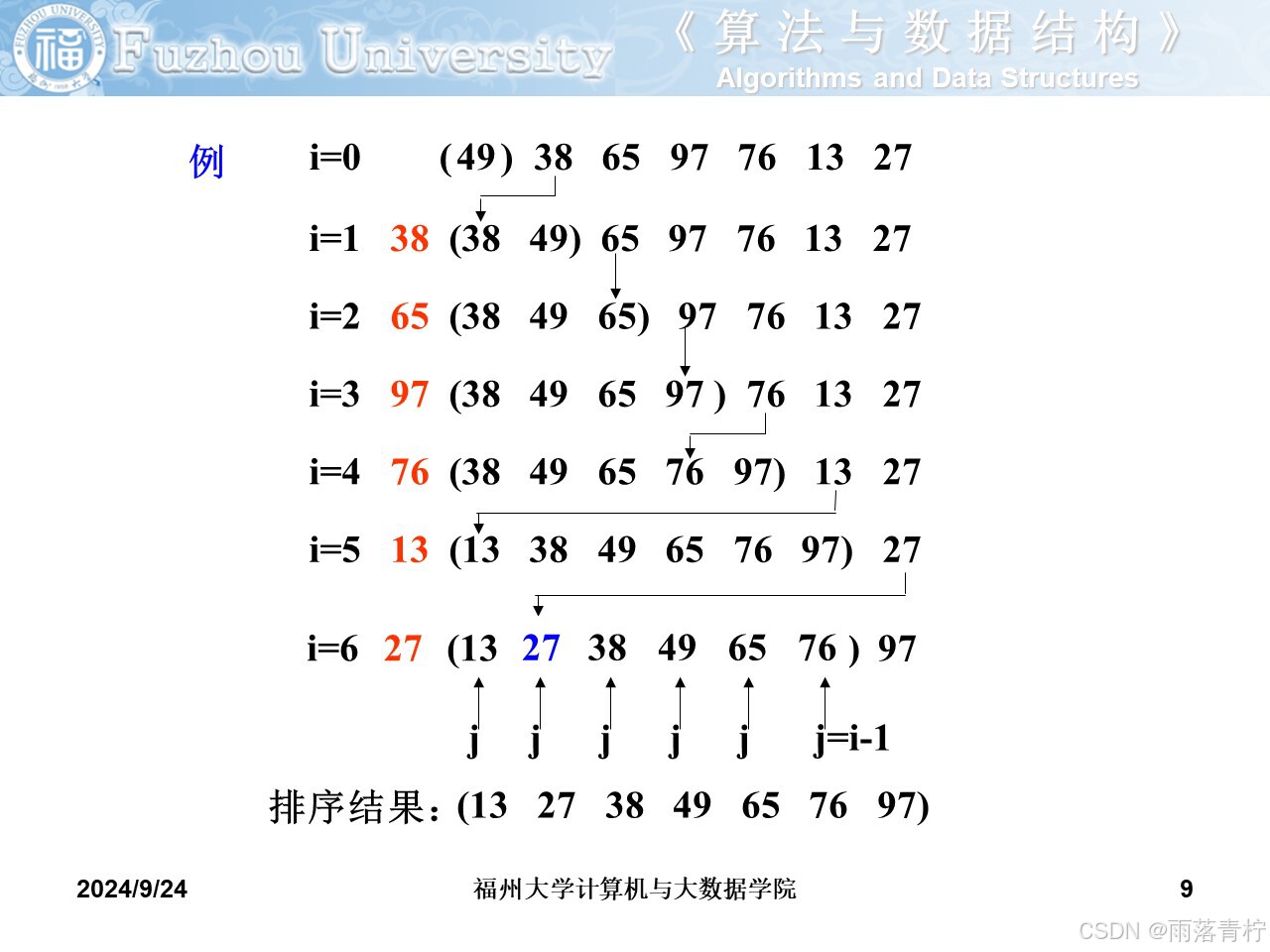
? ? ? ? 插入排序算法
?整個過程為n-1趟排序,即先將序列中第一個記錄看成是一個有序子序列,然后從第二個記錄開始,逐個進行插入,直至整個序列有序。
整個元素插入過程由算法insert來完成
void insert(Item a[],int l,int i)
{Item v=a[i];while(i>1 && less(v,a[i-1])){a[i]=a[i-1];i--;}a[i]=v;
}//插入排序算法通過反復調用insert來完成排序任務void sort(Item a[],int l,int r)
{for(int i=l+1;i<=r;i++)insert(a,l,i);
}? ? ? ? ?二分插入排序
用二分查找方法確定插入位置的排序
? ? ? ? ?希爾排序(縮小增量法)
基本思想:先取一個正整數d1<n,把所有相隔d1的記錄放一組,組內進行直接插入排序;然后取d2<d1,重復上述分組和排序操作;直到di=1,即所有記錄放進一個組中排序為止。


快速排序算法
排序——快速排序(Quick sort)-CSDN博客
typedef int T;
//快速排序算法QuickSort的實現
void QuickSort(T a[], int p, int r) //p,r都是下標
{if (p < r){int q = Partition(a, p, r); //劃分QuickSort(a, p, q - 1); //對左端快速排序QuickSort(a, q + 1, r); //對右端快速排序}
} //對a[0:n-1]快速排序只要調用QuickSort(a,0,n-1)//劃分(Partition)的實現
int Partition(T a[], int p, int r)
{int i = p;int j = r + 1;T x = a[p];while (true){while (a[++i] < x);while (a[--j] > x);if (i >= j)break;Swap(a[i], a[j]);}a[p] = a[j];a[j] = x;return j;
}? ? ? ? 隨機快速排序算法
?在Partition劃分的基準值不固定為數組的第一個值,而是隨機在a[p:r]中挑選
//隨機劃分的實現
int RandomizedPartition(T a[], int p, int r)
{int i = Random(p, r);Swap(a[i], a[p]);return Partition(a, p, r);
}//隨機快速排序算法
void RandomizedQuicckSort(T a[], int p, int r)
{if (p < r){int q = RandomizedPartition(a, p, r);RandomizedPartition(a, p, q - 1);RandomizedPartition(a, q + 1, r);}
}?合并排序算法(非就地)
數據結構和算法:歸并排序(合并排序)詳解_合并排序是采用分治策略實現對n個元素進行排序的算法,是分治法的一個典型應用和完-CSDN博客

?

//非遞歸版的合并排序算法
void MergeSort(T a[], int n)
{T* b = new T[n];int s = 1;while (s < n){MergePass(a, b, s, n); //合并到數組bs += s;MergePass(b, a, s, n); //合并到數組as += s;}
}//需要的函數
//合并x[]中大小為s的相鄰子數組到y[]中
void MergePass(T x[], T[y], int s, int n)
{int i = 0;while (i <= n - 2 * s){Merge(x, y, i, i + s - 1, i + 2 * s - 1);i = i + 2 * s;}//剩下的元素個數少于2sif (i + s < n){Merge(x, y, i, i + s, n - 1);}else{for (int j = i; j <= n - 1; j++){y[i] = x[i];}}
}//有序的合并c[l:m]和c[m+1:r]到d[l:r]
void Merge(T c[], T d[], int l, int m, int r)
{int i = l;j = m + 1;k = l;while ((i <= m) && (j <= r)){if (c[i] <= c[j]){d[k++] = c[i++];}elsed[k++] = c[j++];}if (i > m){for (int q = j; q <= r; q++){d[k++] = c[q]; //c[m+1,r]到位}}else{for (int q = i; q <= m; q++){d[k++] = c[q]; //c[l:m]到位}}
}

特殊有序集的線性時間排序算法???
? ? ? ? 計數排序算法?

//算法的實現
void CountingSort(int m,int a[],int n,int b[])
{int c[m+1];for(int i=0;i<=m;i++){c[i]=0;}for(int i=0;i<n;i++){c[a[i]]+=1;}//c[i]中存放的是a中鍵值對等于i的元素個數for(int i=1;i<=m;i++){c[i]+=c[i-1];}//c[i]中存放的是a中鍵值對小于或等于i的元素個數for(int i=n;i>0;i--){b[c[a[i-1]]-1]=a[i-1];c[a[i-1]]-=1; //具有排序的穩定性}
}
? ? ? ? 桶排序?

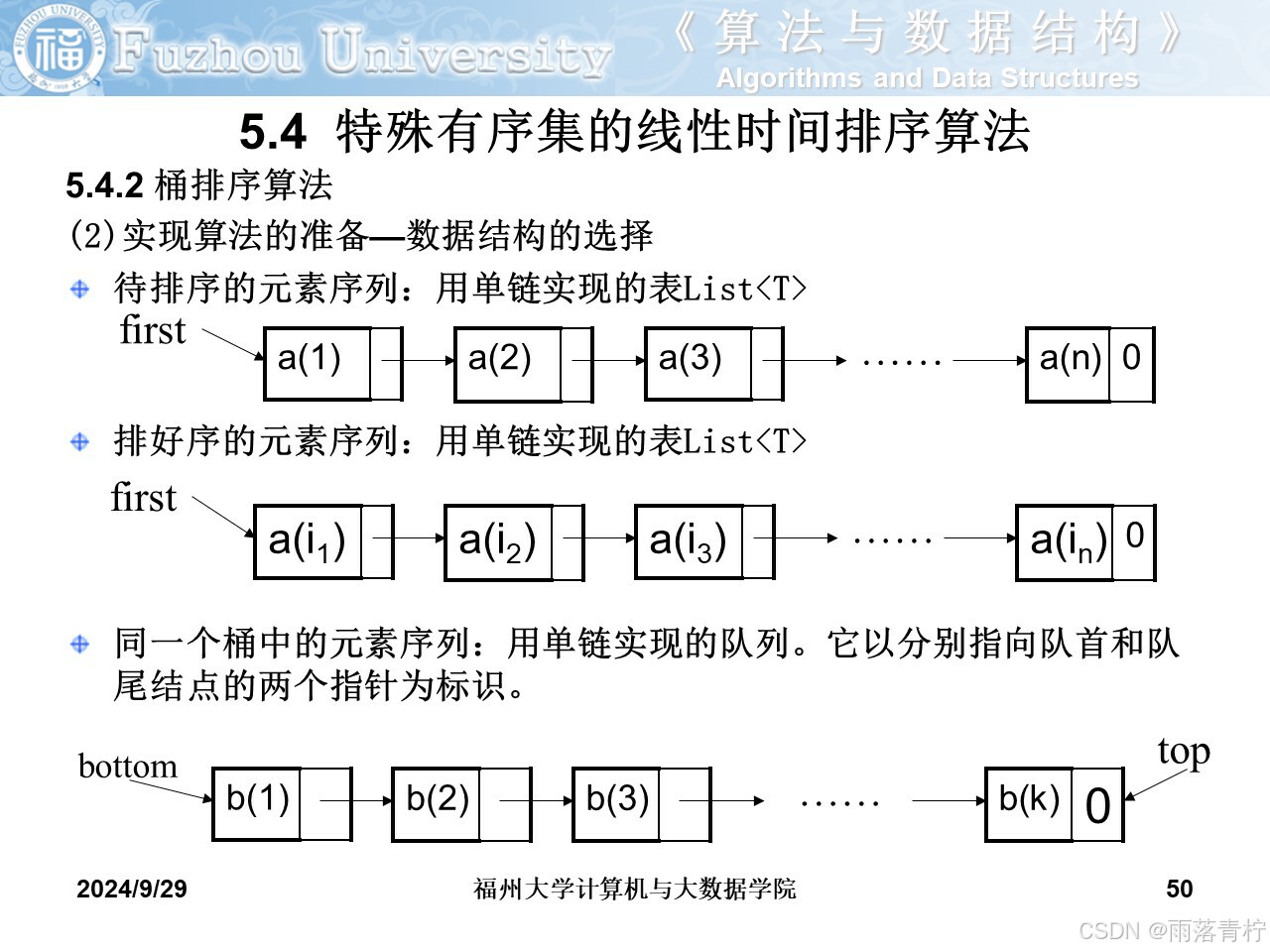

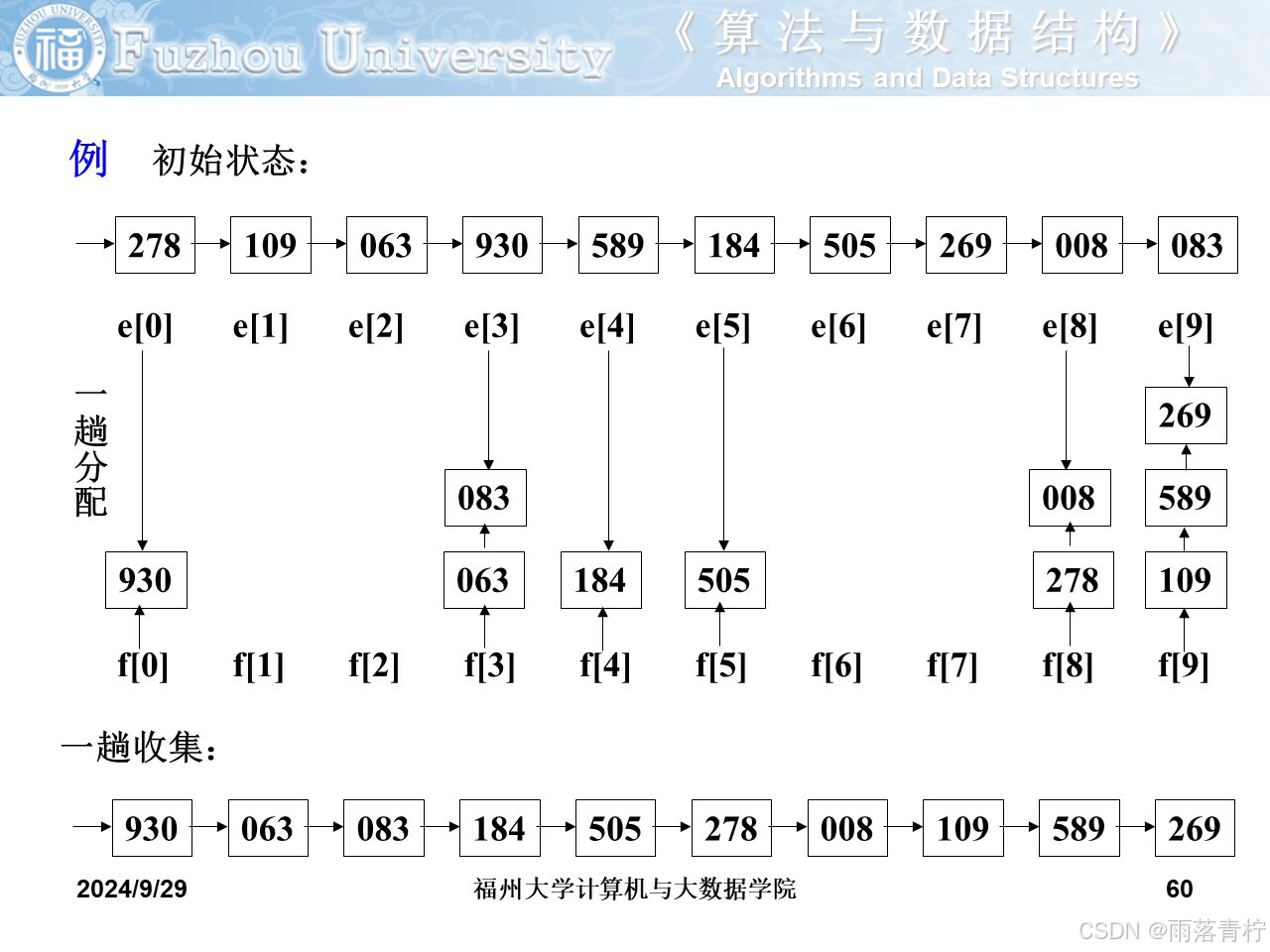
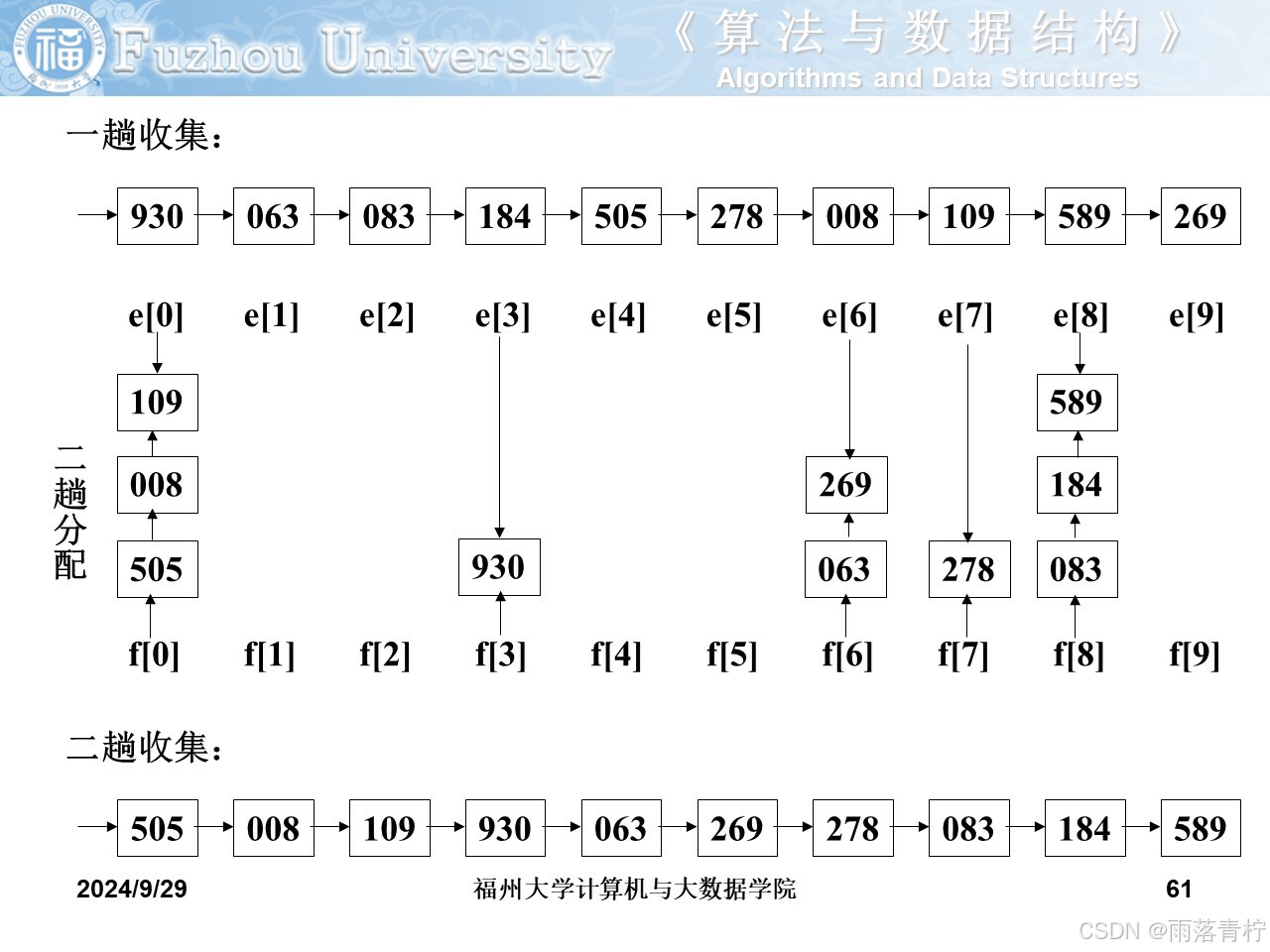
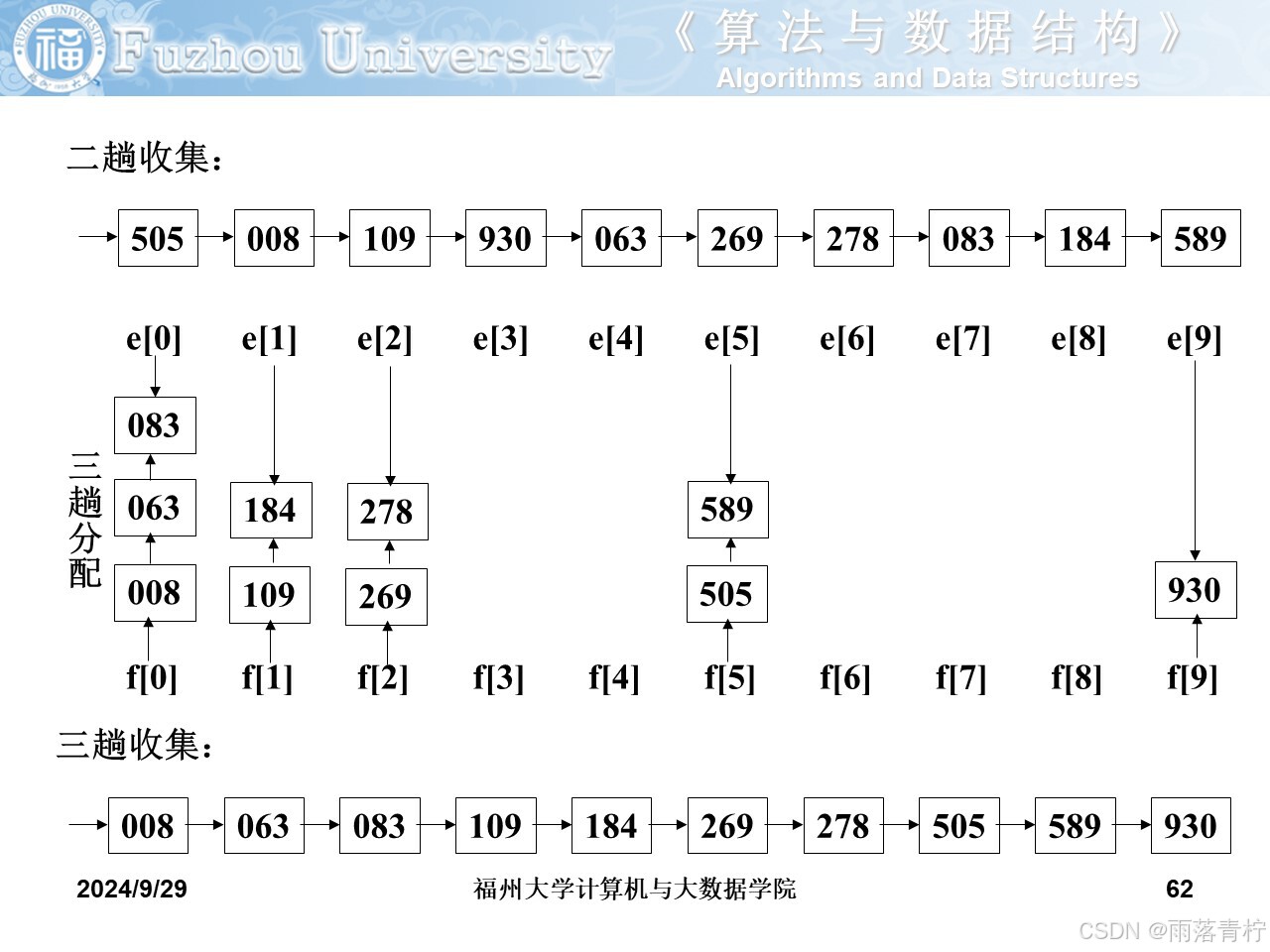
基數排序?
? ? ? ? 多關鍵字排序


 ?
?



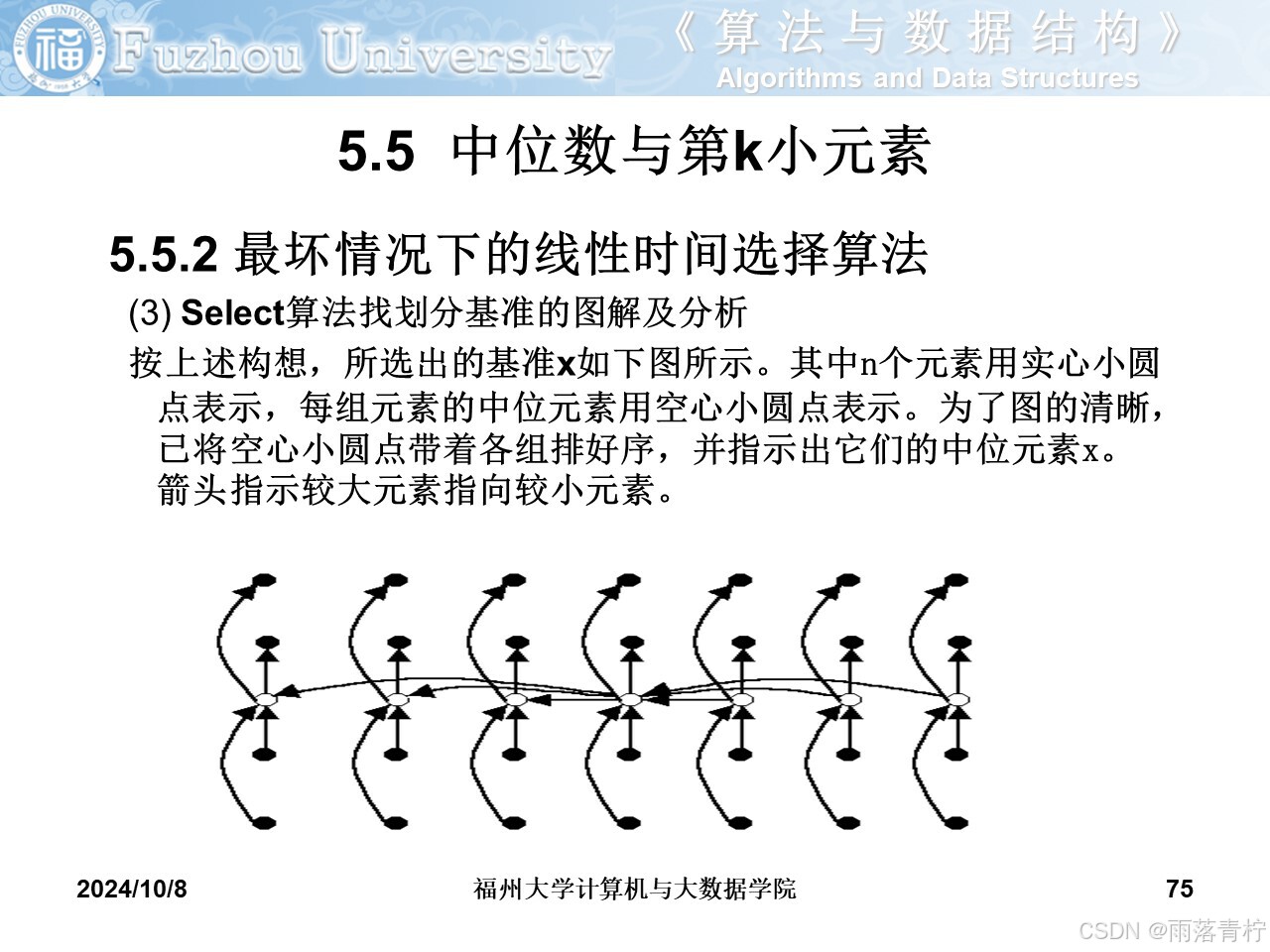
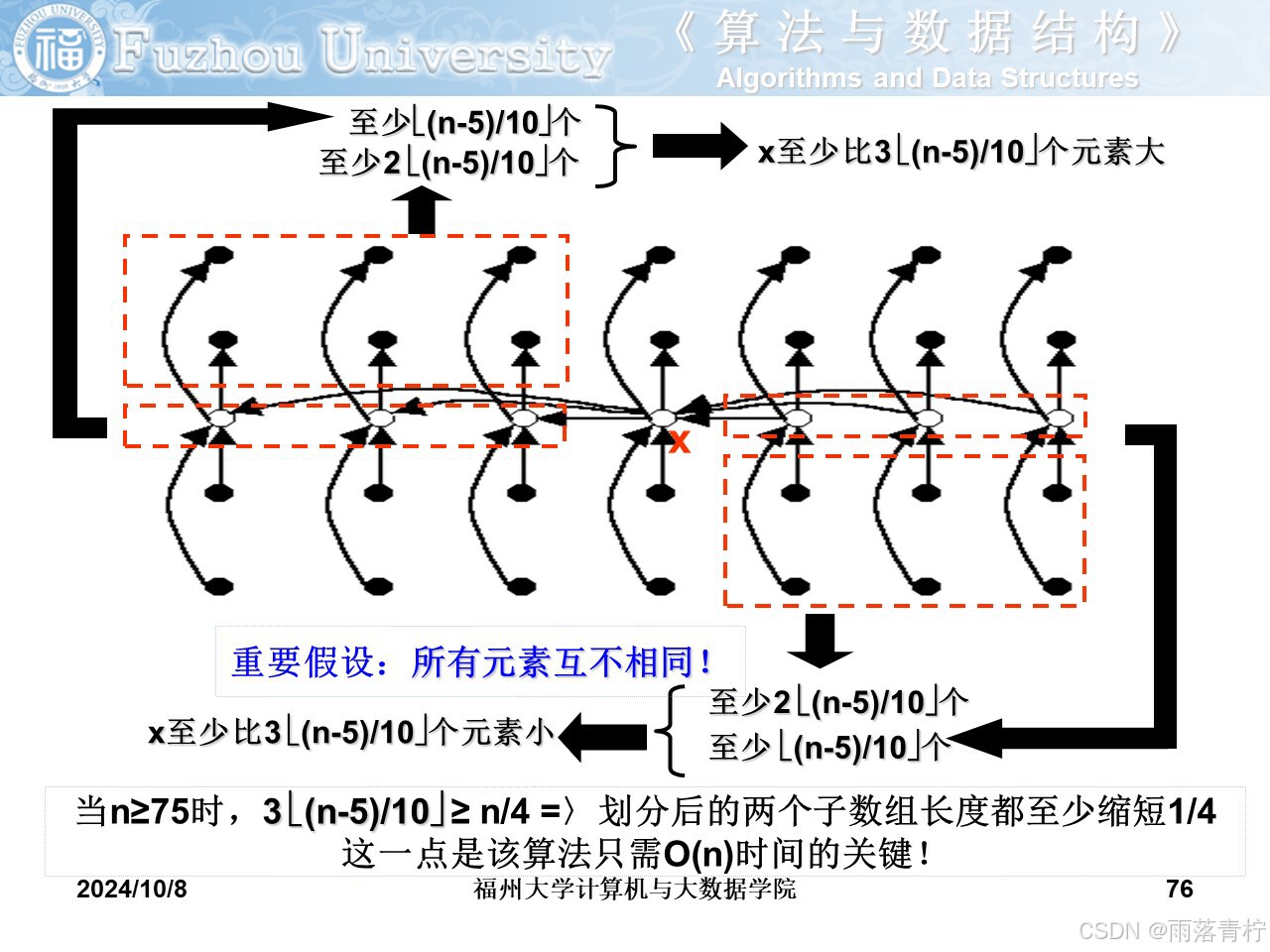
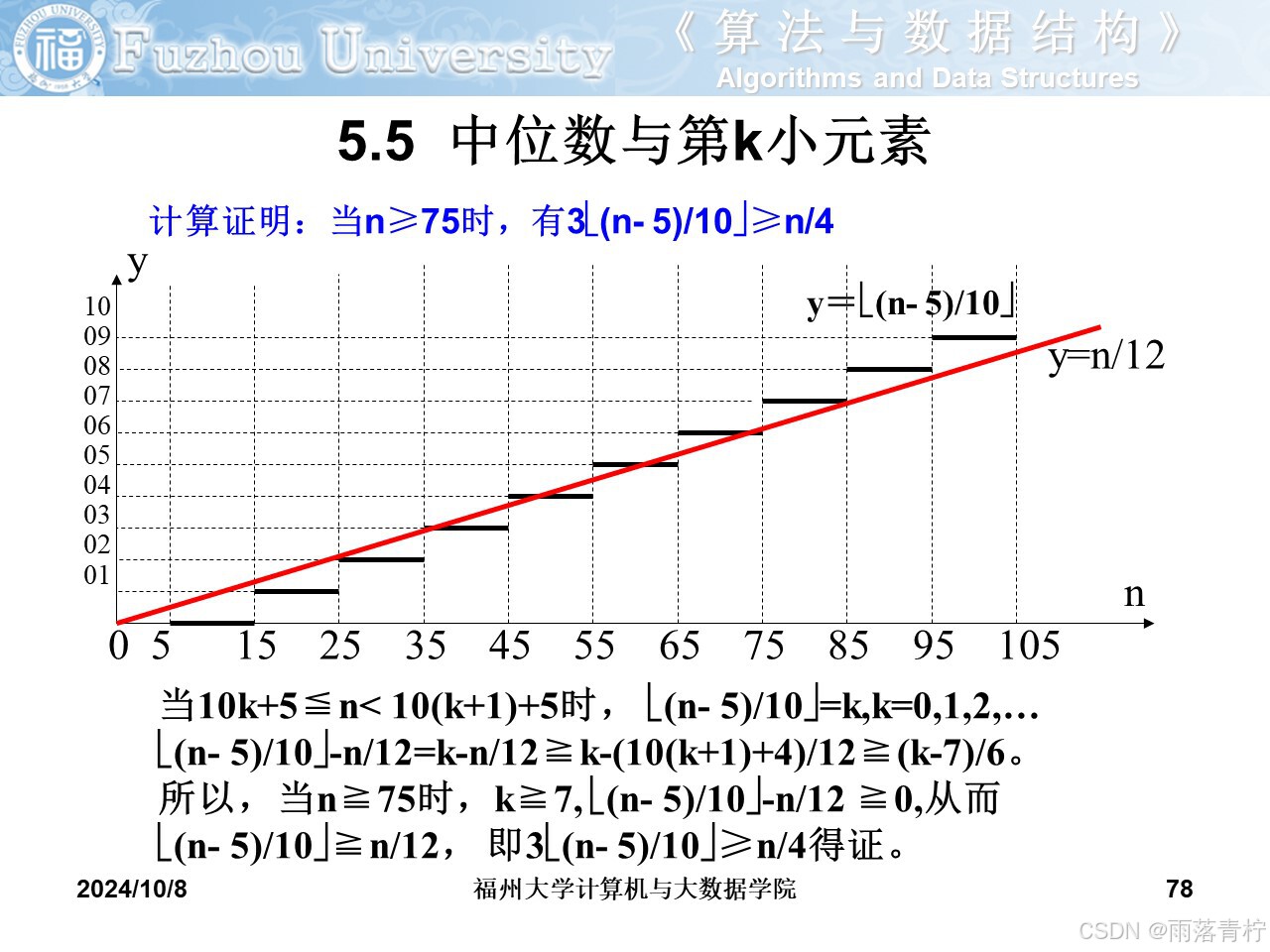
?中位數與第k小元素


T RandomizeSelect(T a[],int p,int r,int k)
//p,r是下標,要求p<=r,1<=k<=r<=r-p+1
{if(p==r)return a[p];int i=RandomizePartition(a,p,r);int j=i-p+1; //左段的元素個數if(k<=j)return RandomizeSelect(a,p,i,k);elsereturn RandomizeSelect(a,i+1,r,k-j);
}
//為在a[0:n-1]中找第k小,只要調用RandomizeSelect(a,0,n-1,k)










 ?
?


)

講解))


)











 文件對話框 QFileDialog 篇二:源碼帶注釋)
