一、基礎算術運算
1. 逐元素運算
a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])# 加減乘除
a + b # [5, 7, 9]
a - b # [-3, -3, -3]
a * b # [4, 10, 18]
a / b # [0.25, 0.4, 0.5]# 冪運算、平方根
a ** 2 # [1, 4, 9]
torch.sqrt(a) # [1.0, 1.414, 1.732]2. 標量運算
a = torch.tensor([1, 2, 3])a + 2 # [3, 4, 5]
a * 3 # [3, 6, 9]二、矩陣運算
?1. 矩陣乘法
a = torch.rand(2, 3) # [2, 3]
b = torch.rand(3, 4) # [3, 4]# 矩陣乘法
a @ b # [2, 4],等價于 torch.matmul(a, b)?2. 批量矩陣乘法
a = torch.rand(10, 2, 3) # [10, 2, 3]
b = torch.rand(10, 3, 4) # [10, 3, 4]# 批量矩陣乘法(每個批次獨立計算)
torch.bmm(a,b) # [10, 2, 4]?總結
輸入形狀 | 輸出形狀 | ||
|---|---|---|---|
|
|
| 每個批次獨立進行矩陣乘法 |
|
|
| 廣播批次維度后進行矩陣乘法 |
|
|
| 標準矩陣乘法 |
|
|
| 廣播后進行矩陣乘法 |
?3. 點積(內積)
a = torch.tensor([1, 2, 3])
b = torch.tensor([4, 5, 6])torch.dot(a, b) # 32(1*4 + 2*5 + 3*6)?三、降維運算
1. 求和、均值、最大值、最小值
a = torch.rand(3, 4)torch.sum(a) # 標量,所有元素和
torch.sum(a, dim=0) # [4],按行求和
torch.mean(a, dim=1) # [3],按列求均值
torch.max(a, dim=0) # 返回 (values, indices) 元組
torch.min(a, dim=1) # 返回 (values, indices) 元組?2. 范數計算
a = torch.tensor([3.0, 4.0])torch.norm(a, p=2) # 5.0(L2范數)
torch.norm(a, p=1) # 7.0(L1范數)? ? 在數學和機器學習中,范數(Norm)?是衡量向量 “大小” 或 “長度” 的一種函數,它為向量空間中的每個向量賦予一個非負實數,表示其 “規模”。范數是歐幾里得距離的推廣,在深度學習中常用于損失函數設計、正則化、優化算法等場景。
(1)、所有范數都滿足以下 3 個基本性質:
非負性:對于任意向量?x,范數?∥x∥≥0,且僅當?x?是零向量時,范數為 0。
齊次性:對于任意標量?α?和向量?x,有?∥αx∥=∣α∣?∥x∥。
三角不等式:對于任意兩個向量?x?和?y,有?∥x+y∥≤∥x∥+∥y∥。
(2)、常見的向量范數(對應?torch.norm?中的?p?參數)?
在 PyTorch 中,torch.norm(a, p)?計算向量?a?的?p - 范數,其中?p?是范數的階數。最常用的有以下幾種:
①?L1 范數(p=1)
定義:向量所有元素的絕對值之和。
公式: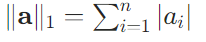
例子:
對于向量?a=[3.0,4.0],∥a∥1?=∣3.0∣+∣4.0∣=3+4=7.0。特點:對異常值(離群點)更敏感,會將大的誤差放大,但計算簡單。
②L2 范數(p=2)
定義:向量所有元素的平方和的平方根(即歐幾里得距離)。
公式: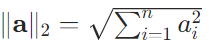
例子:
對于向量?a=[3.0,4.0],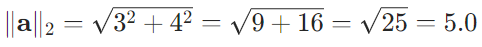
特點:是最常用的范數,對誤差的懲罰更平滑,在機器學習中常用于正則化(防止過擬合)。
?四、三角函數與指數對數
x = torch.tensor([0.0, torch.pi/2, torch.pi])torch.sin(x) # [0.0, 1.0, 0.0]
torch.cos(x) # [1.0, 0.0, -1.0]
torch.tan(x) # [0.0, inf, 0.0]y = torch.tensor([1.0, 2.0, 3.0])torch.exp(y) # [e^1, e^2, e^3]
torch.log(y) # [ln(1), ln(2), ln(3)]五、高級運算
?1. 矩陣分解
a = torch.rand(3, 3)# LU分解
P, L, U = torch.lu(a)# SVD分解
U, S, V = torch.svd(a)?2. 特征值與特征向量
a = torch.rand(3, 3)eigenvalues, eigenvectors = torch.eig(a, eigenvectors=True)?六、統計運算
1. 協方差矩陣
x = torch.rand(10, 3) # 10個樣本,3個特征# 計算協方差矩陣
cov_matrix = torch.cov(x.t()) # [3, 3]?2. 直方圖
x = torch.rand(100)# 計算直方圖
hist = torch.histc(x, bins=10, min=0, max=1)
# input:輸入張量(必須是一維張量)。
# bins:直方圖的分箱數(即柱子數量),默認為 10。
# min:直方圖的最小值范圍,小于此值的元素會被忽略。
# max:直方圖的最大值范圍,大于此值的元素會被忽略。若 max=0,則使用 input 的最大值。











 的解決)





)
