---

摘要

---

翻譯：

確定性神經網絡（NNs）正日益部署在安全關鍵領域，其中校準良好、魯棒且高效的不確定性度量至關重要。本文提出一種新穎方法，用于訓練非貝葉斯神經網絡以同時估計連續目標值及其關聯證據，從而學習偶然和認知不確定性。我們通過在原高斯似然函數上放置證據先驗，并訓練神經網絡推斷證據分布的參數來實現這一目標。此外，我們在訓練中施加先驗約束，當預測證據與正確輸出未對齊時對模型進行正則化。該方法不依賴推理期間的采樣，也無需使用分布外（OOD）樣本進行訓練，從而實現高效且可擴展的不確定性學習。我們在多個基準測試中展示了良好校準的不確定性度量，可擴展至復雜計算機視覺任務，并對抗性樣本和OOD測試樣本具有魯棒性。

研究背景?	安全關鍵領域需要確定性神經網絡的可靠不確定性度量
??創新方法?	1. 使用證據先驗替代傳統高斯似然、2. 網絡直接輸出證據分布超參數
??技術突破?	同時建模： 偶然不確定性（數據噪聲） 認知不確定性（模型置信度）
??訓練機制?	引入證據對齊的正則化項，懲罰預測證據與真實輸出的偏差
??效率優勢?	無需： 推理時采樣、 OOD訓練數據
驗證效果?在以下場景有效	標準基準測試、 復雜CV任務、 對抗/OOD樣本

傳統模式

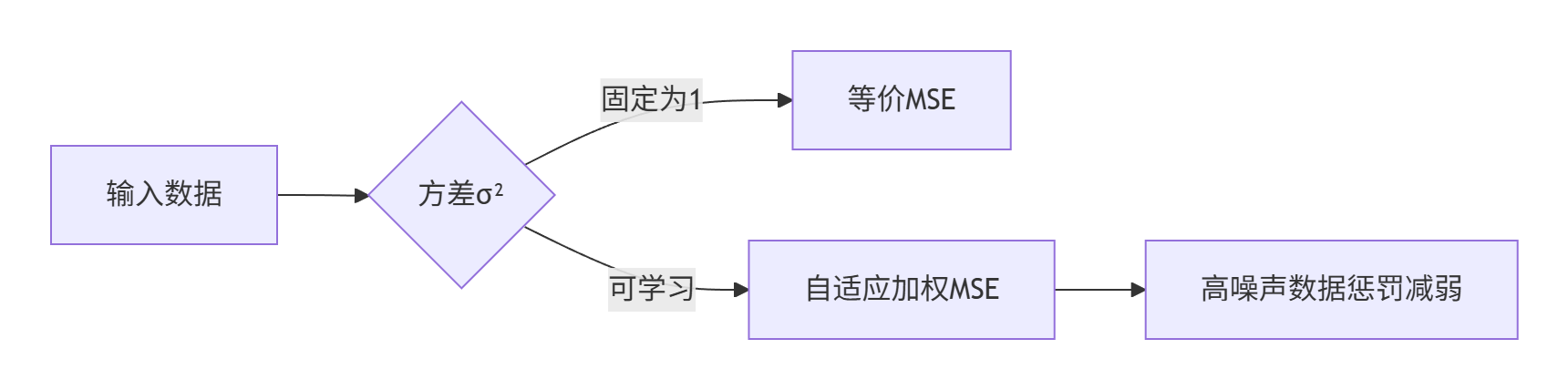
class GaussianNN(nn.Module):def __init__(self, input_dim):super().__init__()self.fc = nn.Linear(input_dim, 2)  # 輸出mu和log_sigmadef forward(self, x):output = self.fc(x)mu = output[:, 0]          # 均值預測log_sigma = output[:, 1]   # 對數方差（數值穩定）sigma = torch.exp(log_sigma)return mu, sigmadef train_step(x, y_true):mu, sigma = model(x)loss = 0.5 * (torch.log(sigma**2) + (y_true - mu)**2 / sigma**2)loss.mean().backward()

案例

1.引言

翻譯

基于回歸的神經網絡（NNs）正被應用于計算機視覺[15]、機器人與控制[1,6]等安全關鍵領域，在這些領域中，推斷模型不確定性的能力對于最終的大規模應用至關重要。此外，精確且校準良好的不確定性估計有助于解釋置信度、捕捉分布外（OOD）測試樣本的領域偏移，并識別模型可能失敗的情況。

神經網絡的不確定性可以分為兩個方面進行建模：(1) 數據中的不確定性，稱為偶然不確定性（aleatoric uncertainty）；(2) 預測中的不確定性，稱為認知不確定性（epistemic uncertainty）。雖然偶然不確定性可以通過數據直接學習，但認知不確定性的估計方法也有多種，例如貝葉斯神經網絡（Bayesian NNs），它在網絡權重上設置概率先驗，并通過采樣來近似輸出方差[25]。然而，貝葉斯神經網絡面臨一些限制，包括在給定數據的情況下難以直接推斷權重的后驗分布、推理過程中需要采樣帶來的計算開銷，以及如何選擇權重先驗的問題。

相比之下，證據深度學習（Evidential Deep Learning）將學習過程形式化為一個證據獲取過程[42,32]。每個訓練樣本都為一個學習到的高階證據分布提供支持。從該分布中采樣可得到低階似然函數的實例，而數據正是從中生成的。不同于貝葉斯神經網絡在網絡權重上設置先驗，證據方法直接對似然函數設置先驗。通過訓練神經網絡輸出高階證據分布的超參數，可以在無需采樣的情況下，學習到有依據的認知和偶然不確定性的表示。

迄今為止，證據深度學習主要面向離散分類問題[42,32,22]，并且通常需要定義明確的距離度量以連接最大不確定性的先驗[42]，或依賴于使用OOD數據進行訓練以提升模型不確定性[32,31]。相比之下，連續回歸問題缺乏明確定義的距離度量來正則化所推斷的證據分布。此外，在大多數應用場景中預先定義合理的OOD數據集并不容易；因此，亟需僅從分布內訓練集中獲得對OOD數據具有校準良好不確定性的方法。

我們提出了一種新的方法，通過學習證據分布來建模回歸網絡的不確定性（如圖1所示）。具體而言，本文做出了以下貢獻：

1. 提出了一種新穎且可擴展的方法，用于在回歸問題中學習認知和偶然不確定性，無需在推理或訓練過程中進行采樣；
2. 提出了適用于連續回歸問題的證據正則化方法，用于懲罰誤差和OOD示例上的錯誤證據；
3. 在基準和復雜的視覺回歸任務上評估了認知不確定性，并與當前最先進的神經網絡不確定性估計技術進行了比較；
4. 在OOD和對抗性擾動的測試輸入數據上評估了魯棒性和校準性能。
   傳統神經網絡vs貝葉斯神經網絡

貝葉斯神經網絡就像個"會承認自己會犯錯"的學霸??

傳統神經網絡（普通學霸）??	貝葉斯神經網絡（謙虛學霸）
??特點??：每次考試都斬釘截鐵給答案	??特點??：會給答案范圍
“這道題答案絕對是3.14！”	“答案可能是3.1到3.2之間，我有80%把握”
實際可能是3.12，但從不告訴你它有多確定	同時告訴你答案和可信度

工作原理類比??
??步驟1：考前劃重點（先驗）??
老師說：“考試重點在1-3章”（這就是先驗知識）
普通學霸：只背這3章，其他完全不看
貝葉斯學霸：重點看1-3章，但也會瞄一眼其他章節
??步驟2：考試答題（訓練）??
發現第4章也考了
貝葉斯學霸：
“看來不能全信老師，要調整復習策略”
→ 更新知識分布（計算后驗)
步驟3：回答不確定的題（預測）??
遇到超綱題時：
普通學霸：硬著頭皮蒙一個答案
貝葉斯學霸：
“這題我沒把握，答案可能在A到D之間”
→ 通過多次思考（采樣）給出概率范圍
4. 為什么需要多次"思考"？??
貝葉斯學霸會這樣做：
第一次想：可能是B
第二次想：也可能是C
…
綜合100次思考結果：
60%概率是B
30%概率是C
10%概率是其他
??最終答案??：最可能是B，但有不確定性（方差）
??貝葉斯實際應用例子??
??醫療診斷場景??：
普通AI：
“患者有80%概率患癌”（醫生可能過度治療）
貝葉斯AI：
“患癌概率60%-85%，因為模型沒見過類似病例”
→ 提醒醫生需要進一步檢查
??貝葉斯關鍵優勢??
??知道什么時候不確定??：遇到沒見過的題型會明說
??能利用經驗??：把老師劃重點的知識融入判斷
??避免過度自信??：不會對蒙的答案打包票
本文

2. 從數據中建模不確定性

3. 回歸中的證據不確定性

NIG分布是高斯分布與逆伽瑪分布的聯合分布

在這里插入代碼片

4.實驗

下面展示了這幾種關系圖

示例像素級深度預測及其不確定性
圖像集展示了不同模型（如Dropout、Ensemble和Evidential）在處理同一場景時的表現。每種模型對應的展示包括：原始RGB圖像、該場景的真實深度圖、模型預測出的深度圖、模型預測誤差的絕對值圖以及模型估計的不確定性圖。
預測置信度水平與觀測誤差的關系
對比了不同方法（同樣包括Dropout、Ensemble和Evidential）在不同的預測置信度水平下的均方根誤差（RMSE）。通過這些曲線，可以直觀地看出隨著置信度的提高，各個模型的誤差變化趨勢，進而評估它們在不同置信度水平上的性能。
模型不確定性的校準情況
校準圖表描繪了模型期望置信度水平與實際觀測到的置信度水平之間的關系。理想情況下，這兩者應該完全吻合（即圖表中的 𝑦 = 𝑥 y=x 線）。此外，還提供了放大版的插圖來詳細展示每個模型的校準誤差，幫助理解不同模型在校準不確定性方面的能力差異。

下面展示了這幾種關系圖

A. Cumulative density function (CDF) of ID and OOD entropy for tested methods
這部分通過累積密度函數(CDF)展示了不同方法(ID vs OOD)在熵上的分布情況。它可以幫助我們理解不同模型在識別OOD樣本時的能力，理想情況下OOD樣本應具有更高的熵值。
B. Uncertainty (entropy) comparisons across methods
此部分使用箱形圖對比了不同方法在ID與OOD數據集上的熵值。這有助于直觀地比較各種方法在不確定性估計上的差異，尤其是在區分ID和OOD數據方面。
C. Full density histograms of entropy estimated by evidential regression on ID and OOD data
展示了基于證據回歸方法對ID和OOD數據估算出的熵值的概率密度直方圖。這有助于深入了解不同數據集下模型輸出的不確定性分布情況。
D. Sample images
提供了一些樣本圖像的例子，包括RGB輸入、預測深度圖以及對應的熵圖。這部分通常用于視覺化展示模型預測結果及其不確定性區域，幫助理解和解釋模型的行為。

下面展示了這幾種關系圖

RMSE vs Noise ε：展示了對抗噪聲強度與均方根誤差（RMSE）之間的關系。
Uncertainty vs Noise ε：展示了對抗噪聲強度與估計的不確定性之間的關系。
CDF of Entropy：顯示了不同對抗噪聲強度下熵的累積分布函數（CDF）。
Visualization of Increasing Adversarial Perturbation：通過一系列圖像展示了隨著對抗擾動增加，輸入圖像、深度標簽、預測深度、絕對誤差及預測不確定性的變化情況。

補充知識：t分布