歡迎關注[【AIGC論文精讀】](https://blog.csdn.net/youcans/category_12321605.html）原創作品
【DeepSeek論文精讀】1. 從 DeepSeek LLM 到 DeepSeek R1
【DeepSeek論文精讀】10. DeepSeek-Coder-V2: 突破閉源模型在代碼智能領域的障礙
【DeepSeek論文精讀】12. DeepSeek-Prover-V2: 通過強化學習實現子目標分解的形式化數學推理

0. DeepSeek-Prover-V2 模型介紹

DeepSeek-Prover-V2 是由 DeepSeek 團隊開發的開源大型語言模型，專注于形式化數學定理證明，尤其在 Lean 4 平臺上的表現達到行業領先水平。該模型通過結合非形式化推理與形式化驗證，實現了數學直覺與符號邏輯的雙向對齊，標志著AI在數學推理領域的重大突破。

0.1 模型概述

參數規模與架構

• 雙版本發布：包含 DeepSeek-Prover-V2-671B（6710億參數）和 DeepSeek-Prover-V2-7B（70億參數）兩個版本。前者基于DeepSeek-V3架構，采用混合專家系統（MoE），每層包含256個路由專家和1個共享專家，支持超長上下文（最長163,840 tokens）和多精度計算（如FP8量化）1510。

• 專精數學推理：不同于通用對話模型，其設計目標聚焦于形式化定理證明，生成兼容Lean 4的嚴謹證明步驟，適用于自動驗證、教學輔助及數學發現等場景14。

核心創新

• 遞歸定理證明流程：通過DeepSeek-V3模型將復雜問題分解為子目標（subgoals），生成自然語言證明草圖和Lean 4形式化框架，再通過7B模型遞歸解決子目標并合成完整證明。

• 冷啟動數據生成：結合非形式化的思維鏈（CoT）與形式化證明步驟，生成高質量的初始訓練數據，為強化學習提供基礎。

0.2 關鍵技術

訓練流程

• 冷啟動階段：利用DeepSeek-V3分解問題并生成子目標，通過7B模型解決子目標后，將證明與CoT結合，形成初始訓練數據。

• 強化學習優化：采用 GRPO算法（群體相對策略優化），以二元獎勵（正確為1，錯誤為0）驅動模型優化，增強形式化證明與初始推理的一致性。

• 兩階段訓練：

  • 非CoT模式：快速生成簡潔的Lean代碼，提升響應效率。

  • CoT模式：通過結構化思維鏈和強化學習，提升邏輯嚴謹性。

課程學習與數據增強

• 通過子目標生成不同難度的定理，逐步增加訓練任務復雜度，引導模型學習復雜證明。

• 篩選7B模型無法端到端解決但子目標已證明的問題，構建合成數據以增強泛化能力。

0.3 性能表現

• 基準測試成績

  • MiniF2F-test：通過率高達88.9%（Pass@8192），創下神經定理證明領域的新紀錄。

  • PutnamBench：解決658個問題中的49個，展現大學水平數學問題的處理能力。

  • AIME競賽題：在15道高中競賽級題目中解決6道，而通用模型DeepSeek-V3通過多數表決解決8道，顯示形式化與非形式化推理差距顯著縮小。

• 擴展評估

  • ProverBench數據集：包含325個形式化問題，涵蓋高中競賽（如AIME 24-25）和本科數學（如線性代數、微積分），為多樣化場景評估提供標準。

  • 跨領域泛化：在組合數學基準CombiBench中解決12/77問題，展示跨學科潛力。

DeepSeek-Prover-V2通過創新的子目標分解與強化學習策略，成功彌合了非形式化推理與形式化驗證的鴻溝，成為數學AI領域的標桿。其高性能與開源特性為學術界和工業界提供了強大工具，未來或可擴展至國際數學奧林匹克（IMO）級別問題的挑戰。

0.4 論文簡介

• 論文標題：DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition（DeepSeek-Prover-V2: 通過強化學習實現子目標分解的形式化數學推理）
• 發布時間：2025 年 4 月
• 論文作者：Z.Ren, ZhihongShao, JunxiaoSong, HuajianXin, et al.
• 下載地址：arxiv: Deepseek-Prover-V2
  Hugging Face：https://huggingface.co/deepseek-ai/DeepSeek-Prover-V2-671B
  GitHub：https://github.com/deepseek-ai/DeepSeek-Prover-V2/tree/main


0.5 摘要

我們介紹DeepSeek-Prover-V2，這是一個專為Lean 4形式化定理證明設計的開源大型語言模型，其初始化數據通過由DeepSeek-V3驅動的遞歸定理證明流程收集。冷啟動訓練流程首先提示DeepSeek-V3將復雜問題分解為一系列子目標。已解決子目標的證明被合成為思維鏈過程，與DeepSeek-V3的逐步推理相結合，為強化學習創建初始冷啟動。該流程使我們能夠將非形式化和形式化數學推理整合到統一模型中。

最終模型DeepSeek-Prover-V2-671B在神經定理證明中實現最先進性能，達到MiniF2F-test 88.9%的通過率，并解決了PutnamBench 658個問題中的49個。除標準基準測試外，我們引入ProverBench（包含325個形式化問題的集合）以豐富評估體系，包括從近期AIME競賽（第24-25屆）精選的15個問題。針對這15個AIME問題的進一步評估顯示，模型成功解決了其中6個。相比之下，DeepSeek-V3通過多數表決方法解決了其中8個問題，這表明大型語言模型中形式化與非形式化數學推理之間的差距正在顯著縮小。

1. 引言

大型語言模型 （LLM） 中推理能力的出現徹底改變了人工智能的許多領域，尤其是在數學問題解決領域 （DeepSeek-AI，2025 年）。 這些進步在很大程度上是由推理時間縮放的范式實現的，最明顯的是通過自然語言思維鏈推理 （Jaech et al., 2024）。LLM 不是僅僅依靠一次向前傳遞來得出答案，而是可以反思中間推理步驟，從而提高準確性和可解釋性。盡管自然語言推理在解決競賽級別的數學問題方面取得了成功，但它在形式定理證明中的應用仍然具有根本的挑戰性。LLM 以本質上非形式化化的方式執行自然語言推理，依賴于啟發式、近似和數據驅動的猜測模式，這些模式通常缺乏形式化化驗證系統所需的嚴格結構。相比之下，Lean （Moura and Ullrich， 2021）、Isabelle （Paulson， 1994） 和 Coq （Barras et al., 1999） 等證明助手在嚴格的邏輯基礎上運行，其中每個證明步驟都必須明確構建和形式驗證。這些系統不允許歧義、隱含的假設或遺漏細節。彌合非形式化化、高級推理和形式驗證系統的句法嚴謹性之間的差距仍然是神經定理證明的一個長期研究挑戰 （Yang et al., 2024）。

為了利用非形式化化數學推理的優勢來支持形式定理證明，一種經典方法是在自然語言證明草圖的指導下分層分解形式證明。（Jiang et al. 2023） 提出了一個稱為草稿、草圖和證明 （DSP） 的框架，該框架利用大型語言模型以自然語言生成證明草圖，然后將其轉換為形式化化的證明步驟。這種非形式化化到形式化化的定理證明范式與分層強化學習中的子目標概念密切相關 （Barto 和 Mahadevan，2003 年; Nachum 等 人，2018 年;Eppe et al., 2022）， 其中復雜的任務被分解為更簡單的子任務層次結構，這些子任務可以獨立解決以逐步實現總體目標。在形式化化定理證明中，子目標通常是有助于證明更大定理的中間命題或引理 （Zhao et al., 2023， 2024）。 這種分層分解與人類解決問題的策略保持一致，并支持模塊化、可重用性和更高效的證明搜索 （Wang et al., 2024b;Zheng et al., 2024） 的最近的研究通過采用多層層次結構來生成結構化證明 （Wang et al., 2024a）， 并利用強化學習技術將復雜定理優化為可管理的子目標 （Dong et al., 2024）， 從而擴展了這種范式。

在本文中，我們開發了一個用于子目標分解的推理模型，利用一套合成冷啟動數據和大規模強化學習來提高其性能。 為了構建冷啟動數據集，我們開發了一個簡單而有效的遞歸定理證明管道，利用 DeepSeek-V3 （DeepSeek-AI， 2024） 作為子目標分解和形式化化的統一工具。我們提示 DeepSeek-V3 將定理分解為高級證明草圖，同時在 Lean 4 中將這些證明步驟形式化化，從而產生一系列子目標。由于子目標分解由大型通用模型提供支持，因此我們使用較小的 7B 模型來處理每個子目標的證明搜索，從而減少相關的計算負擔。此外，我們引入了一個課程學習框架，該框架利用分解的子目標生成猜想定理，逐步增加訓練任務的難度，以更好地指導模型的學習過程。一旦解決了具有挑戰性的問題的分解步驟，我們將完整的分步形式證明與 DeepSeek-V3 中的相應思路配對，以創建冷啟動推理數據。在冷啟動的基礎上，應用后續的強化學習階段，以進一步加強非形式化化數學推理和形式證明構造之間的聯系。我們的實驗表明，在任務分解中，從非形式化化推理的冷啟動開始的強化學習顯著提高了模型的形式定理證明能力。由此產生的 DeepSeek-Prover-V2-671B 模型在多個基準測試中建立了最先進的神經定理證明。在 MiniF2F 測試中，它達到 82.4% Pass@32 的準確性，提高到 88.9% Pass@8192。 該模型顯示出對大學水平定理證明的強大泛化能力，使用 Pass@1024 解決
37.1% ProofNet 測試問題，并解決 658 個具有挑戰性的 PutnamBench 問題中的 49 個。此外，我們還貢獻了 ProverBench，這是一個包含 325 個形式化化問題的基準數據集，以推進神經定理證明研究，其中包括來自著名的 AIME 競賽（24-25 歲）的 15 個問題。DeepSeek-Prover-V2-671B 成功解決了這 15 個具有挑戰性的 AIME 問題中的 6 個，進一步展示了其復雜的數學推理能力。

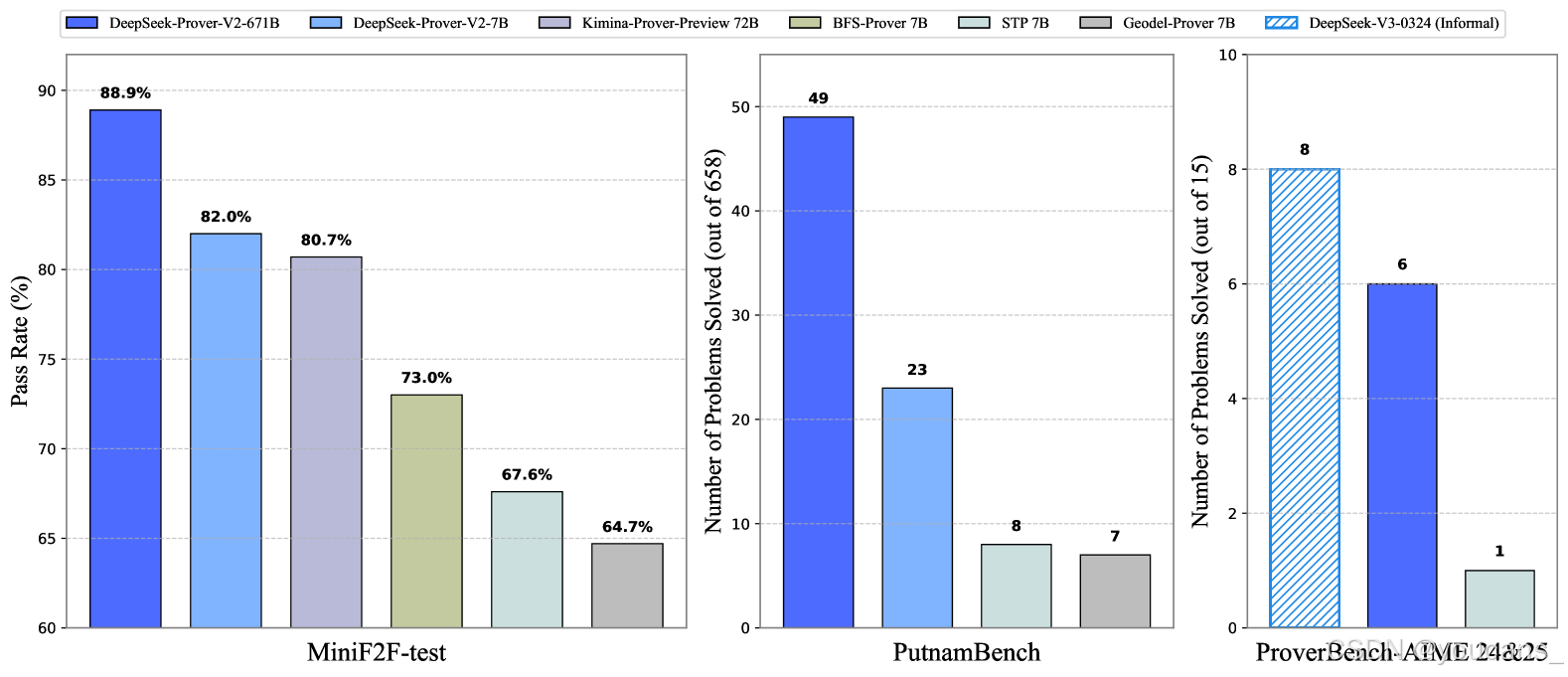
圖 1：DeepSeek-Prover-V2 的基準測試性能。在 AIME 基準測試中，DeepSeek-V3 使用用于自然語言推理的標準查找-答案任務進行評估，而證明者模型生成精益代碼，為給定的正確答案構建形式證明。

圖 2：DeepSeek-Prover-V2 采用的冷啟動數據收集過程概述。
我們首先提示 DeepSeek-V3 生成自然語言的證明草圖，同時將其形式化化為精益聲明，并為遺漏的證明細節添加占位符。然后，一個 7B 證明器模型遞歸地求解分解的子目標。通過組合這些子目標證明，我們為原始復雜問題構建了一個完整的形式化化證明。這個組合證明被附加到 DeepSeek-V3 的原始思維鏈中，為形式化化的數學推理創建高質量的冷啟動訓練數據。

2. 方法

2.1 通過子目標分解進行遞歸證明搜索

將復雜定理的證明分解為一系列較小的引理，作為墊腳石是人類數學家通常采用的有效策略。先前的幾項研究在神經定理證明的背景下探索了這種分層策略，旨在通過利用現代 LLM 的非形式化化推理能力來提高證明搜索效率 （Jiang et al., 2023;Zhao et al., 2023;Wang et al., 2024a;Dong et al., 2024） 的在本文中，我們開發了一個簡單而有效的管道，它利用 DeepSeek-V3 （DeepSeek-AI, 2024） 作為形式定理證明中子目標分解的統一工具。

從自然語言推理中繪制形式證明草圖

大型語言模型的最新進展導致了非形式化化推理能力的重大突破。為了彌合形式化化和非形式化化推理之間的差距，我們利用尖端的通用 LLM，以其強大的數學推理和指令跟蹤能力而聞名，來構建我們定理證明系統的基礎框架。我們的研究結果表明，現成的模型，如 DeepSeek-V3 （DeepSeek-AI， 2024）， 能夠分解證明步驟并用形式語言表達它們。為了證明給定的形式化化定理陳述，我們提示 DeepSeek-V3 首先用自然語言分析數學問題，然后將證明分解為更小的步驟，將每個步驟轉換為相應的精益形式化化陳述。由于眾所周知，通用模型難以生成完整的精益證明，因此我們指示 DeepSeek-V3 僅生成省略細節的高級證明草圖。由此產生的思路鏈最終形成一個精益定理，該定理由一系列陳述組成，每個陳述都以一個令人遺憾的占位符結束，表示要解決的子目標。這種方法反映了人類的證明構造風格，其中復雜定理逐漸簡化為一系列更易于管理的引理。

圖 3： 我們如何將分解的子目標轉換為一系列引理語句的說明性示例。我們首先 （a） 替換原始目標狀態，然后 （b） 將前面的子目標作為前提。語句類型 （b） 用于遞歸解決復雜問題，而類型 （a） 和 （b） 都被納入課程學習過程。

子目標的遞歸解析

利用 DeepSeek-V3 生成的子目標，我們采用遞歸求解策略來系統地解決每個中間證明步驟。我們從語句中提取子目標表達式，以替換給定問題中的原始目標（見圖 3（a）），然后將前面的子目標作為前提（見圖 3（b））。這種構造使得后續的子目標能夠使用早期步驟的中間結果來解決，從而促進更本地化的依賴結構，并促進更簡單詞元的開發。為了減少大量證明搜索的計算開銷，我們采用了一個更小的 7B 證明器模型，專門針對處理分解的引理進行了優化。在成功求解所有分解步驟后，可以自動推導出原始定理的完整證明。

基于子目標的定理證明的課程學習。

證明模型的訓練需要大量的形式化化語言問題集，通常是通過形式化化現有的自然語言數學語料庫得出的（Xin et al., 2024a;Ying et al., 2024;Lin et al., 2025） 的盡管人工創作的文本的形式化化提供了高質量和多樣化的形式化化內容，但證明者模型的結果訓練信號通常很少，因為很大一部分計算嘗試沒有產生成功的證明，因此沒有提供積極的獎勵信號。為了生成更密集的訓練信號，Dong 和 馬 （2025） 提出了一種自游戲方法，通過生成與原始定理陳述密切相關的可處理猜想來豐富訓練問題集，從而更有效地使用訓練計算。在本文中，我們實現了一種簡單的方法，利用子目標來擴展用于模型訓練的形式化化語句的范圍。我們生成了兩種類型的子目標定理，一種將前面的子目標作為前提，另一種沒有，分別對應于圖 3（b） 和圖 3（a）。這兩種類型都被整合到專家迭代階段 （Polu 和 Sutskever，2020 年）， 建立了一個課程，逐步指導證明者模型系統地解決精心策劃的挑戰性問題子集。該程序建立在與 AlphaProof 的測試時強化學習 （DeepMind，2024 年） 相同的基本原理之上，其中生成目標問題的變化以增強模型解決具有挑戰性的 IMO 級問題的能力。

2.2 元統一非形式化化推理和證明形式化化

上面討論的算法框架分兩個階段運行，利用兩個互補的模型：DeepSeek-V3 用于引理分解，7B 證明模型用于完成相應的形式化化證明細節。該管道通過將語言模型的高級推理與精確的形式驗證相結合，為合成形式推理數據提供了一種自然且可擴展的機制。通過這種方式，我們將非形式化化數學推理和證明形式化化的能力統一在一個模型中。

通過合成數據進行冷啟動。

我們以端到端的方式策劃了 7B 證明器模型仍未解決的具有挑戰性的問題子集，但所有分解的子目標都已成功解決。通過組合所有子目標的證明，我們為原始問題構建了一個完整的形式證明。然后將此證明附加到 DeepSeek-V3 的思維鏈中，該思維鏈概述了相應的引理分解，從而產生了非形式化化推理和隨后的形式化化的內聚綜合。它支持收集數百個高質量的合成冷啟動數據，這些數據作為訓練 DeepSeek-Prover-V2 的基礎。這種冷啟動數據集生成策略不同于 Kimina-Prover （Wang et al., 2025） 的策略，后者是形式推理模型的同步工作。具體來說，我們通過將自然語言證明直接形式化化為結構化的形式化化證明草圖來合成數據。相比之下，Kimina-Prover 采用了相反的工作流程：它首先收集完整的形式化化證明以及非形式化化的證明，然后使用通用推理模型將中間自然語言推理步驟逆向合成為連貫的思維塊。

面向推理的強化學習。

在合成冷啟動數據上微調證明者模型后，我們執行強化學習階段，以進一步增強其將非形式化化推理與形式證明構建聯系起來的能力。遵循推理模型的標準訓練目標 （DeepSeek-AI， 2025）， 我們使用二進制正確或錯誤的反饋作為獎勵監督的主要形式。在訓練過程中，我們觀察到生成的證明的結構經常與思維鏈指導提供的引理分解不同。為了解決這個問題，我們在訓練的早期步驟中加入了一致性獎勵，它懲罰了結構錯位，明確強制在最終證明中包含所有分解的結構化引理。在實踐中，強制執行這種對齊可以提高證明的準確性，尤其是在需要多步推理的復雜定理上。

2.3 DeepSeek-Prover-V2 的訓練詳情

兩階段訓練。

DeepSeek-Prover-V2 是通過一個兩階段的訓練管道開發的，該管道建立了兩種互補的證明生成模式：

1. 高效非思維鏈 （non-CoT） 模式：該模式針對形式化化精益證明代碼的快速生成進行了優化，專注于生成簡潔的證明，沒有明確的中間推理步驟。

2. 高精度思維鏈 （CoT） 模式：該模式系統地闡明中間推理步驟，強調透明度和邏輯進展，然后構建最終的形式證明。

與 DeepSeek-Prover-V1.5 （Xin et al., 2024b） 一致，這兩種生成模式由兩個不同的引導提示控制（示例見附錄 A）。在第一階段，我們在課程學習框架內采用專家迭代來訓練非 CoT 證明者模型，同時通過基于子目標的遞歸證明來綜合難題的證明。選擇非 CoT 生成模式是為了加速迭代訓練和數據收集過程，因為它提供了明顯更快的推理和驗證周期。在此基礎上，第二階段利用了通過將 DeepSeek-V3 的復雜數學推理模式與我們的合成形式證明集成而合成的冷啟動思維鏈 （CoT） 數據。CoT 模式通過進一步的強化學習階段得到增強，遵循通常用于推理模型的標準訓練管道。

專家迭代。

DeepSeek-Prover-V2 的非 CoT 模式的訓練程序遵循專家迭代的范式 （Polu 和 Sutskever，2020）， 這是一個廣泛采用的開發形式定理證明器的框架。在每次訓練迭代中，當前最佳證明者策略用于為那些在先前迭代中仍未解決的具有挑戰性的問題生成證明嘗試。這些成功的嘗試由 Lean proof Assistant 驗證，將被合并到 SFT 數據集中，以訓練改進的模型。這種迭代循環確保模型不僅從初始演示數據集中學習，而且還提取出自己的成功推理軌跡，逐步完善其解決更難問題的能力。整體訓練程序與 DeepSeek-Prover-V1 （Xin et al., 2024a） 和 DeepSeek-Prover-V1.5 （Xin et al., 2024b） 基本一致，訓練題的分布只有兩處修改。首先，我們整合了來自自形式化化和各種開源數據集的其他問題 （Ying et al., 2024;董和馬，2025 年;Lin et al., 2025） 的研究中進行了研究，擴大了訓練問題領域的覆蓋范圍。其次，我們用子目標分解產生的問題來增強數據集，旨在解決 MiniF2F 基準的有效拆分中更具挑戰性的實例 （Zheng et al., 2022）。

監督微調。

我們在 DeepSeek-V3-Base-671B （DeepSeek-AI， 2024） 上執行監督微調，在 16,384 個標記的上下文窗口內使用 5e-6 的恒定學習率。我們的訓練語料庫由兩個互補來源組成：（1） 通過專家迭代收集的非 CoT 數據，無需中間推理步驟即可生成精益代碼;（2） 第 2.2 節 中描述的冷啟動 CoT 數據，它將 DeepSeek-V3 的高級數學推理過程提煉成結構化的證明路徑。非 CoT 組件強調精益定理證明器生態系統中的形式驗證技能，而 CoT 示例明確模擬了將數學直覺轉化為形式證明結構的認知過程。

強化學習。

我們采用集團相對策略優化 （GRPO;Shao et al., 2024） 作為我們的強化學習算法，該算法在推理任務中表現出卓越的有效性和效率 （DeepSeek-AI，2025）。 與 PPO （Schulman et al., 2017） 不同，GRPO 通過為每個定理提示對一組候選證明進行采樣并根據它們的相對獎勵優化策略，消除了對單獨批評模型的需求。訓練利用二元獎勵，其中每個生成的 Lean 證明在驗證正確時獲得 1 的獎勵，否則獲得 0 的獎勵。為了確保有效的學習，我們策劃了訓練提示，以僅包含具有足夠挑戰性但可以通過監督微調模型解決的問題。在每次迭代期間，我們對 256 個不同的問題進行采樣，每個定理生成 32 個候選證明，最大序列長度為 32,768 個標記。

蒸餾。

我們將 DeepSeek-Prover-V1.5-Base-7B （Xin et al., 2024b） 的最大上下文長度從 4,096 個標記擴展到 32,768 個標記，并使用在 DeepSeek-Prover-V2-671B 的強化學習階段收集的推出數據微調這個擴展上下文模型。除了 CoT 推理模式外，我們還整合了在專家迭代期間收集的非 CoT 證明數據，以實現一種經濟高效的證明選項，從而使用小規模模型生成簡潔的形式化化輸出。此外，我們執行了與 671B 模型訓練中使用的相同強化學習階段，以提高 DeepSeek-Prover-V2-7B 的性能。

3. 試驗結果

在本節中，我們介紹了 DeepSeek-Prover-V2 在形式定理證明的各種基準數據集中的系統評估，涵蓋高中競賽問題和本科階段的數學。DeepSeek-Prover-V2 的所有實驗結果均使用 Lean 4.9.0 進行，使用與 DeepSeek-Prover-V1.5 相同的測試環境 （Xin et al., 2024b）。 無需進一步說明，基線評估結果來源于各自的原始論文。

3.1 MiniF2F 基準測試的結果

MiniF2F

MiniF2F（Zheng et al., 2022） 由 488 個形式化化的問題陳述組成，這些問題陳述來自各種數學材料，包括 AIME、AMC 和 IMO 競賽，以及來自 MATH 數據集的選定問題 （Hendrycks et al., 2021）。 該基準測試包括涵蓋初等數學核心領域的奧林匹克級別問題，包括代數、數論和歸納。這些問題被分為兩個大小相等的子集，分別用 miniF2F-valid 和 miniF2F-test 表示，每個子集包含 244 個問題，在主題領域中分布相同。我們保留 miniF2F 測試集專門用于評估模型性能，而 miniF2F 有效問題通過子目標分解被納入課程學習。我們采用了 Wang 等 人（2025 年） 發布的 miniF2F 修訂版，并進一步引入了 miniF2F-valid 的另外兩個版本和 miniF2F-test 的一個版本（見附錄 C）。

與 SoTA 模型的比較。

表1總結了在miniF2F-test數據集上評估的最新形式定理證明模型的對比情況。實驗結果表明，DeepSeek-Prover-V2-671B 在miniF2F-test基準測試中建立了新的最佳性能，僅利用32個樣本便實現了前所未有的82.4%的準確率，同時采用CoT生成策略。值得注意的是，參數效率更高的DeepSeek-Prover-V2-7B 也表現出競爭性的性能，超越了文獻中所有現有的開源定理證明器。進一步的比較分析揭示了一個引人注目的擴展模式：隨著樣本預算從1增加到8192，7B和671B變體之間的性能差距顯著擴大，較大的模型顯示出了更好的樣本效率和更陡峭的改進趨勢。

表 1：與 miniF2F-test 數據集上的最新模型對比。
符號 𝜇 ± 𝜎 表示平均準確率 𝜇 和標準差 𝜎。標簽 CoT 和 non-CoT 分別指代統一模型的兩種生成模式，每種模式由不同的提示引導。

通過子目標引導的課程來證明具有挑戰性的問題。

表2 詳細列出了DeepSeek-Prover-V2在miniF2F基準測試中解決的問題，它在驗證集上以91.0%的正確率和測試集上以88.9%的正確率實現了強整體性能。值得注意的是，我們所采用的子目標引導的課程學習框架，該框架將通用模型DeepSeek-V3與輕量級專門7B證明器相結合，實現了miniF2F-valid上90.2%的成功率，幾乎與DeepSeek-Prover-V2-671B的性能相匹配。這些發現突顯了當前最先進的通用LLM不僅能夠超越自然語言理解，還能夠在支持復雜形式推理任務方面發揮有效作用。通過戰略性地分解子目標，模型能夠將具有挑戰性的問題分解為一系列可處理的步驟，從而在非形式推理和形式證明構建之間架起一座有效橋梁。

表2: DeepSeek-Prover-V2-671B 在miniF2F基準測試中解決的問題。
miniF2F-valid上的結果是在課程學習過程中收集的，而對剩余的問題，則進一步使用Pass@8192調用DeepSeek-Prover-V2-671B。

基于推理 vs. 不基于推理。

表1中的實驗結果表明，在形式數學推理方面，基于推理的推理模式在性能上遠超無基于推理模式。這進一步證實了基于推理（CoT）提示的有效性，這種提示鼓勵將復雜問題分解為中間步驟，并進一步確認了推理時間縮放在形式定理證明領域中的有效性。補充這些發現，表3提供了DeepSeek-Prover-V2在不同推理模式下生成的令牌數量統計數據。正如預期的那樣，基于推理模式生成了顯著更長的輸出，反映出其復雜的推理過程。有趣的是，在無基于推理模式下，671B模型平均生成的輸出比7B模型更長。進一步檢查發現，雖然在無基于推理模式下沒有提示顯式的推理，但較大的模型往往在證明代碼中插入了一些類似于隱式推理步驟的簡要自然語言注釋（見附錄A）。這表明高容量模型即使在沒有顯式的基于推理提示的情況下，也可能隱式地內化并外化中間的推理過程。

表3：DeepSeek-Prover-V2 在 miniF2F-test 上生成的平均 Token 數量

3.2. 學士學位水平基準測試

ProofNet（Azerbayev等人，2023）包含371個問題，均基于Lean 3語言，這些問題來自各種流行的本科純數學教科書，涵蓋了實分析、復分析、線性代數、抽象代數和拓撲學等主題。我們使用Xin等人（2024b）提供的ProofNet的Lean 4翻譯版本，該版本進一步分為兩個部分：ProofNet-valid和ProofNet-test，分別包含185和186個問題。ProofNet的測試集專門用于模型評估，因為ProofNet-valid問題的變體包括在Dong和Ma（2025）提供的公共合成數據集中，該數據集用于我們的監督微調。如表4所示，與無基于推理（non-CoT）設置相比，使用基于推理（CoT）推理時DeepSeek-Prover-V2的通過率顯著提高。值得注意的是，盡管訓練數據主要來自高中水平的數學，該模型仍能很好地泛化到更高級的本科數學問題，這突顯了其強大的形式推理能力。

PutnamBench

PutnamBench（Tsoukalas等人，2024）是一個不斷更新的基準工具，包含從1962年至2023年的威廉·洛厄爾·普特南數學競賽中的競賽數學問題。普特南競賽是一個高度 prestigio 的年度數學競賽，面向美國和加拿大大學本科生，涵蓋分析、線性代數、抽象代數、組合數學、概率和集合論等多個大學水平的領域。我們評估了最新版本的PutnamBench，其中包含658個形式化化在Lean 4中的問題。排除與Lean 4.9.0不兼容的問題后，我們評估了剩余的649個問題。如表4所示，DeepSeek-Prover-V2-671B 在PutnamBench 中顯示出增強的推理能力，解決了49個問題，并顯著領先于其非基于推理（non-CoT）的版本。這些結果進一步突顯了基于推理（CoT）推理方法在處理有挑戰性的本科數學問題上的有效性。

表 4：ProofNet-test 和 PutnamBench 上的實驗結果。
PutnamBench 上 Goedel-Prover-SFT 和 STP 的分數來自他們的原始論文，該論文對包含 644 個問題的早期版本的 PutnamBench 進行了評估。

通過強化學習實現技能發現。

我們在評估中一個出乎意料的發現是，DeepSeek-Prover-V2-7B 在非基于推理（non-CoT）生成模式下在PutnamBench數據集中表現出色。值得注意的是，這個較小的7B模型成功解決了普特南Bench-671B未能解決的13個問題，使我們在普特南Bench中解決的問題總數從49個增加到62個，占658個總問題的百分比。經過仔細檢查模型的輸出，我們發現7B模型推理方法中的一種獨特模式：7B模型頻繁使用Cardinal.toNat和Cardinal.natCast_inj 來處理涉及有限基數的問題（見附錄B中的例子），而在671B版本生成的輸出中這些特定的技術幾乎是不存在的。這種方法似乎使模型能夠有效解決需要精妙操作基數值的問題的子集。

3.3 組合問題的結果

CombiBench

CombiBench（Liu等人，2025）是一個全面的基準工具，包含100個形式化化在Lean 4中的組合數學競賽問題，每個問題都配有相應的自然語言陳述。我們評估了DeepSeek-Prover-V2 在此基準中的有解設置，其中正確答案嵌入在Lean陳述中，使得評估主要集中在證明生成上。在過濾掉與Lean 4.9.0不兼容的問題以及包含多個“sorry”占位符的問題后，我們在基準中評估了77個問題，并成功解決了其中12個。這些結果表明，盡管證明模型主要是在數論和代數領域進行訓練的，但它在組合問題上展現出了令人鼓舞的泛化能力，盡管這類問題仍具持續的挑戰性。

3.4 ProverBench：AIME和教科書問題的形式化化

為了增強現有的基準并推進形式化化定理證明的研究，我們引入了一個包含325個問題的基準數據集。其中，15個問題是從最近的AIME競賽（AIME 24和25）中的數論和代數題目形式化化而來的，提供了真實的高中競賽級別挑戰。剩余的310個問題則來自精心挑選的教科書范例和教育教程，貢獻了一個多樣化且具有教學基礎的形式化化數學問題集合。此基準旨在能夠對高中競賽問題和大學級別數學進行全面評估。


AIME 形式化化。

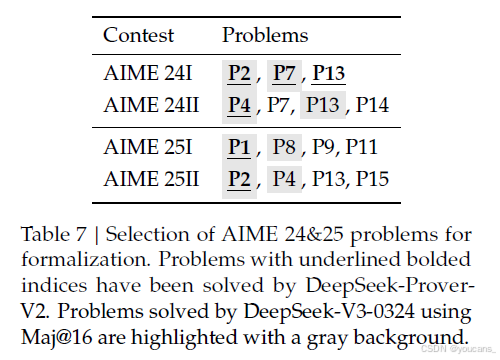
美國邀請數學考試（AIME）是一項每年舉行的數學競賽，旨在挑戰和表彰在數學表現出卓越能力的才華橫溢的高中學生。AIME 24 和 25 的題目已成為評估大型語言模型推理能力的標準基準。

為了彌合形式化化和非形式化化數學推理評估之間的差距，我們從 AIME 24 和 25 中精心挑選并形式化化了一部分問題。為了確保形式化化更簡潔，我們過濾掉了幾何、組合和計數問題，這些問題是 Lean 中難以處理的。這最終篩選出了 15 個選定問題，涵蓋了初等數論和代數的競賽級別主題。我們使用標準的“找答案”任務來評估 DeepSeek-V3-0324 在自然語言數學推理方面的性能。通過對 16 個抽樣響應進行多數投票，模型成功解決了 8 個問題。相比之下，DeepSeek-Prover-V2-671B 在給定正確答案的形式化化證明生成設置下，能夠為 6 個問題構建有效的形式證明。這一對比表明，非形式化化數學推理與形式化化定理證明之間的性能差距正在顯著縮小，顯示出高級語言模型在語言理解與形式邏輯 rigor 方面的逐步趨同。

教科書形式化化。

除了 AIME 24 和 25 題目外，我們還從用于高中競賽和本科課程的教科書中精心挑選了一些題目，以加強特定數學領域的內容覆蓋面。這一篩選過程確保了從易到難、從具體主題到廣泛領域的全面代表性。因此，我們形式化化了 310 個問題，涵蓋了廣泛的領域，從競賽水平的初等數學到通常在本科研究中遇到的高級主題。這一綜合性基準涵蓋了數論、初等代數、線性代數、抽象代數、微積分、實分析、復分析、泛函分析和概率。這種多樣化的數學領域包括的刻意選擇使得模型可以在不同抽象級別和推理風格上得到徹底評估。數論和代數問題測試模型處理離散結構和方程的能力，而分析傾向的問題則評估模型對極限、連續性以及微積分的理解。抽象代數和泛函分析部分的題目要求模型對抽象結構和空間進行推理，這需要高級的形式推理能力。評估結果詳見表 6。如表所示，具有 CoT 推理的 DeepSeek-Prover-V2-671B 一貫優于所有基線方法，這與之前其他基準評估中的觀察趨勢一致。

表6：ProverBench 的實驗結果。
All 類別代表包含325個問題的完整評估集，而AIME 24&25 表示從最近的AIME競賽中形式化化得出的15個問題的子集。STP（Dong和Ma，2025）的結果是使用開源模型權重進行評估的。

4. 結論

在本文中，我們提出了一個綜合的流程，用于生成冷啟動推理數據，以促進形式定理證明的發展。

我們的數據構建過程基于遞歸定理證明框架，在該框架中，DeepSeek-V3 作為統一模型，用于 Lean 4 證明助手內的子目標分解和引理形式化化。我們的方法結合了高層次的證明草圖和形式步驟，形成了一串可管理的子目標序列，這些子目標可以使用更小的 7B 模型高效解決，從而顯著減少了計算需求。

我們開發的學習課程框架利用這些分解的子目標生成更難的訓練任務，從而創建更有效的學習進度。通過將完整的形式證明與 DeepSeek-V3 的鏈式推理相結合，我們建立了有價值的冷啟動推理數據，將非形式化化的數學思考與形式證明結構聯系起來。隨后的強化學習階段顯著加強了這一聯系，導致形式定理證明能力有了顯著提升。

最終生成的模型 DeepSeek-Prover-V2-671B 在一系列基準測試中（涵蓋高中競賽題目和本科數學）一貫優于所有基線方法。

我們未來的工作將側重于將這一范式擴展到類似于 AlphaProof 的系統，最終目標是解決代表自動定理證明挑戰前沿的國際數學 Olympiad（IMO）級別的數學問題。

5. DeepSeek-Prover-V2 模型使用

5.1 模型與數據集下載

我們發布了兩種參數規模的 DeepSeek-Prover-V2 模型：7B 和 671B 參數。DeepSeek-Prover-V2-671B 基于 DeepSeek-V3-Base 訓練。DeepSeek-Prover-V2-7B 以 DeepSeek-Prover-V1.5-Base 為基礎，并具有最大 32K 詞元的擴展上下文長度。

模型下載：*

• DeepSeek-Prover-V2-7B：huggingface

• DeepSeek-Prover-V2-671B：huggingface

數據集下載：

DeepSeek-ProverBench：huggingface

5.2 快速入門

你可以直接使用 Huggingface 的 Transformers進行模型推理。DeepSeek-Prover-V2-671B 與 DeepSeek-V3 具有相同的架構。如需詳細信息和支持的功能，請參閱 Hugging Face 上的 DeepSeek-V3 文檔。

以下是從 miniF2F 數據集生成問題證明的一個基本示例：

from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
torch.manual_seed(30)model_id = "DeepSeek-Prover-V2-7B"  # or DeepSeek-Prover-V2-671B
tokenizer = AutoTokenizer.from_pretrained(model_id)formal_statement = """
import Mathlib
import Aesopset_option maxHeartbeats 0open BigOperators Real Nat Topology Rat/-- What is the positive difference between $120\%$ of 30 and $130\%$ of 20? Show that it is 10.-/
theorem mathd_algebra_10 : abs ((120 : ?) / 100 * 30 - 130 / 100 * 20) = 10 := bysorry
""".strip()prompt = """
Complete the following Lean 4 code:\```lean4
{}
\```Before producing the Lean 4 code to formally prove the given theorem, provide a detailed proof plan outlining the main proof steps and strategies.
The plan should highlight key ideas, intermediate lemmas, and proof structures that will guide the construction of the final formal proof.
""".strip()chat = [{"role": "user", "content": prompt.format(formal_statement)},
]model = AutoModelForCausalLM.from_pretrained(model_id, device_map="auto", torch_dtype=torch.bfloat16, trust_remote_code=True)
inputs = tokenizer.apply_chat_template(chat, tokenize=True, add_generation_prompt=True, return_tensors="pt").to(model.device)import time
start = time.time()
outputs = model.generate(inputs, max_new_tokens=8192)
print(tokenizer.batch_decode(outputs))
print(time.time() - start)

參考文獻

Azerbayev, Z., Piotrowski, B., Schoelkopf, H., Ayers, E. W., Radev, D., & Avigad, J. (2023). ProofNet: Autoformalizing and formally proving undergraduate-level mathematics. arXiv preprint arXiv:2302.12433.
Barras, B., Boutin, S., Cornes, C., Courant, J., Coscoy, Y., Delahaye, D., de Rauglaudre, D., Filliatre, J.-C., Giménez, E., Herbelin, H., et al. (1999). The Coq proof assistant reference manual. INRIA, version, 6(11), 17–21.
Barto, A. G., & Mahadevan, S. (2003). Recent advances in hierarchical reinforcement learning. Discrete Event Dynamic Systems, 13, 341–379.
DeepMind. (2024). AI achieves silver-medal standard solving international mathematical olympiad problems. Retrieved from https://deepmind.google/discover/blog/ai-solves-imo-problems-at-silver-medal-level/
DeepSeek-AI. (2024). Deepseek-v3 technical report. Retrieved from https://arxiv.org/abs/2412.19437
DeepSeek-AI. (2025). Deepseek-r1: Incentivizing reasoning capability in llms via reinforcement learning. Retrieved from https://arxiv.org/abs/2501.12948
Dong, K., & Ma, T. (2025). STP: Self-play llm theorem provers with iterative conjecturing and proving. arXiv preprint arXiv:2502.00212.
Dong, K., Mahankali, A., & Ma, T. (2024). Formal theorem proving by rewarding llms to decompose proofs hierarchically. arXiv preprint arXiv:2411.01829.
Eppe, M., Gumbsch, C., Kerzel, M., Nguyen, P. D., Butz, M. V., & Wermter, S. (2022). Intelligent problem-solving as integrated hierarchical reinforcement learning. Nature Machine Intelligence, 4(1), 11–20.
Hendrycks, D., Burns, C., Kadavath, A., Arora, A., Basart, S., Tang, E., Song, D., & Steinhardt, J. (2021). Measuring mathematical problem solving with the MATH dataset. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2).
Jaech, A., Kalai, A., Lerer, A., Richardson, A., El-Kishky, A., Low, A., Helyar, A., Madry, A., Beutel, A., Carney, A., et al. (2024). Openai o1 system card. arXiv preprint arXiv:2412.16720.
Jiang, A. Q., Welleck, S., Zhou, J. P., Lacroix, T., Liu, J., Li, W., Jamnik, M., Lample, G., & Wu, Y. (2023). Draft, sketch, and prove: Guiding formal theorem provers with informal proofs. In The Eleventh International Conference on Learning Representations.
Lample, G., Lachaux, M.-A., Lavril, T., Martinet, X., Hayat, A., Ebner, A., Rodriguez, A., & Lacroix, T. (2022). Hypertree proof search for neural theorem proving. In Proceedings of the 36th International Conference on Neural Information Processing Systems (pp. 26337–26349).
Li, Y., Du, D., Song, L., Li, C., Wang, W., Yang, T., & Mi, H. (2024). Hunyuanprover: A scalable data synthesis framework and guided tree search for automated theorem proving. arXiv preprint arXiv:2412.20735.
Lin, Y., Tang, S., Lyu, B., Wu, J., Lin, H., Yang, K., Li, J., Xia, M., Chen, D., Arora, S., et al. (2025). Goedel-Prover: A frontier model for open-source automated theorem proving. arXiv preprint arXiv:2502.07640.
Liu, J., Lin, X., Bayer, J., Dillies, Y., Jiang, W., Liang, X., Soletskyi, R., Wang, H., Xie, Y., Xiong, B., et al. (2025). CombiBench: Benchmarking llm capability for combinatorial mathematics. Retrieved from https://moonshotai.github.io/CombiBench/
Moura, L. d., & Ullrich, S. (2021). The Lean 4 theorem prover and programming language. In Automated Deduction–CADE 28: 28th International Conference on Automated Deduction, Virtual Event, July 12–15, 2021, Proceedings 28 (pp. 625–635). Springer.
Nachum, O., Gu, S. S., Lee, H., & Levine, S. (2018). Data-efficient hierarchical reinforcement learning. Advances in Neural Information Processing Systems, 31.
Paulson, L. C. (1994). Isabelle a Generic Theorem Prover. Springer Verlag.
Polu, S., & Sutskever, I. (2020). Generative language modeling for automated theorem proving. arXiv preprint arXiv:2009.03393.
Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
Shao, Z., Wang, P., Zhu, Q., Xu, R., Song, J., Zhang, M., Li, Y., Wu, Y., & Guo, D. (2024). DeepSeekMath: Pushing the limits of mathematical reasoning in open language models. arXiv preprint arXiv:2402.03300.
Tsoukalas, G., Lee, J., Jennings, J., Xin, J., Ding, M., Jennings, M., Thakur, A., & Chaudhuri, S. (2024). PutnamBench: Evaluating neural theorem-provers on the putnam mathematical competition. In The Thirty-eight Conference on Neural Information Processing Systems Datasets and Benchmarks Track.
Wang, H., Xin, H., Liu, Z., Li, W., Huang, Y., Lu, J., Zhicheng, Y., Tang, J., Yin, J., Li, Z., et al. (2024a). Proving theorems recursively. In The Thirty-eighth Annual Conference on Neural Information Processing Systems.
Wang, H., Xin, H., Zheng, C., Liu, Z., Cao, Q., Huang, Y., Xiong, J., Shi, H., Xie, E., Yin, J., et al. (2024b). Lego-prover: Neural theorem proving with growing libraries. In The Twelfth International Conference on Learning Representations.
Wang, H., Unsal, M., Lin, X., Baksys, M., Liu, J., Santos, M. D., Sung, F., Vinyes, M., Ying, Z., Zhu, Z., et al. (2025). Kimina-Prover Preview: Towards large formal reasoning models with reinforcement learning. arXiv preprint arXiv:2504.11354.
Wu, Z., Huang, S., Zhou, Z., Ying, H., Wang, J., Lin, D., & Chen, K. (2024). Internlm2.5-stepprover: Advancing automated theorem proving via expert iteration on large-scale lean problems. arXiv preprint arXiv:2410.15700.
Xin, H., Guo, D., Shao, Z., Ren, Z., Zhu, Q., Liu, B., Ruan, C., Li, W., & Liang, X. (2024a). DeepSeek-Prover: Advancing theorem proving in llms through large-scale synthetic data. arXiv preprint arXiv:2405.14333.
Xin, H., Ren, Z., Song, J., Shao, Z., Zhao, W., Wang, H., Liu, B., Zhang, L., Lu, X., Du, Q., et al. (2024b). DeepSeek-Prover-V1.5: Harnessing proof assistant feedback for reinforcement learning and monte-carlo tree search. arXiv preprint arXiv:2408.08152.
Xin, R., Xi, C., Yang, J., Chen, F., Wu, H., Xiao, X., Sun, Y., Zheng, S., & Shen, K. (2025). BFS-Prover: Scalable best-first tree search for llm-based automatic theorem proving. arXiv preprint arXiv:2502.03438.
Yang, K., Poesia, G., He, J., Li, W., Lauter, K., Chaudhuri, S., & Song, D. (2024). Formal mathematical reasoning: A new frontier in AI. arXiv preprint arXiv:2412.16075.
Ying, H., Wu, Z., Geng, Y., Wang, J., Lin, D., & Chen, K. (2024). Lean workbook: A large-scale lean problem set formalized from natural language math problems. In The Thirty-eight Conference on Neural Information Processing Systems Datasets and Benchmarks Track.
Zhang, J., Wang, Q., Ji, X., Liu, Y., Yue, Y., Zhang, F., Zhang, D., Zhou, G., & Gai, K. (2025). Leanabell-prover: Posttraining scaling in formal reasoning. arXiv preprint arXiv:2504.06122.
Zhao, X., Li, W., & Kong, L. (2023). Decomposing the enigma: Subgoal-based demonstration learning for formal theorem proving. arXiv preprint arXiv:2305.16366.
Zhao, X., Zheng, L., Bo, H., Hu, C., Thakker, U., & Kong, L. (2024). Subgoalxl: Subgoal-based expert learning for theorem proving. arXiv preprint arXiv:2408.11172.
Zheng, C., Wang, H., Xie, E., Liu, Z., Sun, J., Xin, H., Shen, J., Li, Z., & Li, Y. (2024). Lyra: Orchestrating dual correction in automated theorem proving. Transactions on Machine Learning Research.
Zheng, K., Han, J. M., & Polu, S. (2022). miniF2F: a cross-system benchmark for formal olympiad-level mathematics. In International Conference on Learning Representations.

版權聲明：
本文由 youcans@xidian 對論文 DeepSeek-Prover-V2: Advancing Formal Mathematical Reasoning via Reinforcement Learning for Subgoal Decomposition 進行摘編和翻譯，只供研究學習使用。

youcans@xidian 作品，轉載必須標注原文鏈接：
【DeepSeek論文精讀】12. DeepSeek-Prover-V2: 通過強化學習實現子目標分解的形式化化數學推理
Copyright 2025 youcans, XIDIAN
Created：2025-05