圖
圖(Graph)G由兩個集合V和E組成,記為:G=(V,E),其中V是頂點的有窮非空集合(其實就是頂點),E是V 中頂點偶對的有窮集合(就是邊)。V(G)和E(G)通常分別表示圖G的頂點集合以及邊集合,E(G)可以為空集合,但是此時的圖只有頂點,沒有邊。
舉個例子:
一個地圖: 頂點:城市 邊:路 可能只有城市沒有路就是E(G)可以為空集合,圖只有頂點,沒有邊。
多個城市 a b c d e
a 到b的方法(a到其他) :a - b a -c - b a - c - d - b
到a也有很多方法 b-a c-b-a 這樣就形成了網狀結構
1. 圖的分類
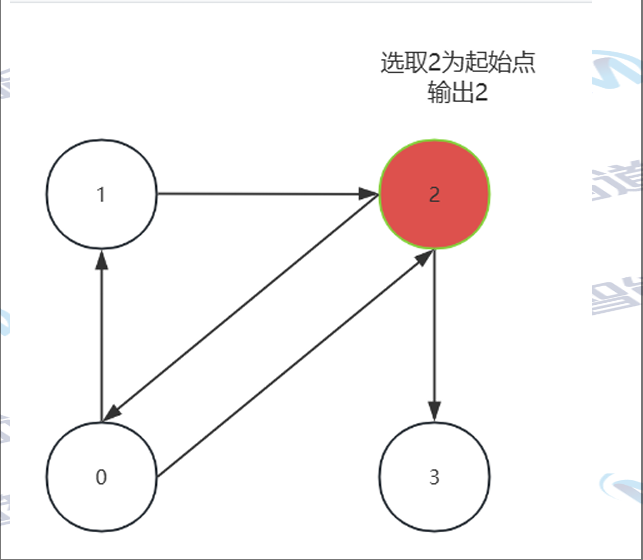
- 有向圖:
邊是有方向的。類似車道的單行道
這意味著每條邊都從一個頂點指向另一個頂點,并且這種指向關系是有序的,有向圖的 那個方向的線條稱為弧。在有向圖中,如果有一條從頂點A到頂點B的邊,那么我們說A指向B(A是起點,B是終點),但這并不 意味著B也指向A
示例
- 無向圖:
邊沒有方向。這意味著每條邊都連接兩個頂點,但不區分起點和終點。在無向圖中,如果兩個頂點由一 條邊連接,那么它們是相鄰的,并且這種相鄰關系是對稱的。
示例

- 網(帶權圖)
如果在圖的每條邊(或者弧)都被賦予一個權重(常用于表示節點之間連接的成本或距離),即為網 (帶權圖)

頂點的度
表示與頂點相連的邊的數量。
- 無向圖

- 有向圖
在有向圖中,頂點的度分為入度(In-degree)和出度(Out-degree)。
入度:指向該頂點的邊的數量。
出度:從該頂點出發的邊的數量。

- 路徑
圖的路徑是指由圖中的頂點和邊所構成的序列,其中頂點之間通過邊相連。
兩個頂點之間存在路徑(到達方式),說明它們是連通。
路徑可以是有向的或無向 的,這取決于圖的類型。

a->c連通 c->a不是因為 這是有向圖c到a沒有路徑到達
若任意兩個頂點之間都是連通的話,則圖是連通圖。

這就是聯通圖
- 鄰接點
鄰接點的定義是:如果兩個頂點之間存在一條邊,那么這兩個頂點就互為鄰接點
2 圖的存儲
2.1 鄰接矩陣
矩陣(二維數組)
鄰接矩陣是表示頂點間相鄰關系的矩陣。
對于n個頂點的圖,鄰接矩陣是一個n×n的二維數組(只存儲0 1)。兩個頂點存在直接連接到邊就是1,否則是0,自己到自己一般也是0
在無向圖中,鄰接矩陣是對稱的(對于對角線對稱),而在有向圖中則不一定。
-
- 無向圖

對應的鄰接矩陣是
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 1 |
| 2 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 1 | 1 | 0 | 0 |
- ?
- 有向圖

對應的鄰接矩陣是
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 |
代碼如下:
- 有向圖:
#include <iostream>
using namespace std;#define MAX_VERTICES 100 // 最大定點數// 初始化鄰接矩陣 int(*p)[MAX_VERTICES]也可以數組指針
void initalizeGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){adjMartix[i][j] = 0; // 初始化為0,表示沒有邊}}
}// 添加有向邊
void addDirectedEdge(int adjMartix[MAX_VERTICES][MAX_VERTICES], int u, int v) // uv是出度也是入度
{// 兩目標直接連接 有向圖adjMartix[u][v] = 1;// // 無向圖// adjMartix[v][u] = 1;
}
void printGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){printf("%d ", adjMartix[i][j]); // 初始化為0,表示沒有邊}printf("\n");}
}
// 打印圖int main()
{int adjMartix[MAX_VERTICES][MAX_VERTICES]; // 圖// 節點int n = 5;// 初始化圖initalizeGraph(adjMartix, n);// 添加有向邊addDirectedEdge(adjMartix, 0, 1);addDirectedEdge(adjMartix, 1, 0);addDirectedEdge(adjMartix, 1, 4);addDirectedEdge(adjMartix, 4, 0);addDirectedEdge(adjMartix, 4, 2);addDirectedEdge(adjMartix, 3, 2);// 打印有向圖printGraph(adjMartix, n);return 0;
}無向圖:
#include <iostream>
using namespace std;#define MAX_VERTICES 100 // 最大定點數// 初始化鄰接矩陣 int(*p)[MAX_VERTICES]也可以數組指針
void initalizeGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){adjMartix[i][j] = 0; // 初始化為0,表示沒有邊}}
}// 添加有向邊
void addDirectedEdge(int adjMartix[MAX_VERTICES][MAX_VERTICES], int u, int v) // uv是出度也是入度
{// 兩目標直接連接 有向圖adjMartix[u][v] = 1;// // 無向圖adjMartix[v][u] = 1;
}
void printGraph(int adjMartix[MAX_VERTICES][MAX_VERTICES], int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){printf("%d ", adjMartix[i][j]); // 初始化為0,表示沒有邊}printf("\n");}
}
// 打印圖int main()
{int adjMartix[MAX_VERTICES][MAX_VERTICES]; // 圖// 節點int n = 5;// 初始化圖initalizeGraph(adjMartix, n);// 添加有向邊addDirectedEdge(adjMartix, 0, 1);addDirectedEdge(adjMartix, 0, 4);addDirectedEdge(adjMartix, 1, 4);addDirectedEdge(adjMartix, 5, 3);addDirectedEdge(adjMartix, 3, 4);// 打印有向圖printGraph(adjMartix, n);return 0;
}
優點:
編碼簡單,容易理解。
便于檢查圖中任意兩個頂點之間是否存在邊。
便于計算圖中頂點的度。
缺點:
對于稀疏圖,鄰接矩陣會浪費大量存儲空間,因為矩陣中的大部分元素都是0。
在進行圖的遍歷等操作時,可能需要遍歷整個矩陣,效率較低。
2.2 鄰接表
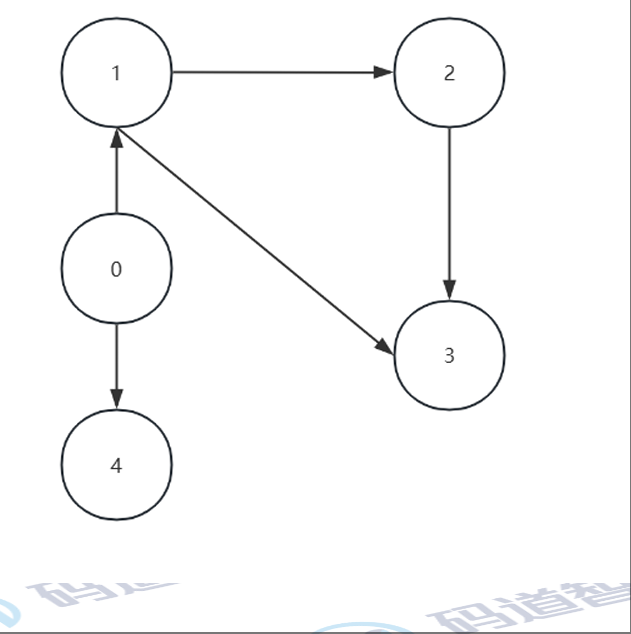
鄰接表是圖的一種鏈式存儲結構。對于圖中的每個頂點,鄰接表都存儲一個鏈表,該鏈表包含與該頂點相鄰的所有頂點。
例如下圖1包含和他相鄰的所有頂點,2和3
可以省略邊:連接關系2-3(隱含表示邊)(下節講,下面的代碼不省略)
1 - 2 - 3
1 - 3
代碼如下
#include <iostream>
using namespace std;// 定義邊
typedef struct EdgeNode
{int adjvex; // 鄰接點 終點struct EdgeNode *next; // 下一條邊 個指針用于連接同一起點的多條邊。這樣,我們就可以通// 過遍歷next指針來訪問從A出發的所有邊。
} EdgeNode;// 定義頂點
typedef struct VertexNode
{int data; // 起點信息EdgeNode *FirstNode; // 這個指針用于從頂點出發找到其第一條邊 。這樣,我們就可以從任意一// 個頂點開始,通過firstedge找到其所有鄰接點。
} VertexNode;typedef struct Grasp_List
{VertexNode *newNode; // 頂點int numVertices; // 頂點數int numEdges; // 邊數
} Grasp_List;// 初始化函數
void InitGraph(Grasp_List *graph, int n)
{graph->newNode = new VertexNode[n](); // 分配內存 ()會進行初始化graph->numVertices = n; 頂點5graph->numEdges = 0; // 邊0for (int i = 0; i < n; i++){graph->newNode[i].data = i; // 初始化每個頂點的數據graph->newNode[i].FirstNode = nullptr; // 初始化第一條邊為空}
}// 向圖中添加邊 u起始頂點 v鄰接點
void AddEdge(Grasp_List *graph, int u, int v)
{// 創建邊EdgeNode *newEdgeNode = (EdgeNode *)malloc(sizeof(EdgeNode)); // 創建新邊節點// 分配失敗if (!newEdgeNode){perror("分配失敗");return;}newEdgeNode->adjvex = v; // 設置鄰接點 也就是終點// 插入 頭插法 把邊直接newEdgeNode->next = graph->newNode[u].FirstNode; // 下一條邊=原來的第一條邊graph->newNode[u].FirstNode = newEdgeNode; // 更新第一條邊graph->numEdges++; // 邊數加1如果是無向圖 還需要再添加一條邊// EdgeNode* newNodeV = (EdgeNode*)malloc(sizeof(EdgeNode)); // 創建新邊節點// if (!newNodeV)//{// printf("申請內存失敗\n");// exit(-1);// }// newNodeV->adjvex = u; // 設置鄰接點頭插法// newNodeV->next = G->adjList[v].firstedge; // 下一條邊 = 原來的第一條邊// G->adjList[v].firstedge = newNodeV; // 更新第一條邊
}// 打印鄰接表
void printGraph(Grasp_List *graph)
{if (graph == nullptr){cout << "我是空圖" << endl;return;}printf("Graph with %d vertices and %d edge:\n", graph->numVertices, graph->numEdges);// 根據定點數遍歷for (int i = 0; i < graph->numVertices; i++){printf("vertices %d: ", graph->newNode[i].data); // 打印頂點// 找到頂點第一條邊EdgeNode *p = graph->newNode[i].FirstNode; // 保存while (p){// 鄰接點printf(" %d", p->adjvex);// 下一條邊p = p->next;}printf("\n");}
}// 釋放圖占用的內存
void freeGraph(Grasp_List *graph)
{if (graph == NULL){return;}// 釋放邊內存for (int i = 0; i < graph->numVertices; i++){EdgeNode *curerent = graph->newNode[i].FirstNode;EdgeNode *tmp = nullptr;while (curerent){tmp = curerent;curerent = curerent->next;free(tmp);tmp = nullptr;}curerent = nullptr;}// 釋放頂點內存delete[] (graph->newNode);graph->newNode = nullptr;// 釋放圖本身的內存delete graph;
}// 主函數實例
int main()
{Grasp_List *G = new Grasp_List;// 初始化圖InitGraph(G, 5);// 添加邊AddEdge(G, 0, 1);AddEdge(G, 0, 4);AddEdge(G, 1, 2);AddEdge(G, 1, 3);AddEdge(G, 2, 3);// 打印圖printGraph(G);// 釋放圖freeGraph(G);return 0;
}解釋一個遍創建的過程
AddEdge(G, 0, 1);
-
這表示在圖
G中添加一條從頂點0到頂點1的邊。 -
具體步驟如下:
- 創建一個新邊節點
newEdgeNode,并為其分配內存。 - 將新邊的鄰接點設置為
1。 - 使用頭插法將新邊插入到頂點
0的邊鏈表中,使新邊成為頂點0的第一條邊。 - 圖的邊數增加 1
- 創建一個新邊節點
-
形成鏈表的過程
在調用
AddEdge(G, 0, 1)后,頂點0和頂點1通過一條邊連接起來。具體來說:- 頂點
0的邊鏈表中新增了一個邊節點,其adjvex字段為1。 - 這個邊節點通過
next指針連接到原來頂點0的邊鏈表
- 頂點
優點:
節省存儲空間,特別是對于稀疏圖。
便于添加和刪除邊。
便于進行圖的遍歷等操作。
缺點:
不便于檢查圖中任意兩個頂點之間是否存在邊(需要遍歷兩個頂點的鄰接表)。
在某些情況下,可能需要額外的空間來存儲頂點的信息(如頂點的索引或名稱)。
和易損性(Vulnerability)在R中實現)







)


)


:Linux權限管理)




