1 排序算法；

1.1 如何分析一個排序算法

復雜度分析是整個算法學習的精髓。

• 時間復雜度: 一個算法執行所耗費的時間。
• 空間復雜度: 運行完一個程序所需內存的大小。

學習排序算法，我們除了學習它的算法原理、代碼實現之外，更重要的是要學會如何評價、分析一個排序算法。
分析一個排序算法，要從 執行效率、內存消耗、穩定性 三方面入手。

1.1.1 執行效率

1. 最好情況、最壞情況、平均情況時間復雜度

   我們在分析排序算法的時間復雜度時，要分別給出最好情況、最壞情況、平均情況下的時間復雜度。

2. 時間復雜度的系數、常數 、低階

   我們知道，時間復雜度 O（n）表示的是n很大的時候，所以它表示的時候會忽略系數、常數、低階。
   但是實際的軟件開發中，如果我們排序的可能是 10 個、100 個、1000 個這樣規模很小的數據，我們就要把系數、常數、低階也考慮進來。

3. 比較次數和交換（或移動）次數

   基于比較的排序算法的執行過程，會涉及兩種操作，一種是元素比較大小，另一種是元素交換或移動。
   所以，如果我們在分析排序算法的執行效率的時候，應該把比較次數和交換（或移動）次數也考慮進去。

3.1.2 內存消耗

也就是看空間復雜度。
還需要知道如下術語：

• 內排序：所有排序操作都在內存中完成；
• 外排序：由于數據太大，因此把數據放在磁盤中，而排序通過磁盤和內存的數據傳輸才能進行；
• 原地排序：原地排序算法，就是特指空間復雜度是 O(1) 的排序算法。

1.1.3 穩定性

• 穩定：如果待排序的序列中存在值相等的元素，經過排序之后，相等元素之間原有的先后順序不變。
  比如： a 原本在 b 前面，而 a = b，排序之后，a 仍然在 b 的前面；
• 不穩定：如果待排序的序列中存在值相等的元素，經過排序之后，相等元素之間原有的先后順序改變。
  比如：a 原本在 b 的前面，而 a = b，排序之后， a 在 b 的后面；

1.2 冒泡排序（Bubble Sort）

思想

• 冒泡排序只會操作相鄰的兩個數據。
• 每次冒泡操作都會對相鄰的兩個元素進行比較，看是否滿足大小關系要求。如果不滿足就讓它倆互換。
• 一次冒泡會讓至少一個元素移動到它應該在的位置，重復 n 次，就完成了 n 個數據的排序工作。

特點

• 優點：排序算法的基礎，簡單實用易于理解。
• 缺點：比較次數多，效率較低。

實現
（實現前先構思一遍場景）

// 冒泡排序
const bubbleSort=arr=>{let i,j;for(i=0;i<arr.length-1;i++){let hasChange=falsefor(j=0;j<arr.length-i-1;j++){if(arr[j]>arr[j+1]){let temp=arr[j+1]arr[j+1]=arr[j]arr[j]=temphasChange=true}}console.log('每輪排序',arr)if(!hasChange){break}}console.log('排序完成',arr)
}
//測試
let arr=[3,6,0,2,43,56,12,45,67]
console.log('初始值',arr)
bubbleSort(arr)

實現

1. 冒泡排序是原地排序算法嗎 ?
   冒泡的過程只涉及相鄰數據的交換操作，只需要常量級的臨時空間，所以它的空間復雜度為 O(1)，是一個原地排序算法。
2. 冒泡排序是穩定的排序算法嗎 ？
   在冒泡排序中，只有交換才可以改變兩個元素的前后順序。
   為了保證冒泡排序算法的穩定性，當有相鄰的兩個元素大小相等的時候，我們不做交換，相同大小的數據在排序前后不會改變順序。
   所以冒泡排序是穩定的排序算法。
3. 冒泡排序的時間復雜度是多少 ？
   最佳情況：T(n) = O(n)，當數據已經是正序時。
   最差情況：T(n) = O(n(2))，當數據是反序時。
   平均情況：T(n) = O(n(2))。

1.3 插入排序（Insertion Sort）

思想

一般人打撲克牌，整理牌的時候，都是按牌的大小（從小到大或者從大到小）整理牌的，那每摸一張新牌，就掃描自己的牌，把新牌插入到相應的位置。
插入排序的工作原理：通過構建有序序列，對于未排序數據，在已排序序列中從后向前掃描，找到相應位置并插入。

步驟

• 從第一個元素開始，該元素可以認為已經被排序；
• 取出下一個元素，在已經排序的元素序列中從后向前掃描；
• 如果該元素（已排序）大于新元素，將該元素移到下一位置；
• 重復步驟 3，直到找到已排序的元素小于或者等于新元素的位置；
• 將新元素插入到該位置后；
• 重復步驟 2 ~ 5。

實現

（實現前先構思一遍場景）

const insertionSort= arr=>{let i,j;for(i=1;i<arr.length;i++){let insertIndex=i;let insertItem=arr[i];for(j=i-1;j>=0;j--){if(insertItem<arr[j]){insertIndex=jarr[j+1]=arr[j]}else{//沒有比前面的小，就結束了break}}arr[insertIndex]=insertItemconsole.log('每輪排序',arr)}console.log('排序完成',arr)
}
//測試
let arr=[3,1,0,2,43,56,12,45,67]
console.log('初始值',arr)
insertionSort(arr)

分析

1. 插入排序是原地排序算法嗎
   插入排序算法的運行并不需要額外的存儲空間，所以空間復雜度是 O(1)，所以，這是一個原地排序算法。
2. 插入排序是穩定的排序算法嗎 ？
   在插入排序中，對于值相同的元素，我們可以選擇將后面出現的元素，插入到前面出現元素的后面，這樣就可以保持原有的前后順序不變，所以插入排序是穩定的排序算法。
3. 插入排序的時間復雜度是多少 ？
   最佳情況：T(n) = O(n)，當數據已經是正序時。
   最差情況：T(n) = O(n(2))，當數據是反序時。
   平均情況：T(n) = O(n(2))。

優化插入排序 – 拆半插入

折半插入排序是直接插入排序的升級版，鑒于插入排序第一部分為已排好序的數組，我們不必按順序依次尋找插入點，只需比較它們的中間值與待插入元素的大小即可。

拆半插入步驟

• 取 0 ~ i-1 的中間點 ( m = (i-1) >> 1 )，array[i] 與 array[m] 進行比較，若 array[i] < array[m]，則說明待插入的元素 array[i] 應該處于數組的 0 ~ m 索引之間；反之，則說明它應該處于數組的 m ~ i-1 索引之間。
• 重復步驟 1，每次縮小一半的查找范圍，直至找到插入的位置。
• 將數組中插入位置之后的元素全部后移一位。
• 在指定位置插入第 i 個元素。

注：x >> 1 是位運算中的右移運算，表示右移一位，等同于 x 除以 2 再取整，即 x >> 1 == Math.floor(x/2) ，可以自己實現

1.4 選擇排序（Selection Sort）

思路
選擇排序算法的實現思路有點類似插入排序，也分已排序區間和未排序區間。但是選擇排序每次會從未排序區間中找到最小的元素，將其放到已排序區間的末尾。
步驟

1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
2. 再從剩余未排序元素中繼續尋找最小（大）元素，然后放到已排序序列的末尾。
3. 重復第二步，直到所有元素均排序完畢。

實現

const selectionSort= arr=>{let i,j;for(i=0;i<arr.length-1;i++){//假設當前位置是最小值let minIndex=i;let tempt=arr[i];for(j=i+1;j<arr.length;j++){if(arr[j]<tempt){tempt=arr[j]minIndex=j}}//交換值arr[minIndex]=arr[i];arr[i]=temptconsole.log('每輪排序',arr)}console.log('排序完成',arr)
}
//測試
let arr=[3,1,0,2,43,56,12,45,67]
console.log('初始值',arr)
selectionSort(arr)

分析

1. 選擇排序是原地排序算法嗎 ？
   選擇排序空間復雜度為 O(1)，是一種原地排序算法。
2. 選擇排序是穩定的排序算法嗎 ？
   選擇排序每次都要找剩余未排序元素中的最小值，并和前面的元素交換位置，這樣破壞了穩定性。所以，選擇排序是一種不穩定的排序算法。
3. 選擇排序的時間復雜度是多少 ？
   無論是正序還是逆序，選擇排序都會遍歷 n(2) / 2 次來排序，所以，最佳、最差和平均的復雜度是一樣的。
   最佳情況：T(n) = O(n(2))。
   最差情況：T(n) = O(n(2))。
   平均情況：T(n) = O(n(2))。

1.5 歸并排序（Merge Sort）

思想
排序一個數組，我們先把數組從中間分成前后兩部分，然后對前后兩部分分別排序，再將排好序的兩部分合并在一起，這樣整個數組就都有序了。
歸并排序采用的是分治思想。
分治，顧名思義，就是分而治之，將一個大問題分解成小的子問題來解決。小的子問題解決了，大問題也就解決了。

實現

const mergeSort= arr=>{//向上取整和向下取整都可以let middleIndex=Math.floor(arr.length/2) let preArr=arr.slice(0,middleIndex)let nextArr=arr.slice(middleIndex)console.log('分割',preArr,nextArr)let newArr=[]if(preArr.length>2){//長度大于等于2的時候遞歸preArr=mergeSort(preArr)}else{if(preArr.length==2&&preArr[0]>preArr[1]){let temp=preArr[0]preArr[0]=preArr[1]preArr[1]=temp}console.log('前面的叔祖',preArr)}if(nextArr.length>2){//長度大于等于2的時候遞歸nextArr=mergeSort(nextArr)}else{if(nextArr.length==2&&nextArr[0]>nextArr[1]){let temp=nextArr[0]nextArr[0]=nextArr[1]nextArr[1]=temp}console.log('后面的叔祖',nextArr)}newArr=comparison(preArr,nextArr)console.log('每次返回',newArr)return newArr}//比較兩個有序的數組
const comparison=(arr1,arr2)=>{let newArr=[]while(arr1.length!=0&&arr2.length!=0){let aTempt=arr1[0]let bTempt=arr2[0]if(aTempt<=bTempt){ // 注意: 判斷的條件是小于或等于，如果只是小于，那么排序將不穩定.newArr.push(aTempt)arr1.shift()}else{newArr.push(bTempt)arr2.shift()}}if(arr1.length==0){newArr=newArr.concat(arr2)}if(arr2.length==0){newArr=newArr.concat(arr1)}return newArr
}
//測試
let arr=[3,1,7,3,8,88,90,76,0,2,43,56,12,45,67]
console.log('初始值',arr)
mergeSort(arr)

更標準的寫法

const mergeSort = arr => {//采用自上而下的遞歸方法const len = arr.length;if (len < 2) {return arr;}// length >> 1 和 Math.floor(len / 2) 等價let middle = Math.floor(len / 2),left = arr.slice(0, middle),right = arr.slice(middle); // 拆分為兩個子數組return merge(mergeSort(left), mergeSort(right));
};const merge = (left, right) => {const result = [];while (left.length && right.length) {// 注意: 判斷的條件是小于或等于，如果只是小于，那么排序將不穩定.if (left[0] <= right[0]) {result.push(left.shift());} else {result.push(right.shift());}}while (left.length) result.push(left.shift());while (right.length) result.push(right.shift());return result;
};

1. 歸并排序是原地排序算法嗎 ？
   這是因為歸并排序的合并函數，在合并兩個有序數組為一個有序數組時，需要借助額外的存儲空間。
   實際上，盡管每次合并操作都需要申請額外的內存空間，但在合并完成之后，臨時開辟的內存空間就被釋放掉了。在任意時刻，CPU 只會有一個函數在執行，也就只會有一個臨時的內存空間在使用。臨時內存空間最大也不會超過 n 個數據的大小，所以空間復雜度是 O(n)。
   所以，歸并排序不是原地排序算法。
2. 歸并排序是穩定的排序算法嗎 ？
   merge 方法里面的 left[0] <= right[0] ，保證了值相同的元素，在合并前后的先后順序不變。歸并排序是穩定的排序方法。
3. 歸并排序的時間復雜度是多少 ？
   從效率上看，歸并排序可算是排序算法中的佼佼者。假設數組長度為 n，那么拆分數組共需 logn 步，又每步都是一個普通的合并子數組的過程，時間復雜度為 O(n)，故其綜合時間復雜度為 O(n log n)。
   最佳情況：T(n) = O(n log n)。
   最差情況：T(n) = O(n log n)。
   平均情況：T(n) = O(n log n)。

1.6 快速排序（Quick Sort）

快速排序的特點就是快，而且效率高！它是處理大數據最快的排序算法之一。
思想

• 先找到一個基準點（一般指數組的中部），然后數組被該基準點分為兩部分，依次與該基準點數據比較，如果比它小，放左邊；反之，放右邊。
• 左右分別用一個空數組去存儲比較后的數據。
• 最后遞歸執行上述操作，直到數組長度 <= 1;
  特點：快速，常用。
  缺點：需要另外聲明兩個數組，浪費了內存空間資源。
  實現
  方法一：

const quickSort = arr=>{if(arr.length<2){return arr}let leftArr=[]let rightArr=[]let baseItem=arr[0]for(let i=1;i<arr.length;i++){let element=arr[i]if(element<=baseItem){leftArr.push(element)}else{rightArr.push(element)}}let newLeftArr = quickSort(leftArr)let newRightArr = quickSort(rightArr)let newArr=[...newLeftArr,baseItem,...newRightArr]console.log('每輪',newArr)return newArr}
//測試
let arr=[3,1,7,3,8,88,90,76,0,2,43,56,12,45,67]
console.log('初始值',arr)
console.log('排序后',quickSort(arr))

方法二：

const quickSort2 = (arr, left, right) => {let len = arr.length,partitionIndex;left = typeof left != 'number' ? 0 : left;right = typeof right != 'number' ? len - 1 : right;if (left < right) {partitionIndex = partition(arr, left, right);quickSort2(arr, left, partitionIndex - 1);quickSort2(arr, partitionIndex + 1, right);}return arr;
};const partition = (arr, left, right) => {//分區操作let pivot = left, //設定基準值（pivot）index = pivot + 1;for (let i = index; i <= right; i++) {if (arr[i] < arr[pivot]) {swap(arr, i, index);index++;}}swap(arr, pivot, index - 1);return index - 1;
};const swap = (arr, i, j) => {let temp = arr[i];arr[i] = arr[j];arr[j] = temp;
};
// 測試
const array = [3,1,7,3,8,88,90,76,0,2,43,56,12,45,67];
console.log('原始array:', array);
const newArr = quickSort2(array);
console.log('newArr:', newArr);

1. 快速排序是原地排序算法嗎 ？
   用方法二進行分區時，不需要很多額外的內存空間，所以快排是原地排序算法。
2. 快速排序是穩定的排序算法嗎 ？
   和選擇排序相似，快速排序每次交換的元素都有可能不是相鄰的，因此它有可能打破原來值為相同的元素之間的順序。因此，快速排序并不穩定。
3. 快速排序的時間復雜度是多少 ？
   極端的例子：如果數組中的數據原來已經是有序的了，比如 1，3，5，6，8。如果我們每次選擇最后一個元素作為 pivot，那每次分區得到的兩個區間都是不均等的。我們需要進行大約 n 次分區操作，才能完成快排的整個過程。每次分區我們平均要掃描大約 n / 2 個元素，這種情況下，快排的時間復雜度就從 O(nlogn) 退化成了 O(n(2))。
   最佳情況：T(n) = O(n log n)。
   最差情況：T(n) = O(n(2))。
   平均情況：T(n) = O(n log n)。

問題回答
快排和歸并用的都是分治思想，遞推公式和遞歸代碼也非常相似，那它們的區別在哪里呢 ？

可以發現：

• 歸并排序的處理過程是由下而上的，先處理子問題，然后再合并。
• 而快排正好相反，它的處理過程是由上而下的，先分區，然后再處理子問題。
• 歸并排序雖然是穩定的、時間復雜度為 O(nlogn) 的排序算法，但是它是非原地排序算法。
• 歸并之所以是非原地排序算法，主要原因是合并函數無法在原地執行。
• 快速排序通過設計巧妙的原地分區函數，可以實現原地排序，解決了歸并排序占用太多內存的問題。

1.7 希爾排序（Shell Sort）

思想

• 先將整個待排序的記錄序列分割成為若干子序列。
• 分別進行直接插入排序。
• 待整個序列中的記錄基本有序時，再對全體記錄進行依次直接插入排序。
  過程

1. 舉個易于理解的例子：[35, 33, 42, 10, 14, 19, 27, 44]，我們采取間隔 4。創建一個位于 4 個位置間隔的所有值的虛擬子列表。下面這些值是 { 35, 14 }，{ 33, 19 }，{ 42, 27 } 和 { 10, 44 }。
   

2. 我們比較每個子列表中的值，并在原始數組中交換它們（如果需要）。完成此步驟后，新數組應如下所示。
   

3. 然后，我們采用 2 的間隔，這個間隙產生兩個子列表：{ 14, 27, 35, 42 }， { 19, 10, 33, 44 }。
   

4. 我們比較并交換原始數組中的值（如果需要）。完成此步驟后，數組變成：[14, 10, 27, 19, 35, 33, 42, 44]，圖如下所示，10 與 19 的位置互換一下。
   

5. 最后，我們使用值間隔 1 對數組的其余部分進行排序，Shell sort 使用插入排序對數組進行排序。
   

實現

const shellSort = arr => {let len = arr.length,temp,gap = 1;console.time('希爾排序耗時');while (gap < len / 3) {//動態定義間隔序列gap = gap * 3 + 1;}for (gap; gap > 0; gap = Math.floor(gap / 3)) {for (let i = gap; i < len; i++) {temp = arr[i];let j = i - gap;for (; j >= 0 && arr[j] > temp; j -= gap) {arr[j + gap] = arr[j];}arr[j + gap] = temp;console.log('arr  :', arr);}}console.timeEnd('希爾排序耗時');return arr;
};

測試

// 測試
const array = [35, 33, 42, 10, 14, 19, 27, 44];
console.log('原始array:', array);
const newArr = shellSort(array);
console.log('newArr:', newArr);
// 原始 array:   [35, 33, 42, 10, 14, 19, 27, 44]
// arr      :   [14, 33, 42, 10, 35, 19, 27, 44]
// arr      :   [14, 19, 42, 10, 35, 33, 27, 44]
// arr      :   [14, 19, 27, 10, 35, 33, 42, 44]
// arr      :   [14, 19, 27, 10, 35, 33, 42, 44]
// arr      :   [14, 19, 27, 10, 35, 33, 42, 44]
// arr      :   [14, 19, 27, 10, 35, 33, 42, 44]
// arr      :   [10, 14, 19, 27, 35, 33, 42, 44]
// arr      :   [10, 14, 19, 27, 35, 33, 42, 44]
// arr      :   [10, 14, 19, 27, 33, 35, 42, 44]
// arr      :   [10, 14, 19, 27, 33, 35, 42, 44]
// arr      :   [10, 14, 19, 27, 33, 35, 42, 44]
// 希爾排序耗時: 3.592041015625ms
// newArr:     [10, 14, 19, 27, 33, 35, 42, 44]

分析

1. 希爾排序是原地排序算法嗎 ？
   希爾排序過程中，只涉及相鄰數據的交換操作，只需要常量級的臨時空間，空間復雜度為 O(1) 。所以，希爾排序是原地排序算法。
2. 希爾排序是穩定的排序算法嗎 ？
   我們知道，單次直接插入排序是穩定的，它不會改變相同元素之間的相對順序，但在多次不同的插入排序過程中，相同的元素可能在各自的插入排序中移動，可能導致相同元素相對順序發生變化。
   因此，希爾排序不穩定。
3. 希爾排序的時間復雜度是多少 ？
   最佳情況：T(n) = O(n log n)。
   最差情況：T(n) = O(n log(2) n)。
   平均情況：T(n) = O(n log(2) n)。

1.8 堆排序（Heap Sort）

堆的定義
堆其實是一種特殊的樹。只要滿足這兩點，它就是一個堆。

• 堆是一個完全二叉樹。
  完全二叉樹：除了最后一層，其他層的節點個數都是滿的，最后一層的節點都靠左排列。
• 堆中每一個節點的值都必須大于等于（或小于等于）其子樹中每個節點的值。
  也可以說：堆中每個節點的值都大于等于（或者小于等于）其左右子節點的值。這兩種表述是等價的。
  對于每個節點的值都大于等于子樹中每個節點值的堆，我們叫作大頂堆。
  對于每個節點的值都小于等于子樹中每個節點值的堆，我們叫作小頂堆。
  
  其中圖 1 和 圖 2 是大頂堆，圖 3 是小頂堆，圖 4 不是堆。除此之外，從圖中還可以看出來，對于同一組數據，我們可以構建多種不同形態的堆。
  思想

1. 將初始待排序關鍵字序列 (R1, R2 … Rn) 構建成大頂堆，此堆為初始的無序區；
2. 將堆頂元素 R[1] 與最后一個元素 R[n] 交換，此時得到新的無序區 (R1, R2, … Rn-1) 和新的有序區 (Rn) ，且滿足 R[1, 2 … n-1] <= R[n]。
3. 由于交換后新的堆頂 R[1] 可能違反堆的性質，因此需要對當前無序區 (R1, R2 … Rn-1) 調整為新堆，然后再次將 R[1] 與無序區最后一個元素交換，得到新的無序區 (R1, R2 … Rn-2) 和新的有序區 (Rn-1, Rn)。不斷重復此過程，直到有序區的元素個數為 n - 1，則整個排序過程完成。
   實現

// 堆排序
const heapSort = array => {console.time('堆排序耗時');// 初始化大頂堆，從第一個非葉子結點開始for (let i = Math.floor(array.length / 2 - 1); i >= 0; i--) {heapify(array, i, array.length);}// 排序，每一次 for 循環找出一個當前最大值，數組長度減一for (let i = Math.floor(array.length - 1); i > 0; i--) {// 根節點與最后一個節點交換swap(array, 0, i);// 從根節點開始調整，并且最后一個結點已經為當前最大值，不需要再參與比較，所以第三個參數為 i，即比較到最后一個結點前一個即可heapify(array, 0, i);}console.timeEnd('堆排序耗時');return array;
};// 交換兩個節點
const swap = (array, i, j) => {let temp = array[i];array[i] = array[j];array[j] = temp;
};// 將 i 結點以下的堆整理為大頂堆，注意這一步實現的基礎實際上是：
// 假設結點 i 以下的子堆已經是一個大頂堆，heapify 函數實現的
// 功能是實際上是：找到 結點 i 在包括結點 i 的堆中的正確位置。
// 后面將寫一個 for 循環，從第一個非葉子結點開始，對每一個非葉子結點
// 都執行 heapify 操作，所以就滿足了結點 i 以下的子堆已經是一大頂堆
const heapify = (array, i, length) => {let temp = array[i]; // 當前父節點// j < length 的目的是對結點 i 以下的結點全部做順序調整for (let j = 2 * i + 1; j < length; j = 2 * j + 1) {temp = array[i]; // 將 array[i] 取出，整個過程相當于找到 array[i] 應處于的位置if (j + 1 < length && array[j] < array[j + 1]) {j++; // 找到兩個孩子中較大的一個，再與父節點比較}if (temp < array[j]) {swap(array, i, j); // 如果父節點小于子節點:交換；否則跳出i = j; // 交換后，temp 的下標變為 j} else {break;}}
};

測試

const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
console.log('原始array:', array);
const newArr = heapSort(array);
console.log('newArr:', newArr);
// 原始 array:  [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
// 堆排序耗時: 0.15087890625ms
// newArr:     [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]

分析

1. 堆排序是原地排序算法嗎 ？
   整個堆排序的過程，都只需要極個別臨時存儲空間，所以堆排序是原地排序算法。
2. 堆排序是穩定的排序算法嗎 ？
   因為在排序的過程，存在將堆的最后一個節點跟堆頂節點互換的操作，所以就有可能改變值相同數據的原始相對順序。
   所以，堆排序是不穩定的排序算法。
3. 堆排序的時間復雜度是多少 ？
   堆排序包括建堆和排序兩個操作，建堆過程的時間復雜度是 O(n)，排序過程的時間復雜度是 O(nlogn)，所以，堆排序整體的時間復雜度是 O(nlogn)。
   最佳情況：T(n) = O(n log n)。
   最差情況：T(n) = O(n log n)。
   平均情況：T(n) = O(n log n)。

2 動態規劃和貪心算法；

2.1 動態規劃

遞歸是從頂部開始將問題分解，通過解決掉所有分解出小問題的方式，來解決整個問題。
動態規劃解決方案從底部開始解決問題，將所有小問題解決掉，然后合并成一個整體解決方案，從而解決掉整個大問題。
使用遞歸去解決問題雖然簡潔，但效率不高。

2.1.1 斐波拉契數列

斐波拉契數列定義為以下序列：

0，1，1，2，3，5，8，13，21，34，55，…

可以看到，當 n >= 2，a(n) = a(n - 1) + a(n - 2)。這個數列的歷史非常悠久，它是被公元700年一位意大利數學家斐波拉契用來描述在理想狀態下兔子的增長情況。
不難看出，這個數列可以用一個簡單的遞歸函數表示。

function fibo (n) {if (n <= 0)  return 0;if (n === 1) return 1;return fibo(n - 1) + fibo(n - 2);
}

這種實現方式非常耗性能，在n的數量級到達千級別，程序就變得特別慢，甚至失去響應。如果使用動態規劃從它能解決的最簡單子問題著手的話，效果就很不一樣了。
這里我們先用一個數組來存取每一次產生子問題的結果，方便后面求解使用。

function fibo (n) {if (n <= 0) return 0;if (n <= 1) return 1;var arr = [0, 1];for (var i = 2; i <= n; i++) {arr[i] = arr[i - 1] + arr[i - 2];}return arr[n];
}

這里的數組可以去掉，換做局部變量來實現可以省下不少內存空間。

function fibo (n) {if (n <= 0) return 0;if (n <= 1) return 1;var res, a = 0, b = 1;for (var i = 2; i <= n; i++) {res = a + b;a = b;b = res;}return res;
}

2.1.2 尋找最長公共子串

另一個適合使用動態規劃去解決的問題是尋找兩個字符串的最長公共子串。例如，在單詞 raven 和 havoc中，最長的公共子串是“av”。

function maxSubString (str1, str2) {if (!str1 || !str2) return '';var len1 = str1.length,len2 = str2.length;var maxSubStr = '';for (var i = 0; i < len1; i++) {for (var j = 0; j < len2; j++) {var tempStr = '',k = 0;while ((i + k < len1) && (j + k < len2) && (str1[i + k] === str2[j + k])) {tempStr += str1[i + k];k++;}if (tempStr.length >  maxSubStr.length) {maxSubStr = tempStr;}}}return maxSubStr;
}

2.1.3 背包問題

背包問題是算法研究中的一個經典問題。
你是一個保險箱大盜，打開了一個裝滿奇珍異寶的保險箱，但是你必須將這些寶貝放入你的一個小背包中。保險箱中的物品規格和價值不同。你希望自己的背包裝進的寶貝總價值最大。
當然，暴力計算可以解決這個問題，但是動態規劃會更為有效。使用動態規劃來解決背包問題的關鍵思路是計算裝入背包的每一個物品的最大價值，直到背包裝滿。
表1：0-1背包問題

物品	A	B	C	D	E
價值	4	5	10	11	13
尺寸	3	4	7	8	9

首先，我們看看遞歸方式怎么去解決這個問題：

function knapsack (capacity, objectArr, order) {if (order < 0 || capacity <= 0) {return 0;}if (arr[order].size > capacity) {return knapsack(capacity, objectArr, order - 1);}return Math.max(arr[order].value + knapsack(capacity - arr[order].size, objectArr, order - 1),knapsack(capacity, objectArr, order - 1));
}console.log(knapsack(16, [{value: 4, size: 3},{value: 5, size: 4},{value: 10, size: 7},{value: 11, size: 8},{value: 13, size: 9}
], 4)); // 23

為了提高程序的運行效率，我們不妨將遞歸實現方式改成動態規劃。
注意，理解0-1背包問題的突破口，就是要理解 “0-1” 這個含義，這里對于每一件物品，要么帶走（1），要么留下（0)。

基本思路

0-1背包問題子結構：選擇一個給定第 i 件物品，則需要比較選擇第 i 件物品的形成的子問題的最優解與不選擇第 i件物品的子問題的最優解。分成兩個子問題，進行選擇比較，選擇最優的。

若將 f[i][w] 表示前 i 件物品恰放入一個容量為 w 的背包可以獲得的最大價值。則其狀態轉移方程便是：

f[i][w] = max{ f[i-1][w], f[i-1][w-w[i]]+v[i] }

其中，w[i] 表示第 i 件物品的重量，v[i] 表示第 i 件物品的價值。

function knapsack (capacity, objectArr) {var n = objectArr.length;var f = [];for (var i = 0; i <= n; i++) {f[i] = [];for (var w = 0; w <= capacity; w++) {if (i === 0 || w === 0) {f[i][w] = 0;} else if (objectArr[i - 1].size <= w) {var size = objectArr[i - 1].size,value = objectArr[i - 1].valuef[i][w] = Math.max(f[i - 1][w - size] + value, f[i - 1][w]);} else {f[i][w] = f[i - 1][w];}}}return f[n][capacity];
}

2.2 貪心算法

前面研究的動態規劃算法，它可以用于優化通過次優算法找到的解決方案——這些方案通常是基于遞歸方案實現的。對許多問題來說，采用動態規劃的方式去處理有點大材小用，往往一個簡單的算法就夠了。
貪心算法就是一種比較簡單的算法。貪心算法總是會選擇當下的最優解，而不去考慮這一次的選擇會不會對未來的選擇造成影響。使用貪心算法通常表明，實現者希望做出的這一系列局部“最優”選擇能夠帶來最終的整體“最優”選擇。

2.2.1 背包問題

如果用到的物品是連續的，那么可以簡單地通過物品的單價除以單位體積來確定物品的價值。在這種情況下的最優 是，先裝價值最高的物品直到該物品裝完或者將背包裝滿，接著裝價值次高的物品，直到這種物品也裝完或將背包裝滿，以此類推。我們把這種問題類型叫做 “部分背包問題”。
表2：部分背包問題

物品	A	B	C	D	E
價值	50	140	60	60	80
尺寸	5	20	10	12	20
比率	10	7	6	5	4

我們不能通過貪心算法來解決離散物品問題的原因，是因為我們無法將“半臺電視”放入背包。換句話說，貪心算法不能解決0-1背包問題，因為在0-1背包問題下，你必須放入整個物品或者不放入。

比如，貪心算法計算出單位面積價值最高的物品，依次放入后，背包容量假設剩余10，下一個要放入的是B，尺寸為20，便放不下了。如果不是離散（單個整體物品）的，就可以放入部分填滿。

function knapsack (capacity, objectArr) {// 首先按性價比排序, 高 -> 低objectArr.sort(function (a, b) {return parseFloat(b.value / b.size) - parseFloat(a.value / a.size);});// 記錄物品個數var n = objectArr.length;// 記錄已經選中尺寸，已選最大的最大價值var selected = 0,maxValue = 0;for (var i = 0; i < n && selected < capacity; i++) {var size = objectArr[i].size,value = objectArr[i].value;if (size <= capacity - selected) {maxValue += value;selected += size;} else {// 計算比例maxValue += value * ((capacity - selected) / size);selected  = capacity;}}return maxValue;
}

3 樹；

3.1 樹

不同于我們上面介紹的線性結構，樹是一種非線性結構。
圖：

它遵循：

• 僅有唯一一個根節點，沒有節點則為空樹
• 除根節點外，每個節點都有并僅有唯一一個父節點
• 節點間不能形成閉環

樹有幾個概念：

• 擁有相同父節點的節點，互稱為兄弟節點
• 節點的深度 ：從根節點到該節點所經歷的邊的個數
• 節點的高度 ：節點到葉節點的最長路徑
• 樹的高度：根節點的高度
  
  B、C、D就互稱為兄弟節點，其中，節點B的高度為2，節點B的深度為 1，樹的高度為3

3.1.1 高度

樹的高度計算公式：

下圖每個節點值都代表來當前節點的高度：

3.2 二叉樹

二叉樹，故名思義，最多僅有兩個子節點的樹（最多能分兩個叉的樹）：

3.3 平衡二叉樹

二叉樹中，每一個節點的左右子樹的高度相差不能大于 1，稱為平衡二叉樹。

另外還有滿二叉樹、完全二叉樹等：

• 滿二叉樹：除了葉結點外每一個結點都有左右子葉且葉子結點都處在最底層的二叉樹
• 完全二叉樹：深度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第h 層所有的結點都連續集中在最左邊

3.4 在代碼中如何去表示一棵二叉樹

3.4.1 鏈式存儲法

二叉樹的存儲很簡單，在二叉樹中，我們看到每個節點都包含三部分：

• 當前節點的 val
• 左子節點 left
• 右子節點 right

所以我們可以將每個節點定義為：

function Node(val) {// 保存當前節點 key 值this.val = val// 指向左子節點this.left = null// 指向右子節點this.right = null
}

一棵二叉樹可以由根節點通過左右指針連接起來形成一個樹。

function BinaryTree() {let Node = function (val) {this.val = valthis.left = nullthis.right = null}let root = null
}

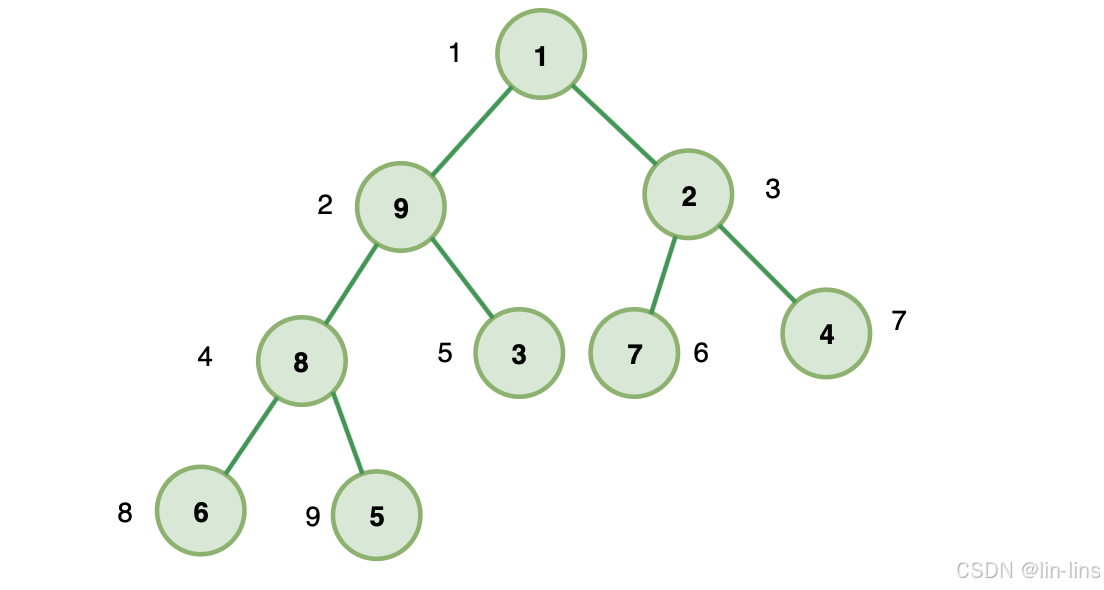
3.4.2 數組存儲法（適用于完全二叉樹）

下圖就是一棵完全二叉樹，
如果我們把根節點存放在位置 i=1 的位置，則它的左子節點位置為 2i = 2 ，右子節點位置為 2i+1 = 3 。
如果我們選取 B 節點 i=2 ，則它父節點為 i/2 = 1 ，左子節點 2i=4 ，右子節點 2i+1=5 。
以此類推，我們發現所有的節點都滿足這三種關系：

• 位置為 i 的節點，它的父節點位置為 i/2
• 它的左子節點 2i
• 它的右子節點 2i+1

因此，如果我們把完全二叉樹存儲在數組里（從下標為 1 開始存儲），我們完全可以通過下標找到任意節點的父子節點。從而完整的構建出這個完全二叉樹。這就是數組存儲法。
數組存儲法相對于鏈式存儲法不需要為每個節點創建它的左右指針，更為節省內存。

3.5 二叉樹的遍歷

二叉樹的遍歷可分為：

• 前序遍歷
• 中序遍歷
• 后序遍歷

所謂前、中、后，不過是根的順序，即也可以稱為先根遍歷、中根遍歷、后根遍歷

3.5.1 前序遍歷

對于二叉樹中的任意一個節點，先打印該節點，然后是它的左子樹，最后右子樹

3.5.2 中序遍歷

對于二叉樹中的任意一個節點，先打印它的左子樹，然后是該節點，最后右子樹

3.5.3 后序遍歷

對于二叉樹中的任意一個節點，先打印它的左子樹，然后是右子樹，最后該節點

3.5.4 代碼實現（前序遍歷為例）

所以，遍歷二叉樹的過程也就是一個遞歸的過程，例如前序遍歷，先遍歷根節點，然后是根的左子樹，最后右子樹；遍歷根節點的左子樹的時候，又是先遍歷左子樹的根節點，然后左子樹的左子樹，左子樹的右子樹…….
所以，它的遞歸實現就是：

遞歸實現

// 前序遍歷
var preorderTraversal = (root) => {let result = []var preOrderTraverseNode = (node) => {if(node) {// 先根節點result.push(node.val)// 然后遍歷左子樹preOrderTraverseNode(node.left)// 再遍歷右子樹preOrderTraverseNode(node.right)}}preOrderTraverseNode(root)return result
};

我們既然可以使用遞歸實現，那么是否也可以使用迭代實現？

迭代實現
利用棧來記錄遍歷的過程，實際上，遞歸就使用了調用棧，所以這里我們可以使用棧來模擬遞歸的過程

• 首先根入棧
• 將根節點出棧，將根節點值放入結果數組中
• 然后遍歷左子樹、右子樹，因為棧是先入后出，所以，我們先右子樹入棧，然后左子樹入棧
• 繼續出棧（左子樹被出棧）…….
  依次循環出棧遍歷入棧，直到棧為空，遍歷完成

// 前序遍歷
const preorderTraversal = (root) => {const list = [];const stack = [];// 當根節點不為空的時候，將根節點入棧if(root) stack.push(root)while(stack.length > 0) {const curNode = stack.pop()// 第一步的時候，先訪問的是根節點list.push(curNode.val)// 我們先打印左子樹，然后右子樹// 所以先加入棧的是右子樹，然后左子樹if(curNode.right !== null) {stack.push(curNode.right)}if(curNode.left !== null) {stack.push(curNode.left)}}return list
}

復雜度分析
空間復雜度：O(n)
時間復雜度：O(n)

4 DFS與BFS

• DFS：深度優先遍歷
• BFS：廣度優先遍歷

4.1 DFS（深度優先遍歷）

js實現該算法代碼(遞歸版本)：

function deepFirstSearch(node,nodeList) {  if (node) {    nodeList.push(node);    var children = node.children;    for (var i = 0; i < children.length; i++) //每次遞歸的時候將 需要遍歷的節點 和 節點所存儲的數組傳下去deepFirstSearch(children[i],nodeList);    }    return nodeList;  
} 

非遞歸版本：

function deepFirstSearch(node) {var nodes = [];if (node != null) {var stack = [];stack.push(node);while (stack.length != 0) {var item = stack.pop();nodes.push(item);var children = item.children;for (var i = children.length - 1; i >= 0; i--)stack.push(children[i]);}}return nodes;
}

4.2 BFS（廣度優先遍歷）

js實現算法代碼（遞歸版本）：

function breadthFirstSearch(node) {var nodes = [];var i = 0;if (!(node == null)) {nodes.push(node);breadthFirstSearch(node.nextElementSibling);node = nodes[i++];breadthFirstSearch(node.firstElementChild);}return nodes;
}

非遞歸版本：

function breadthFirstSearch(node) {  var nodes = [];  if (node != null) {  var queue = [];  queue.unshift(node);  while (queue.length != 0) {  var item = queue.shift();  nodes.push(item);  var children = item.children;  for (var i = 0; i < children.length; i++)  queue.push(children[i]);  }  }  return nodes;  
}