目錄
- 1 視線引導法介紹
- 2 LOS制導原理推導
- 3 Lyapunov穩定性分析
- 4 LOS制導效果
1 視線引導法介紹
視線引導法(Line of Sight, LOS)作為無人水面艇(USV)自主導航領域的核心技術,通過幾何制導與動態控制深度融合的機制,為復雜海洋環境下的高精度路徑跟蹤提供了魯棒性解決方案。其核心原理建立在運動學幾何投影與閉環反饋控制的雙重架構上:系統實時計算無人船當前位置與預設航路點之間的視線角,通過航向控制器動態調整船體艏搖角使其精確對準該視線方向,同時配合自適應航速策略,形成兼具軌跡跟蹤精度與運動穩定性的制導體系。

為實現視線角的精確跟蹤,LOS制導與航向控制器形成級聯控制架構:LOS制導系統首先根據全局路徑規劃生成的航路點序列構建虛擬參考路徑,在每個控制周期內選取距離船體最近的路徑點作為當前跟蹤目標,通過幾何投影建立船體坐標系與慣性坐標系間的空間映射關系,計算得到視線角 ψ l o s \psi_{los} ψlos?,從而生成期望航向指令 ψ d \psi_{d} ψd?,內環控制層則基于航向偏差 e ψ p ˉ s i d ? ψ e_\psi\=psi_{d}-\psi eψ?pˉ?sid??ψ,通過控制算法輸出轉艏力矩τ_r,驅動推進系統調整船體方向,如下圖所示

2 LOS制導原理推導
如圖所示為LOS制導幾何關系示意圖
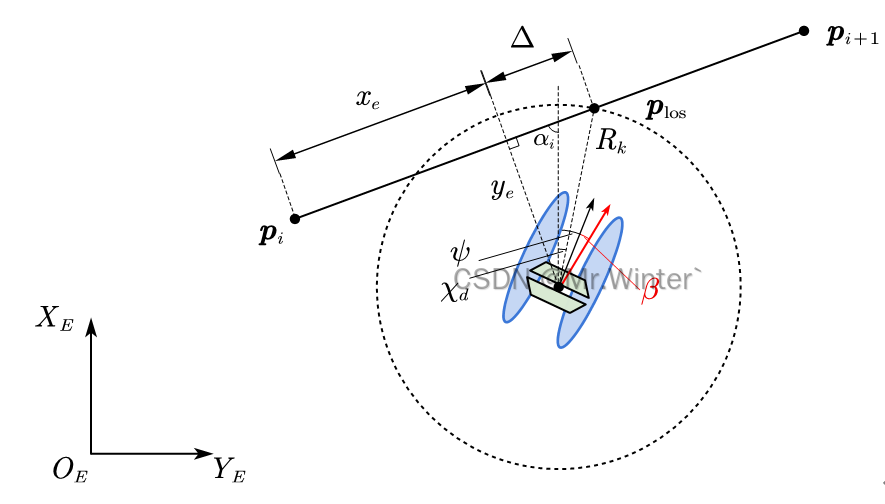
設上一個路點為 p i \boldsymbol{p}_i pi?,下一個路點為 p i + 1 \boldsymbol{p}_{i+1} pi+1?,USV當前位置為 p = [ x y ] T \boldsymbol{p}=\left[ \begin{matrix} x& y\\\end{matrix} \right] ^T p=[x?y?]T。以 p \boldsymbol{p} p為圓心作半徑為 R k R_k Rk?的圓交直線段 p i p i + 1 \boldsymbol{p}_i\boldsymbol{p}_{i+1} pi?pi+1?于兩點,距離下一個路點 p i + 1 \boldsymbol{p}_{i+1} pi+1?較近的交點為當前跟蹤的期望路點 p l o s \boldsymbol{p}_{\mathrm{los}} plos?。定義前視距離 Δ \Delta Δ為USV在當前段路徑投影點與LOS制導點 p l o s \boldsymbol{p}_{\mathrm{los}} plos?的前向距離,在靜態LOS制導律中, Δ \Delta Δ或 R k R_k Rk?為定值(已知 Δ \Delta Δ或 R k R_k Rk?中的一項可以求出另一項),一般設為USV長度 L L L的 n n n倍,即
Δ = n L \Delta =nL Δ=nL
由幾何關系可得橫縱向跟蹤誤差
{ x e = ( x ? x i ) cos ? α i + ( y ? y i ) sin ? α i y e = ? ( x ? x i ) sin ? α i + ( y ? y i ) cos ? α i \begin{cases} x_e=\left( x-x_i \right) \cos \alpha _i+\left( y-y_i \right) \sin \alpha _i\\ y_e=-\left( x-x_i \right) \sin \alpha _i+\left( y-y_i \right) \cos \alpha _i\\\end{cases} {xe?=(x?xi?)cosαi?+(y?yi?)sinαi?ye?=?(x?xi?)sinαi?+(y?yi?)cosαi??
其中 α i = a r c tan ? ( ( y i + 1 ? y i ) / ( x i + 1 ? x i ) ) \alpha _i=\mathrm{arc}\tan \left( {{\left( y_{i+1}-y_i \right)}/{\left( x_{i+1}-x_i \right)}} \right) αi?=arctan((yi+1??yi?)/(xi+1??xi?))。在USV運動過程中,受到風浪或自身驅動等因素影響將產生橫向速度 v v v,使船艏不一定沿著航向行駛,艏向和航向的差角稱為漂角
β = a r c tan ? ( v , u ) \beta =\mathrm{arc}\tan \left( v,u \right) β=arctan(v,u)
則USV當前航向角為 χ = ψ + β \chi =\psi +\beta χ=ψ+β,期望的航向角 χ d = α i ? a r c tan ? ( y e / Δ ) \chi _d=\alpha _i-\mathrm{arc}\tan \left( {{y_e}/{\Delta}} \right) χd?=αi??arctan(ye?/Δ),令 χ = χ d \chi =\chi _d χ=χd?可得
ψ d = α i ? a r c tan ? ( y e / Δ ) ? β \psi _d=\alpha _i-\mathrm{arc}\tan \left( {{y_e}/{\Delta}} \right) -\beta ψd?=αi??arctan(ye?/Δ)?β
即控制USV艏向為 ψ d \psi_d ψd?時可使其沿著期望航向運動
3 Lyapunov穩定性分析
下來驗證當采用 ψ = ψ d \psi=\psi_d ψ=ψd?制導時可使橫向誤差收斂為零。求橫向誤差的一階導數
y ˙ e = ? x ˙ sin ? α i + y ˙ cos ? α i \dot{y}_e=-\dot{x}\sin \alpha _i+\dot{y}\cos \alpha _i y˙?e?=?x˙sinαi?+y˙?cosαi?
根據運動學方程得到
y ˙ e = ? ( u cos ? ψ ? v sin ? ψ ) sin ? α i + ( u sin ? ψ + v cos ? ψ ) cos ? α i \dot{y}_e=-\left( u\cos \psi -v\sin \psi \right) \sin \alpha _i+\left( u\sin \psi +v\cos \psi \right) \cos \alpha _i y˙?e?=?(ucosψ?vsinψ)sinαi?+(usinψ+vcosψ)cosαi?
根據輔助角公式展開
y ˙ e = u 2 + v 2 sin ? ( ψ + β ? α i ) \dot{y}_e=\sqrt{u^2+v^2}\sin \left( \psi +\beta -\alpha _i \right) y˙?e?=u2+v2?sin(ψ+β?αi?)
代入LOS制導律
y ˙ e = u 2 + v 2 sin ? ( ? a r c tan ? ( y e / Δ ) ) = ? u 2 + v 2 y e Δ 2 + y e 2 \begin{aligned} \dot{y}_e&=\sqrt{u^2+v^2}\sin \left( -\mathrm{arc}\tan \left( {{y_e}/{\Delta}} \right) \right) \\ &=-\sqrt{u^2+v^2}\frac{y_e}{\sqrt{\Delta ^2+y_{e}^{2}}}\end{aligned} y˙?e??=u2+v2?sin(?arctan(ye?/Δ))=?u2+v2?Δ2+ye2??ye???
設Lyapunov函數
V = y e 2 2 V=\frac{y_{e}^{2}}{2} V=2ye2??
則
V ˙ = ? u 2 + v 2 y e 2 Δ 2 + y e 2 ? 0 \dot{V}=-\sqrt{u^2+v^2}\frac{y_{e}^{2}}{\sqrt{\Delta ^2+y_{e}^{2}}}\leqslant 0 V˙=?u2+v2?Δ2+ye2??ye2???0
根據Lyapunov第二判據可知橫向誤差在LOS制導律下漸進穩定。
4 LOS制導效果
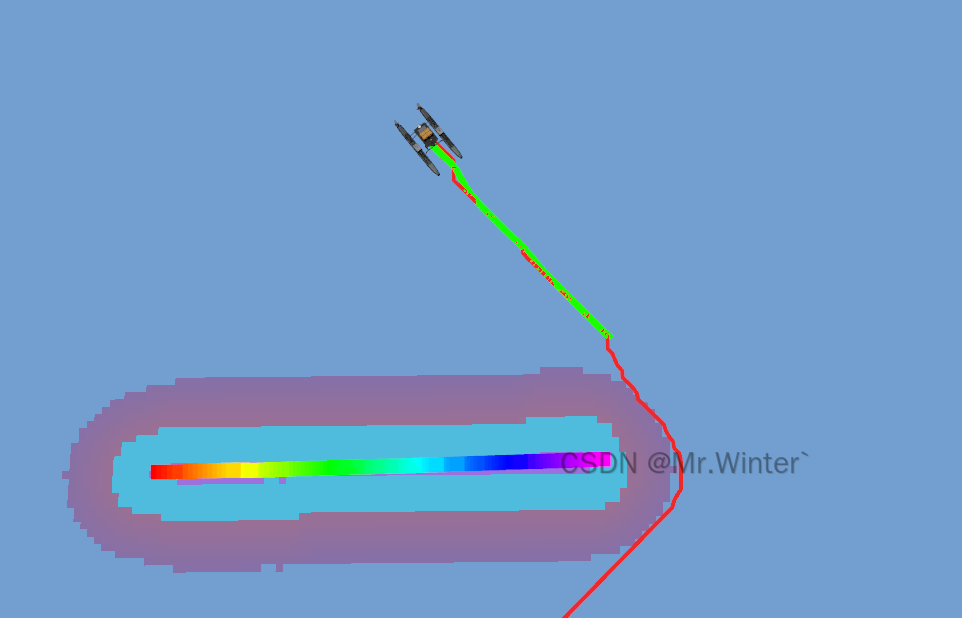
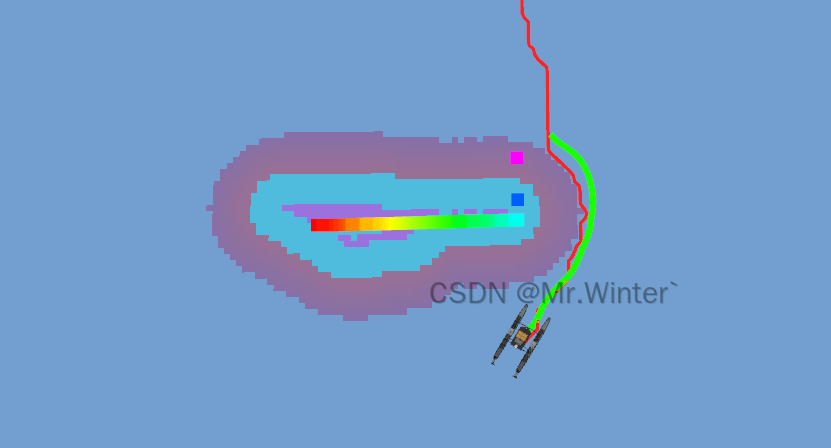
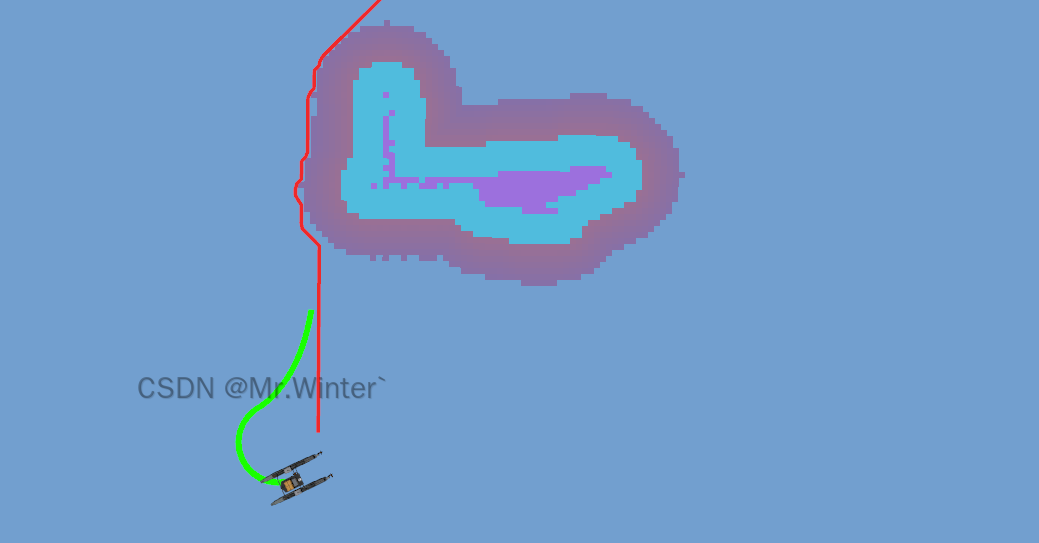
在下面的演示中,紅色的是全局路徑點,綠色的是LOS制導生成的模擬軌跡
🔥 更多精彩專欄:
- 《ROS從入門到精通》
- 《Pytorch深度學習實戰》
- 《機器學習強基計劃》
- 《運動規劃實戰精講》
- …








)




)



![[ctfshow web入門] web37](http://pic.xiahunao.cn/[ctfshow web入門] web37)

