智能車攝像頭開源—9 動態權、模糊PID、速度決策、路徑優化

一、前言

二、動態權

1.概述

2.偏差值加動態權

三、模糊PID

四、速度決策

?1.曲率計算

2.速度擬合

3.速度控制

五、路徑

六、國賽視頻

一、前言

? ? ? ? 在前中期通過識別直道、彎道等元素可進行加減速操作實現速度的控制，可進一步縮減一圈的運行速度，但會出現剎車不及時、加速不及時、車路徑較差等問題，反而導致處理后運行一圈時間反而多于之前。由此我們引入多個方法，使車輛能自行解算自行控制速度、轉向力度等，以跑出最好效果。

? ? ? ? 當然有部分代碼為了提高摩托運行穩定性的，對于四輪車模反而是一種限制，需讀者使用時自行刪減。

二、動態權

1.概述

? ? ? ?如果圖像有六十行，那我們可以得到六十行有效偏差值（彎道時有效行數會減少），我們在計算偏差值時，常用的方法是將所有有效行的偏差值相加，再取均值。

? ? ? ? 但調過車的都知道，當所有行取均值時，會導致彎道打角力度不夠，直線打角力度過大導致車輛擺動的情況。

? ? ? ? 參考我們平時開車或者騎車時的情形，車快時我們眼睛就看的遠，車速慢時我們眼睛就看的近。由此我們可以優化上述情況，引入加權。

? ? ? ? 最簡單且繁瑣的方法是引入固定權值（提前錄入權值數組），即提前設定好不同元素的加權情況：

? ? ? ? 1. 如識別出直線時，我們將圖像遠端的權值加大，而圖像中端和近端的權值減小，在遠端出現彎道時，會讓車輛高速情況下提前出現打角傾向。

? ? ? ? 2. 當貼近彎道時，我們將圖像中端的權值加大，就可以減少底端較小偏差值的干擾，保證車的打角力度。

? ? ? ? 3. 識別出小S彎時，我們將權值情況如同直線處理，高權值放在遠端，那么就可以驚奇的發現，車在跑小S彎時幾乎無左右擺動情況，直線路徑穿過小S彎，在提高車速的同時也減少了打角消耗的時間。

? ? ? ? 4. 在處理十字和環島時，我們可以對多個狀態設定權值，可以優化在元素不同狀態時的轉向效果。

? ? ? ? 但上述方法存在弊端：一方面元素與元素之間權值會切換的很生硬，使車輛出現擺動；另一方面當我們需要加速時，所有的元素權值都需要調整，十分繁瑣。由此我們引入動態權。

2.給偏差值加動態權

? ? ? ?控制動態權我們使用一個數據，為爬線相遇點的Y值（一個可以反映偏差值有效行的數據），那么在直線和小S彎等地方，Y貼近圖像最遠端，那么高權值就自動滑動到最遠端。在由直線靠近彎道時，相遇點Y值不斷下壓，那么高權值就隨著Y值向下滑動到中間區域，整個過程很絲滑，不會出現強硬的切換，并且十分易于修改。下面上代碼：

            //相遇點滑動均值濾波uint8 Y_Meet_Max = 0;uint8 Y_Meet_Min = 0;uint16 Y_Meet_Sum = 0;uint8 Y_Meet_Average = 0;Y_Meet_Min = Y_Meet_Array[0];Y_Meet_Max = Y_Meet_Array[0];for(i = 0; i < 19; i++){Y_Meet_Array[i + 1] = Y_Meet_Array[i];}Y_Meet_Array[0] = start;for(i = 0; i < 20; i++){if(Y_Meet_Array[i] < Y_Meet_Min){Y_Meet_Min = Y_Meet_Array[i];}if(Y_Meet_Array[i] > Y_Meet_Max){Y_Meet_Max = Y_Meet_Array[i];}}for(i = 0; i < 20; i++){Y_Meet_Sum += (uint16)Y_Meet_Array[i];}Y_Meet_Sum = Y_Meet_Sum - (uint16)Y_Meet_Min - (uint16)Y_Meet_Max;Y_Meet_Average = (uint8)(Y_Meet_Sum / 18);if(Y_Meet_Average > 20){Y_Meet_Average = 20;}else if(Y_Meet_Average < 2){Y_Meet_Average = 2;}   //一直到這里都是華東均值濾波，濾的比較狠，防止數據跳動//        float Temp_Float = (0.9f * (float)(Y_Meet_Average - 2) + 1.8f * Sensitivity);float Temp_Float = (float)(Y_Meet_Average - 2);     //當直線時，我的Y_Meet值是2if(Temp_Float > 18.0f)      //限幅{Temp_Float = 18.0f;}if(Temp_Float < 0){Temp_Float = 0;}//固定權值uint8 Base_Weight[60] = {0, 0, 2, 0, 2, 0, 2, 0, 2, 0,      2, 0, 2, 0, 2, 0, 2, 0, 2, 0,      2, 0, 2, 0, 2, 0, 2, 0, 2, 0,2, 0, 2, 0, 2, 0, 2, 0, 2, 0,      2, 0, 2, 0, 2, 0, 2, 0, 2, 0,      2, 0, 2, 0, 2, 0, 2, 1, 0, 0};//局部動態權值，可根據車速自行調整區間和數值uint8 Trends_Weight[19] = {4, 5, 5, 6, 6, 7, 7, 8, 9, 10, 9, 8, 7, 7, 6, 6, 5, 5, 4};//動態權重加權起始行只能落在24 - 40行之間(由下往上)，相遇點最大值為20（減2為Temp_Float最大值為18）uint8 Start_Line = (uint8)(Temp_Float / 18.0f * 16.0f + 24.0f);//將動態權值賦值給固定權值數組for(i = 0; i < 19; i ++){Base_Weight[Start_Line - i] = Trends_Weight[i];}for(i = Y_Meet_Average + 1; i < 57; i++)    //加權，可直接加權給中線之后再算偏差值，也可直接加權給每行偏差值{Sum += (int32)Base_Weight[i] * (int32)C_Line[i];Weight_Sum += (int32)Base_Weight[i];}

? ? ?? ?識別出元素時也可適當給固定權保證車輛行駛的穩定性。

三、模糊PID

????????模糊PID，是對P, I, D其中一個變量或幾個變量進行模糊，每模糊一個參數，就需要寫一個對應的模糊表。當模糊多個參數時，調參工作量會增大。因此我們組別只模糊了專項環的P值

? ? ? ? 模糊PID重要的是原理，先上一張圖：

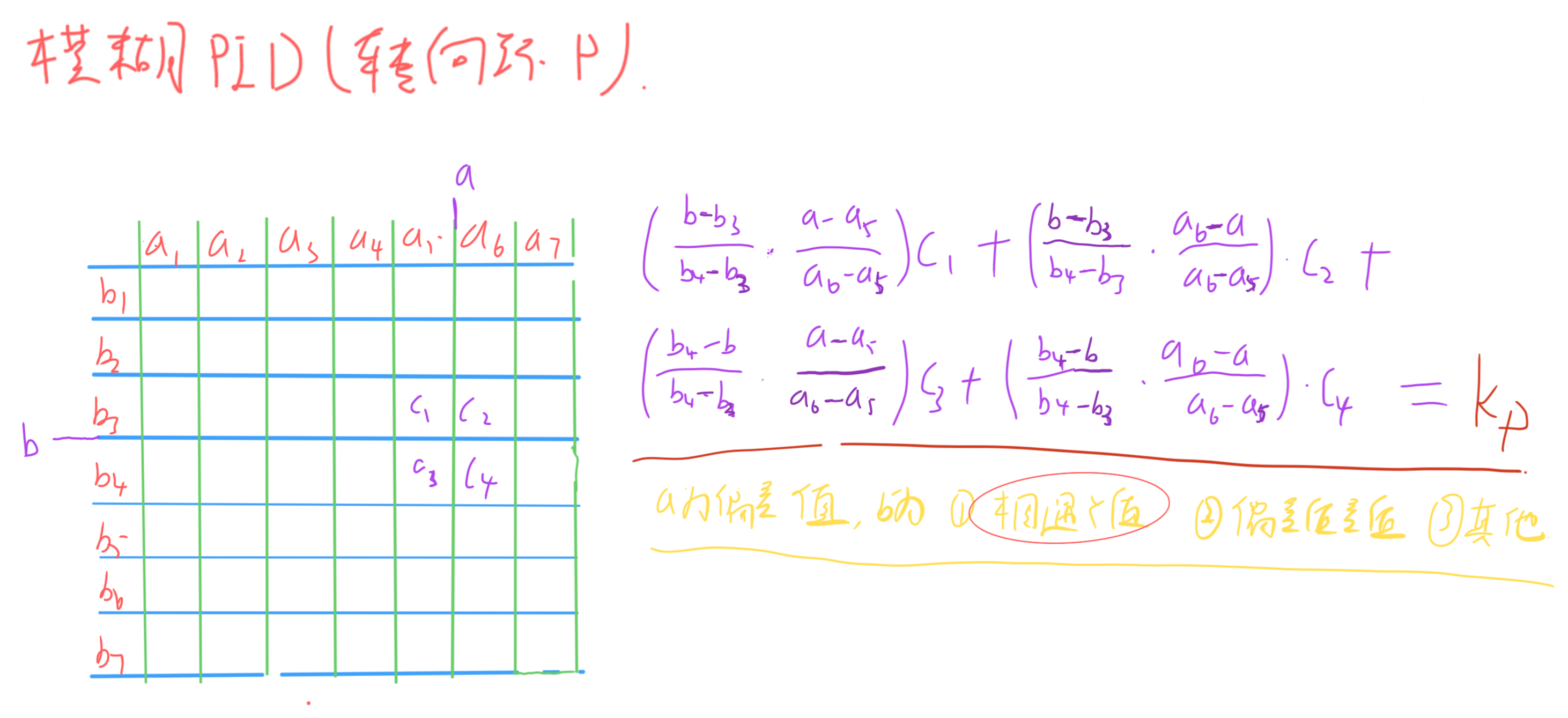
（自己手繪潦草勿噴）

? ? ? ?模糊的原理即查表映射，上述圖中，a為偏差值；b網絡上多為偏差值的差值，即偏差值的變化率（反映偏差值的變化情況，如直線時變化率很小，進入彎道時變化率會很大）；c就是對應的Kp值了。舉例理解：我的偏差值區間為 -1 到 1 （其中負數向左轉，正數向右轉），那么我將（-1,1）等分為六個區間（七個值），作為模糊表的橫向變量。列向變量也是同理。

? ? ? ? 那我們映射的時候，是獲得一個偏差值，再獲得一個偏差值的差值，然后在表中一查找直接對應到一個值作為轉向環的P嗎？

? ? ? ? 是也不是。我們會發現我們很少會獲得一個a參數和b參數，其中a參數和 a1~a7中的某一個值正好對應，b參數也正好和b1~b7中的某一個值正好對應，絕大多數情況下兩者是都無法正好相對的，那么我們就需使用占比對應的方式。

? ? ? ? 正如上述圖中的式子，假設我們獲得一個偏差a位于區間a5~a6，偏差的差值b位于區間b3~b4，那我們可列出如下式子：

Kp =? [(b - b3）/? (b4 - b3)] * [(a - a5) / (a6 - a5)] * c1 +

???????? [(b - b3）/? (b4 - b3)] * [(a6 - a) / (a6 - a5)] * c2?+

???????? [(b4 - b）/? (b4 - b3)] * [(a - a5) / (a6 - a5)] * c3?+

???????? [(b4 - b）/? (b4 - b3)] * [(a6 - a) / (a6 - a5)] * c4

? ? ? ? 不要覺得式子很長很繁瑣，就是初中的知識，一眼就能看懂。理解了上述原理后，就懂了模糊PID查表的核心思路。然后閱讀這篇文章（其中隸屬度通俗點講就是所占的比例，代碼可看可不看）：

【智能車】模糊PID控制原理詳解與代碼實現

? ? ? ? 然后我們再細說下c，即如何在表格中填入Kp的值：

? ? ? ? 1. 首先我們讓車以一個恒定速度行進，測出彎道轉向時需要的Kp值，即PB（盡量使路徑最好）；

? ? ? ? 2. 然后給一個較快的速度，測出直線時車身比較平穩的Kp值，即NB（盡量使路徑最好）；

? ? ? ? 3. 然后將最大~最小值均分為七個值，對應上述文章里的NB ~ PB；

? ? ? ? 4. 最后將Kp的七個值，按照既定的規則表填入表格內（注意不要自己亂填，當自己能力足夠時可自行優化規則表）

? ? ? ? 到這一步，相必已經完全了解模糊PID的原理和使用方法了，那么接下來就是代碼的實現了。這里代碼與上述方法相似但不相同，但核心原理與方法是完全一致的，只是實現的方式進行了改進。此處我的b使用的并不是偏差值的差值，而是爬線相遇點的Y值：

//除了注釋了（需要改）的地方，其他地方直接照抄就可以float Dif_Effictive_Line = 40.0f;    //偏差值最大值
int16 View_Effictive_Line = 20;      //相遇點Y坐標的最大值（需要改）float P_Value_L[7] = {11.0f, 12.0f, 12.5f, 13.0f, 14.5f, 15.5f, 17.2f};    //這里沒有等分，自己調一調車可摸出規律（需要改）float Vague_Array[4][4] = { {0, 1, 2, 3},{1, 2, 3, 4},{3, 4, 5, 6},{5, 6, 6, 6}};    //這個表原樣抄下來float f_Get_H_approximation(int16 i16_ViewH)     
{float H_approximation;if (i16_ViewH < 0){i16_ViewH = 0;}H_approximation = ((float)i16_ViewH * 3.0f / (float)View_Effictive_Line);    //*3.0是為了將結果放大三倍return H_approximation;
}float f_Get_E_approximation(float i16_E)
{float E_approximation;if (i16_E < 0){i16_E = -i16_E;}E_approximation = (float)i16_E * 40.0f * 3.0f/ Dif_Effictive_Line;    //*3.0與上述同理，還多乘了個四十，與Dif_Effictive_Line 的值對應上return E_approximation;
}int16 Off_Line = 0;
int16 Now_Off_Line = 0;    //用于濾波
int16 Last_Off_Line = 0;    //用于濾波第一個參數輸入相遇點Y坐標
第二個參數輸入歸一化后的偏差值
float Get_P(int16 off_line, float dif_value)
{Last_Off_Line = Now_Off_Line;Now_Off_Line = off_line;if(((Now_Off_Line - Last_Off_Line) >= 10) || ((Now_Off_Line - Last_Off_Line) <= -10) || Now_Off_Line >= 45)    //需要改{Off_Line = Last_Off_Line;}else{Off_Line = (int16)(0.3f * (float)(Now_Off_Line) + 0.7f * (float)(Last_Off_Line));}//下面這部分代入幾個數據，結合整段代碼計算幾遍即可理解，只看的話比較吃力float VH = f_Get_H_approximation(off_line - 2);float VE = f_Get_E_approximation(dif_value);float X2Y = 0;float X1Y = 0;float Y2X = 0;float Y1X = 0;int8 VH1 = (int)VH;if (VH1 > VH){VH--;}int8 VH2 = VH1 + 1;int8 VE1 = (int8)VE;if (VE1 > VE){VE1--;}int8 VE2 = VE1 + 1;if (VH1 > 3){VH1 = 3;}if (VH2 > 3){VH2 = 3;}if (VE1 > 3){VE1 = 3;}if (VE2 > 3){VE2 = 3;}X2Y = (Vague_Array[VH1][VE2] - Vague_Array[VH1][VE1]) * (VE - VE1) + Vague_Array[VH1][VE1];X1Y = (Vague_Array[VH2][VE2] - Vague_Array[VH2][VE1]) * (VE - VE1) + Vague_Array[VH2][VE1];Y2X = (Vague_Array[VH2][VE1] - Vague_Array[VH1][VE1]) * (VH - VH1) + Vague_Array[VH1][VE1];Y1X = (Vague_Array[VH2][VE2] - Vague_Array[VH1][VE2]) * (VH - VH1) + Vague_Array[VH1][VE2];float P_approximation = (X2Y + X1Y + Y2X + Y1X) / 4.0;int8 P1 = (int8)P_approximation;if (P1 > P_approximation){P1--;}int8 P2 = P1 + 1;return (P_Value_L[P2] - P_Value_L[P1]) * (P_approximation - P1) + P_Value_L[P1]; //返回p值
}

四、速度決策

?1.曲率計算

? ? ? ? 速度要變化起來，就需要有參考，即根據一個或兩個實時求出的數據去控制權值的滑動。那么第一個變量我使用的是中線曲率：

? ? ? ? 曲率我嘗試了很多算法，都不是很穩定，由此大道至簡，直接將中線每兩行之間的X坐標的差值相加求均值再歸一化（歸一化所除的系數在彎道處實測得出），就可以反映中線的彎曲程度，也近似可看為曲率。

? ? ? ? 注：這里每兩行之間X坐標的差值不可取絕對值后再相加。在彎道時，中線是向一側彎的，那么X坐標的差值的符號都是一樣的，可以得到一個比較大的均值。而在小S彎處，X坐標的差值有正有負，那么相加之后求均值會獲得一個比較小的值，這是將小S彎當直線處理的關鍵所在。

? ? ? ? 這里我的代碼參照動態權的思想給曲率的計算也加了個小型化的動態權，即突出重點區域，使用爬線相遇點Y坐標（即圖像最大有效行）控制權值移動，可自行修改這部分，根據實際情況選用是否需要這部分處理。

? ? ? ? 下面上代碼：

float Last_Curvature_Value = 0;     //防止
/**
* 函數功能：      計算中線曲率，作為控制速度的一個數據
* 特殊說明：      無
* 形  參：        uint8 *line      中線
*                 uint8 start      爬線相遇點的Y值，或最大有效行
*                 uint8 end        爬線起始行（或圖像最底端）
*
* 示例：          Calculate_Curvature_2(C_Line, Y_Meet, L_Start_Point[1]);
* 返回值：        Last_Curvature_Value      所得曲率
*/
float Calculate_Curvature_2(uint8 *line, uint8 start, uint8 end)
{int16 Sum_Difference_Value = 0;     //用于X坐標差值的累積int16 Sum_Weight = 0;               //用于權值相加uint8 i = 0;uint8 Base_Curvature_Weight[60] = {0, 0, 1, 0, 1, 0, 1, 0, 1, 0,1, 0, 1, 0, 1, 0, 1, 0, 1, 0,1, 0, 1, 0, 1, 0, 1, 0, 1, 0,1, 0, 1, 0, 1, 0, 1, 0, 1, 0,1, 0, 1, 0, 1, 0, 1, 0, 1, 0,1, 0, 1, 0, 1, 0, 1, 0, 1, 0};       //固定權值，0,1,0,1間隔加權uint8 Trends_Curvature_Weight[19] = {4, 5, 5, 6, 6, 7, 7, 8, 8, 8, 8, 8, 7, 7, 6, 6, 5, 5, 4};      //動態權值，高權值放中間uint8 Start_Line = (uint8)((float)(Y_Meet - 2) / 18.0f * 16.0f + 24.0f);    //動態權替換固定權起始行，我圖像為60行，最低從24行向上替換，最高為40行向上替換，Y_Meet最大值為20//將動態權值賦值給固定權值數組for(i = 0; i < 19; i ++){Base_Curvature_Weight[Start_Line - i] = Trends_Curvature_Weight[i];}for(i = start; i < end - 1; i++)    //求差值和并求出權值{Sum_Difference_Value += (int16)(My_ABS((int)line[i] - (int)line[i + 1]) * (int)Base_Curvature_Weight[i]);Sum_Weight += (int16)Base_Curvature_Weight[i];}if(Sum_Weight != 0)     //防止權值為0，但好像不會出現，當時不知道為啥要寫這個{Last_Curvature_Value = (float)Sum_Difference_Value / (float)Sum_Weight;     //求加權平均值，歸一化放在了另一個函數里return Last_Curvature_Value;}else{return Last_Curvature_Value;}
}

2.速度擬合

? ? ? ? 除了曲率，速度擬合還需引入爬線相遇點Y值作為第二個參考數據，下面這部分代碼思想有一定深度：

float Speed_Value[7] = {0.0f, 0.166f, 0.333f, 0.5f, 0.666f, 0.833f, 1.0f};  //速度采用了歸一化，將1.0均分為六段float Speed_Vague_Array[4][4] = { {0, 1, 2, 3},{1, 2, 3, 4},{3, 4, 5, 6},{5, 6, 6, 6}};    //映射數組int16 Y_Meet_Count = 0;     //累積滿足相遇點條件的次數，比如由彎道進入直道時，車身未轉正時Y_Meet已經趨近于2了，此時加速會導致車軌跡不穩//那我們就進行一定的緩沖，當Y_Meet滿足我們設定的條件一定次數后，再去執行相應的加速程序，可確保車身轉正再加速
/**
* 函數功能：      使用相遇點和曲率映射速度，參照模糊PID思想
* 特殊說明：      無
* 形  參：        float sensitivity                //曲率
*                 float speed_min_proportion       //速度最小比率（設定最小速度與最大速度的比值），為0~1之間
*                 float Speed_max_proportion       //速度最大比率，通常為1
*                 uint8 y_meet                     //爬線相遇點的Y坐標
*                 uint8 min_y_meet                 //爬線相遇點的最小值，看得越遠值越小
*                 uint8 max_y_meet                 //爬線相遇點的最大值，看得越遠值越大
*
* 示例：          Calculate_Curvature_2(C_Line, Y_Meet, L_Start_Point[1]);
* 返回值：        Last_Curvature_Value      所得曲率
*/
float Speed_Mapping(float sensitivity, float speed_min_proportion, float Speed_max_proportion, uint8 y_meet, uint8 min_y_meet, uint8 max_y_meet)
{uint16 i = 0;float VH = 0, VE = 0;float X2Y = 0;float X1Y = 0;float Y2X = 0;float Y1X = 0;uint8 View_Effictive_Line = max_y_meet - min_y_meet;//彎道、環島、十字時設定最大速度為35（這是我們組控制位給的一個值，換成自己組的）if(Element_State == L_Turn ||  Element_State == R_Turn || Element_State == L_Circle || Element_State == R_Circle || Element_State == Cross){Y_Meet_Count = 0;Max_Speed = 35;}//下面就是所說的緩沖代碼，彎道到直道切換時，爬線相遇點Y趨近于2，當滿足一千次以后（計算一千張圖像），將最大速度設定為40//另一方面更重要的是為了防止誤判，導致亂加減速//沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！//沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！//沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！沖！else if(Y_Meet <= 4 && Max_Speed == 35){Y_Meet_Count ++;if(Y_Meet_Count >= 1000){Y_Meet_Count = 0;Max_Speed = 40;}}//一次不滿足就重新來，比較嚴格，可以不用或者判定放緩一些else if(Y_Meet != 2 && Max_Speed == 35){Max_Speed = 35;Y_Meet_Count = 0;}//直道到彎道的緩沖（作用于彎道在圖像最遠端，還未識別到彎道時），這個緩沖時間短一些，減速快些，這兩個計數值根據自己情況調整else if(Y_Meet != 2 && Max_Speed == 40){Y_Meet_Count --;if(Y_Meet_Count <= -350){Y_Meet_Count = 0;Max_Speed = 35;}}//獲取左右兩側邊線落在邊框上的個數Get_L_Border_Point_Num();Get_R_Border_Point_Num();//當識別出元素是直道，爬線相遇點位于頂端，左右兩側幾乎沒有落在邊框上的點，并且中線曲率很小時，直接返回最大速度開沖！//此處判定十分嚴格，不會誤判，不滿足時才執行下方速度擬合部分代碼if(Element_State == 2 && Y_Meet <= 3 && L_Border_Point_Num <= 2 && R_Border_Point_Num <= 2 && sensitivity <= 0.2f){return Max_Speed;}//下面使用曲率和爬線相遇點Y坐標擬合速度//與模糊PID原理相同，不過多注釋VH = ((float)(Y_Meet - 2) * 3.0f / (float)View_Effictive_Line);VE = sensitivity * 3.0f;int8 VH1 = (int8)VH;if (VH1 > VH){VH--;}int8 VH2 = VH1 + 1;int8 VE1 = (int8)VE;if (VE1 > VE){VE1--;}int8 VE2 = VE1 + 1;if (VH1 > 3){VH1 = 3;}if (VH2 > 3){VH2 = 3;}if (VE1 > 3){VE1 = 3;}if (VE2 > 3){VE2 = 3;}X2Y = (Speed_Vague_Array[VH1][VE2] - Speed_Vague_Array[VH1][VE1]) * (VE - VE1) + Speed_Vague_Array[VH1][VE1];X1Y = (Speed_Vague_Array[VH2][VE2] - Speed_Vague_Array[VH2][VE1]) * (VE - VE1) + Speed_Vague_Array[VH2][VE1];Y2X = (Speed_Vague_Array[VH2][VE1] - Speed_Vague_Array[VH1][VE1]) * (VH - VH1) + Speed_Vague_Array[VH1][VE1];Y1X = (Speed_Vague_Array[VH2][VE2] - Speed_Vague_Array[VH1][VE2]) * (VH - VH1) + Speed_Vague_Array[VH1][VE2];float Speed_approximation = (X2Y + X1Y + Y2X + Y1X) / 4.0;int8 Speed_1 = (int8)Speed_approximation;if (Speed_1 > Speed_approximation){Speed_1--;}int8 Speed_2 = Speed_1 + 1;return (1.0f - ((Speed_Value[Speed_2] - Speed_Value[Speed_1]) * (Speed_approximation - Speed_1) + Speed_Value[Speed_1])) * (float)(Max_Speed - Min_Speed) + (float)Min_Speed;   //返回擬合好的速度
}

3.速度控制

? ? ? ? 我們需要一個整體的函數進行速度的調控，減速拉伸部分有一定難度（也可以不使用），多讀幾次就好，下面上代碼：

float Last_Sensitivity = 0;
float Temp_Sensitivity = 0;
float Speed_Proportion_Array[100] = {0};    //用于滑動均值濾波
/**
* 函數功能：      進行速度控制使用相遇點和曲率映射速度，參照模糊PID思想
* 特殊說明：      無
* 形  參：        uint8 Auto_Control_Flag           是否要車輛自行控制速度
*                                                   //當自動控制標志位為1時，速度根據中線曲率和相遇點進行擬合
*                                                   //當自動控制標志位為0時，速度由手動輸入                              
*                 uint16 Manual_Control_Value       //手動控制速度
*
* 示例：          Fitting_Speed_Control(1, 0);
* 返回值：        無
*/
void Fitting_Speed_Control(uint8 Auto_Control_Flag, uint16 Manual_Control_Value, uint8 element, uint8 element_state, uint8 start, uint8 end)
{uint8 i = 0;if(Auto_Control_Flag == 1){float Temp_Speed_Proportion = 0;//計算中線曲率，用于速度控制Last_Sensitivity = Sensitivity;Temp_Sensitivity = Calculate_Curvature_2(C_Line, Y_Meet, L_Start_Point[1]) / 1.0f;//計算最小速度比率Speed_Min_Proportion = (float)Min_Speed / (float)Max_Speed;//Stretch_Coefficient：減速拉伸系數，此參數越大，減速距離越短，最大值為1//Stretch_Coefficient 等于手動設定一個曲率最小閾值，小于這個閾值時直接將曲率設為0if(Temp_Sensitivity <= Stretch_Coefficient){Sensitivity = 0.0f;}else    //將（閾值~1.0）之間的數進行拉伸，可以代入幾個實際的數理解下這部分原理{float Temp_Float_Num = (Temp_Sensitivity - Stretch_Coefficient) * (1.0f / (1.0f - Stretch_Coefficient));Sensitivity = Limit_Float(Temp_Float_Num * 0.3f + Last_Sensitivity * 0.7f, 0.01f, 1.0f);    //曲率值濾波}Temp_Speed_Proportion = Speed_Mapping(Sensitivity, Speed_Min_Proportion, 1.0f, Y_Meet, 2, 12);  //計算速度Speed_Proportion = Limit_Float(Temp_Speed_Proportion, (float)Min_Speed, (float)Max_Speed);  //速度限幅//滑動均值濾波，防止速度突變float Speed_Proportion_Sum = 0;for(i = 0; i < 99; i ++){Speed_Proportion_Array[i + 1] = Speed_Proportion_Array[i];}Speed_Proportion_Array[0] = Speed_Proportion;for(i = 0; i < 100; i ++){Speed_Proportion_Sum += Speed_Proportion_Array[i];}Speed_Proportion = Speed_Proportion_Sum / 100.0f;}    else{//手動控制速度部分的代碼相必就很簡單了，我這里比較亂，需讀者自行編寫了}
}