Mamba模型

為什么要提出mamba模型？

transformer特點：訓練快，推理慢，計算成本O（n*n）

Rnn的特點：訓練慢，推理快，容易遺忘

其實很容易理解，因為RNN的輸入只包含前一個隱藏層和當前的輸入，而transformer需要考慮之前所有（或者加窗）的TOKENS

transformer模型的優勢在于，它能夠回溯并利用序列中任何早期tokens的信息，以此來生成每個tokens的表征。Transformer模型由兩部分核心結構組成：一是用于理解文本內容的編碼器模塊，二是用于生成文本輸出的解碼器模塊。這兩種結構通常聯合使用，以應對包括機器翻譯在內的多種語言處理任務。

我們可以利用這種結構，僅通過解碼器來構建生成模型。
基于Transformer的這種模型，被稱為Generative Pre-trained Transformer（GPT），它使用解碼器模塊來處理并續寫給定的文本輸入。例如給定一個句子前半部分，讓模型預測下一個單詞是什么。

狀態空間模型（SSM）

狀態空間模型(State Space Model,SSM) 與 Transformer 和 RNN 一樣，用于處理信息序列，例如文本和信號

1. 什么是狀態空間？
狀態空間是一組能夠完整捕捉系統行為的最少變量集合。它是一種數學建模方法，通過定義系統的所有可能狀態來表述問題。

讓我們用一個更簡單的例子來理解這個概念。想象我們正在走過一個迷宮。這里的“狀態空間”就像是迷宮中所有可能位置的集合，即一張地圖。地圖上的每個點都代表迷宮中的一個特定位置，并包含了該位置的詳細信息，比如離出口有多遠。

而“狀態空間表示”則是對這張地圖的抽象描述。它告訴我們當前所處的位置（當前狀態）、我們可以移動到哪些位置（未來可能的狀態），以及如何從當前位置轉移到下一個狀態（比如向左轉或向右轉）

雖然狀態空間模型利用方程和矩陣來記錄這種行為，但它們本質上是一種記錄當前位置、可能的前進方向以及如何實現這些移動的方法。

描述狀態的變量（在我們的迷宮例子中，這些變量可能是X和Y坐標以及與出口的相對距離）被稱作“狀態向量”。

這個概念聽起來是不是有些耳熟？那是因為在語言模型中，我們經常使用嵌入或向量來描述輸入序列的“狀態”。例如，當前位置的向量（即狀態向量）可能如下所示：

在神經網絡的語境中，“狀態”通常指的是網絡的隱藏狀態。在大型語言模型的背景下，隱藏狀態是生成新tokens的一個關鍵要素。

2. 什么是狀態空間模型？

狀態空間模型（SSM）是用來描述這些狀態表示，并根據給定的輸入預測下一個可能狀態的模型。

在傳統意義上，SSM在時間 t 的工作方式如下：

將輸入序列 x ( t ) 例如，迷宮中的左移和下移，可以理解為之前時刻的移動軌跡）映射到潛在的狀態表示 h ( t )（例如，距離出口的遠近以及X/Y坐標）。
然后從這個狀態表示中推導出預測的輸出序列 y ( t ) （例如，為了更快到達出口而再次左移，即下一個時刻的動作）。

核心方程

狀態方程展示了輸入如何影響狀態（通過矩陣B），以及狀態如何隨時間變化（通過矩陣A）。

輸出方程描述了狀態如何轉換為輸出（通過矩陣 C）?以及?輸入如何影響輸出（通過矩陣 D ）

狀態空間模型具體流程

可視化這兩個方程為我們提供了以下架構：

1、設想我們有一個輸入信號 x ( t ) x(t)x(t)，這個信號首先與矩陣B相乘，而矩陣B刻畫了輸入對系統的影響程度。

2.我們將這個狀態與矩陣A相乘，矩陣A揭示了所有內部狀態是如何相互連接的，因為它們代表了系統的基本動態。?矩陣A在創建狀態表示之前被應用，并在狀態表示更新之后進行更新。

接著，我們利用矩陣C來定義狀態如何轉換為輸出。

3、最后，我們可以利用矩陣D提供從輸入到輸出的直接信號。這通常也稱為跳躍連接，類似于殘差連接。

這兩個方程共同作用，目的是根據觀測數據來預測系統的狀態。由于輸入被假定為連續的，狀態空間模型的主要表現形式是連續時間表示。

3. 從連續信號到離散信號

對于連續信號，直接找到狀態表示 h ( t ) h(t)h(t) 在分析上可能頗具挑戰。此外，由于我們通常處理的都是離散輸入（比如文本序列），我們希望將模型轉換為離散形式。

Zero-Order Hold Technoloty

為了實現這一點，我們采用了零階保持（Zero-Order Hold, ZOH）技術。其工作原理如下：每當接收到一個離散信號時，我們就保持該信號值不變，直到下一個離散信號的到來。這個過程實際上創建了一個SSM可以處理的連續信號。

我們保持信號值的時間由一個新的可學習參數表示，這個參數稱為步長 Δ。它代表了輸入信號的分辨率。

現在，由于我們有了連續的輸入信號，我們能夠生成連續的輸出信號，并且只需根據輸入信號的時間步長來對輸出值進行采樣。這些采樣值構成了我們的離散輸出。

數學表示

從數學角度來看，我們可以按照以下方式應用零階保持技術：

關于運用ZOH零階保持法把連續SSM轉換為離散SSM的詳細推導這里不再贅述，感興趣的讀者可以自行查閱資料。

因此，可以將連續狀態空間模型（SSM）轉換為離散形式，其公式不再是連續函數到函數的映射

x ( t ) → y ( t )，而是離散序列到序列的映射 $x_{k}\rightarrow y_{k}$

????????這里，矩陣A和B現在表示模型的離散參數。使用 k kk 而不是 t tt 來表示離散時間步長，并在提到連續 SSM 與離散 SSM 時使其更加清晰。

????????在訓練期間仍然保存矩陣 A的連續形式，而不是離散化版本。在訓練過程中，連續表示被離散化。

現在我們已經有了離散表示的公式，讓我們探索如何實際計算模型。

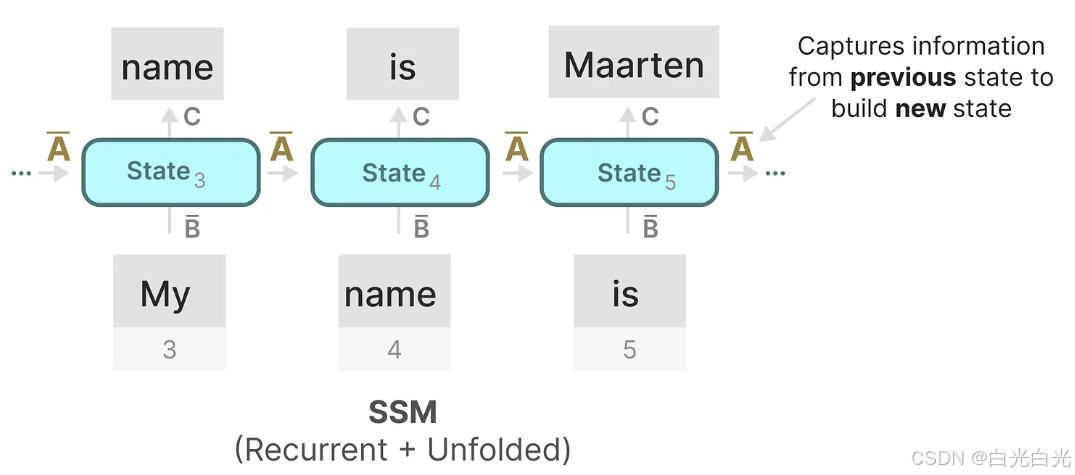
4. 循環表示

離散 SSM 允許我們以特定的時間步長而不是連續信號來表述問題。正如我們之前在 RNN 中看到的那樣，循環方法在這里非常有用。如果我們考慮離散時間步長而不是連續信號，我們可以用時間步長重新表述問題：

5. 卷積表示

另一種可用于狀態空間模型（SSM）的表示形式是卷積。
在傳統的圖像識別任務中，使用?濾波器(或稱卷積核)?提取圖像的聚合特征：

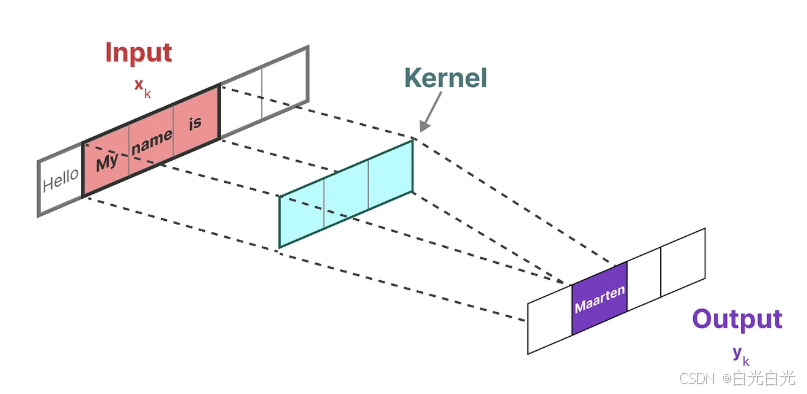
我們用來表示這種“濾波器”的內核是從SSM模型推導而來的：

這可以被轉換為一個具有明確的核公式的單個卷積操作：

6. 三種表示

這三種表示法，連續的，循環的，和卷積的都有不同的優點和缺點：

有趣的是，我們現在可以在推理時利用循環SSM的高效性，并在訓練時利用卷積SSM的并行處理能力。

借助這些不同的表示形式，我們可以采用一種巧妙的方法，即根據不同的任務需求選擇合適的表示。在訓練階段，我們采用可以并行計算的卷積表示，以便加快訓練速度；而在推理階段，我們則切換到高效的循環表示，以優化推理性能：(給我的啟示，既然可以把連續的做成離散的，并且在不同的階段利用TRANSFORMER訓練快的優勢，而RNN推理快的優勢，量子版本也是如此)