文章目錄
- 從結構到操作:手撕AVL樹的實現
- 一、AVL樹介紹
- 1.1 什么是AVL樹
- 1.2 平衡因子的定義
- 1.3 平衡的意義
- 1.4 AVL樹的操作
- 二、AVL樹的節點結構
- 2.1 節點結構的定義:
- 三、插入操作
- 3.1 插入操作概述
- 3.2 步驟1:按二叉查找樹規則插入節點
- 3.3 步驟2:更新平衡因子
- 3.4 步驟3:旋轉操作詳解
- 3.4.1 右單旋
- 3.4.2 左單旋
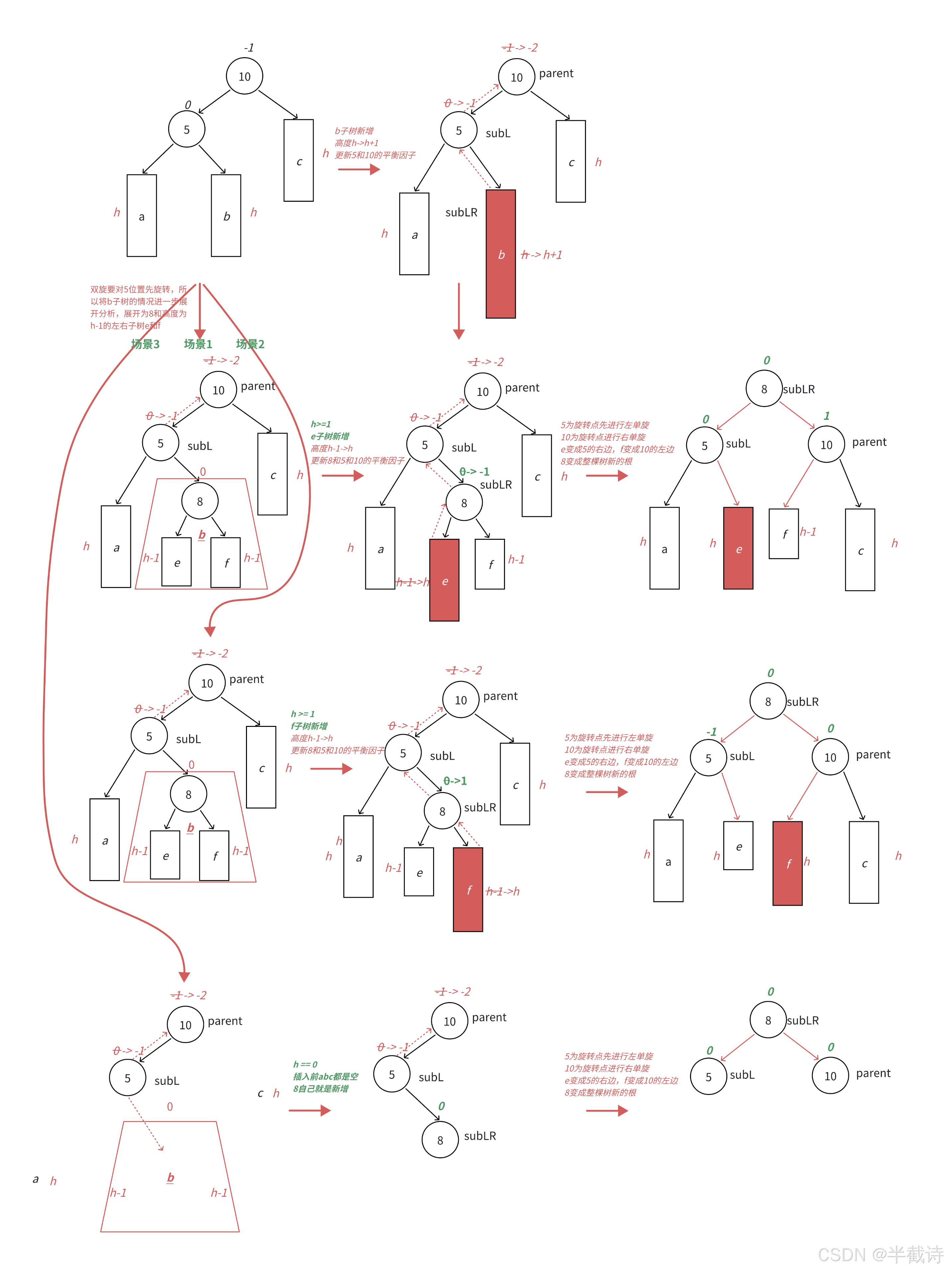
- 3.4.3 左右雙旋
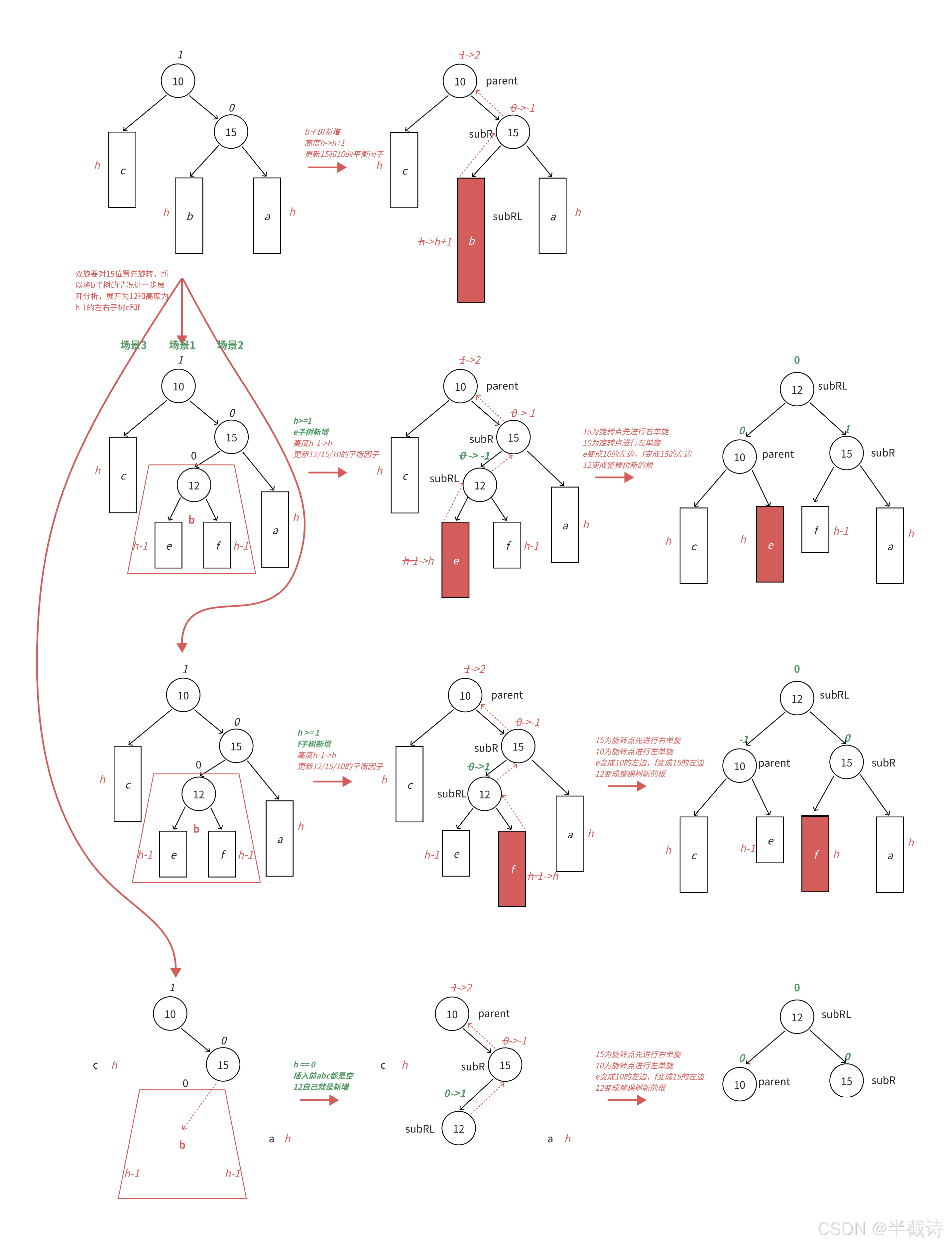
- 3.4.4 右左雙旋
- 四、其他操作
- 4.1 查找操作 (`Find`)
- 4.2 計算樹的高度 (`Height`)
- 4.3 計算節點數量 (`Size`)
- 4.4 樹是否平衡 (`IsBalanceTree`)
- 五、性能分析與測試
- 5.1 性能分析
- 5.2 測試代碼
- 六、全部代碼
- 七、總結與展望
從結構到操作:手撕AVL樹的實現
💬 歡迎討論:如果你在閱讀過程中有任何疑問或想要進一步探討的內容,歡迎在評論區留言!我們一起學習、一起成長。
👍 點贊、收藏與分享:如果你覺得這篇文章對你有幫助,記得點贊、收藏并分享給更多的朋友!
🚀 逐步實現AVL樹:本篇文章將帶你一步一步實現一個自平衡的二叉查找樹——AVL樹,從最基本的節點結構開始,逐步實現插入、查找等操作,并確保每個步驟都詳細講解。
一、AVL樹介紹
1.1 什么是AVL樹
AVL樹是一種自平衡的二叉查找樹(BST),由G.M. Adelson-Velsky和E.M. Landis于1962年提出。AVL樹的核心特點是它保證樹的每個節點的左右子樹的高度差(平衡因子)不超過1,從而保證了AVL樹在插入、刪除和查找操作時的時間復雜度始終為O(log N)。
1.2 平衡因子的定義
每個節點都有一個平衡因子(_bf),它表示節點左子樹的高度減去右子樹的高度:
平衡因子 = 左子樹的高度 ? 右子樹的高度 \text{平衡因子} = \text{左子樹的高度} - \text{右子樹的高度} 平衡因子=左子樹的高度?右子樹的高度
- 如果平衡因子為 0,表示左右子樹的高度相等。
- 如果平衡因子為 1,表示左子樹比右子樹高1。
- 如果平衡因子為 -1,表示右子樹比左子樹高1。
1.3 平衡的意義
AVL樹的自平衡特性確保了其查詢、插入和刪除操作的最壞時間復雜度為O(log N),避免了普通二叉查找樹的退化(比如變成鏈表)。因此,AVL樹非常適用于需要頻繁插入和刪除操作的場景。
1.4 AVL樹的操作
AVL樹的主要操作有:
- 插入操作:在樹中插入節點,并在插入后調整平衡因子。如果平衡因子為2或-2,執行旋轉操作恢復平衡。
- 刪除操作:刪除節點,并且在刪除節點后,可能需要調整樹的結構以保持平衡。由于AVL樹的刪除操作涉及復雜的旋轉和調整,因此在本文中我們不會詳細講解該操作。如果你希望深入了解,可以參考《算法導論》中的相關章節來獲取詳細內容。
- 查找操作:通過比較節點值來查找特定的元素。
- 旋轉操作:當樹失衡時,使用旋轉來恢復平衡,常見的旋轉有左旋、右旋、左右旋和右左旋。
二、AVL樹的節點結構
在實現AVL樹之前,首先要定義節點結構。每個節點存儲以下信息:
- 鍵值對(
_kv):存儲數據(pair<K, V>)。 - 左右子樹指針(
_left,_right):指向左右子樹。 - 父節點指針(
_parent):指向父節點。 - 平衡因子(
_bf):用于標識該節點的左右子樹的高度差。
2.1 節點結構的定義:
template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv; // 存儲鍵值對AVLTreeNode<K, V>* _left; // 左子樹指針AVLTreeNode<K, V>* _right; // 右子樹指針AVLTreeNode<K, V>* _parent; // 父節點指針int _bf; // 平衡因子// 構造函數AVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};
三、插入操作
3.1 插入操作概述
AVL樹的插入操作包括三步:
- 按二叉查找樹規則插入節點;
- 更新每個節點的平衡因子;
- 如果需要,進行旋轉操作來恢復樹的平衡。
bool Insert(const pair<K, V>& kv);
3.2 步驟1:按二叉查找樹規則插入節點
在插入節點時,我們根據值的大小,遞歸地找到插入位置,并在該位置插入新節點:
if (_root == nullptr) {_root = new Node(kv); // 如果樹為空,直接插入根節點return true;
}Node* parent = nullptr;
Node* cur = _root;
while (cur) {if (cur->_kv.first < kv.first) {parent = cur;cur = cur->_right; // 在右子樹中查找插入位置} else if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left; // 在左子樹中查找插入位置} else {return false; // 如果節點已存在,不插入}
}cur = new Node(kv);
if (parent->_kv.first < kv.first)
{parent->_right = cur;
}
else
{parent->_left = cur;
}
//更新插入節點的_parent
cur->_parent = parent;
3.3 步驟2:更新平衡因子
插入節點后,我們從新插入的節點開始,逐步更新路徑上每個節點的平衡因子。插入時會對父節點的平衡因子進行調整:
while (parent)
{if (cur == parent->_left){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋轉if (parent->_bf == 2 && cur->_bf == 1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateLR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateRL(parent);}elseassert(false);break;}else{assert(false);}
}
return true;
3.4 步驟3:旋轉操作詳解
如果某個節點的平衡因子為2或-2,表示該節點不平衡。我們需要通過旋轉操作來恢復平衡。旋轉操作有四種:
- 右單旋(RotateR)
- 左單旋(RotateL)
- 左右雙旋(RotateLR)
- 右左雙旋(RotateRL)
3.4.1 右單旋
右單旋適用于當左子樹較高時,執行旋轉操作來恢復平衡。


void RotateR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;Node* ppNode = parent->_parent;parent->_left = subLR;if (subLR) {subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;if (parent == _root) {subL->_parent = nullptr;_root = subL;} else {subL->_parent = ppNode;if (parent == ppNode->_right)ppNode->_right = subL;elseppNode->_left = subL;}parent->_bf = 0;subL->_bf = 0;
}
3.4.2 左單旋
左單旋適用于當右子樹較高時,執行旋轉操作來恢復平衡。


void RotateL(Node* parent) {Node* subR = parent->_right;Node* ppNode = parent->_parent;Node* subRL = subR->_left;parent->_right = subRL;parent->_parent = subR;if (subRL) {subRL->_parent = parent;}subR->_left = parent;if (parent == _root) {_root = subR;subR->_parent = nullptr;} else {subR->_parent = ppNode;if (parent == ppNode->_right)ppNode->_right = subR;elseppNode->_left = subR;}parent->_bf = 0;subR->_bf = 0;
}
3.4.3 左右雙旋


當左子樹的右子樹較高時,首先進行左旋,再進行右旋,恢復平衡。
void RotateLR(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL); // 左旋RotateR(parent); // 右旋if (bf == 1) {subLR->_bf = 0;subL->_bf = 0;parent->_bf = -1;} else if (bf == -1) {subLR->_bf = 0;subL->_bf = 1;parent->_bf = 0;} else if (bf == 0) {subL->_bf = subLR->_bf = parent->_bf = 0;}
}
3.4.4 右左雙旋
當右子樹的左子樹較高時,首先進行右旋,再進行左旋,恢復平衡。


void RotateRL(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR); // 右旋RotateL(parent); // 左旋if (bf == 0) {parent->_bf = subR->_bf = subRL->_bf = 0;} else if (bf == 1) {subRL->_bf = 0;parent->_bf = 0;subR->_bf = -1;} else if (bf == -1) {subRL->_bf = 0;parent->_bf = 1;subR->_bf = 0;}
}
總結:找失衡原因,決定如何旋轉
- 左子樹的左子樹高:進行R
- 右子樹的右子樹高:進行L
- 左子樹的右子樹高:進行LR
- 右子樹的左子樹高:進行RL
四、其他操作
4.1 查找操作 (Find)
查找操作與普通的二叉查找樹類似。通過不斷比較當前節點的鍵值和目標值,沿樹的路徑查找目標節點。
Node* Find(const K& key) {Node* cur = _root;while (cur) {if (cur->_kv.first < key)cur = cur->_right; // 目標鍵值比當前節點大,往右子樹查找else if (cur->_kv.first > key)cur = cur->_left; // 目標鍵值比當前節點小,往左子樹查找elsereturn cur; // 找到目標節點,返回該節點}return nullptr; // 如果沒有找到,返回空
}
該方法的時間復雜度為 O(log N),因為AVL樹是平衡的,樹的高度是對數級別的。
4.2 計算樹的高度 (Height)
樹的高度指的是從根節點到最遠葉子節點的最長路徑上的邊數。AVL樹的高度是平衡的,計算時我們需要遞歸地計算左右子樹的高度并返回較大的一個。
int Height() {return _Height(_root); // 從根節點開始計算樹的高度
}int _Height(Node* root) {if (root == nullptr)return 0; // 空樹的高度為0int leftHeight = _Height(root->_left); // 遞歸計算左子樹的高度int rightHeight = _Height(root->_right); // 遞歸計算右子樹的高度return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1; // 返回較大值,并加1
}
該方法的時間復雜度為 O(N),其中N為節點總數。雖然AVL樹是平衡的,但在計算高度時需要遍歷整個樹。
4.3 計算節點數量 (Size)
節點數量是樹中所有節點的總數。通過遞歸遍歷樹,計算左右子樹的節點數量,并加上當前節點。
int Size() {return _Size(_root); // 從根節點開始計算樹的大小
}int _Size(Node* root) {if (root == nullptr)return 0; // 空樹節點數量為0return _Size(root->_left) + _Size(root->_right) + 1; // 左右子樹的節點數量加1
}
該方法的時間復雜度為 O(N),需要遍歷整個樹來計算節點總數。
4.4 樹是否平衡 (IsBalanceTree)
為了驗證AVL樹的平衡性,我們需要檢查每個節點的平衡因子,并確保它們的絕對值不超過1。如果樹的任意節點的平衡因子大于1或小于-1,那么樹就不平衡。
bool _IsBalanceTree(Node* root) {if (root == nullptr)return true; // 空樹是平衡的int leftHeight = _Height(root->_left); // 左子樹高度int rightHeight = _Height(root->_right); // 右子樹高度int diff = leftHeight - rightHeight; // 計算平衡因子if (abs(diff) >= 2) {cout << root->_kv.first << "高度差異常" << endl;return false; // 如果高度差大于等于2,樹不平衡}if (root->_bf != diff) {cout << root->_kv.first << "平衡因子異常" << endl;return false; // 如果平衡因子與實際高度差不符,樹不平衡}// 遞歸檢查左右子樹是否平衡return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
該方法的時間復雜度為 O(N),需要遞歸遍歷整個樹并計算每個節點的平衡因子。
五、性能分析與測試
5.1 性能分析
AVL樹通過保持平衡,保證了插入、查找和刪除操作的時間復雜度都為O(logN),相比于普通的二叉查找樹,AVL樹避免了退化成鏈表的情況,極大提高了性能。
5.2 測試代碼
下面是兩個測試代碼,用于驗證AVL樹的插入和查找操作。
// 測試代碼
void TestAVLTree1()
{AVLTree<int, int> t;// 常規的測試用例//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的帶有雙旋場景的測試用例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });cout << "Insert:" << e << "->";cout << t.IsBalanceTree() << endl;}t.InOrder();cout << t.IsBalanceTree() << endl;
}// 插入一堆隨機值,測試平衡,順便測試一下高度和性能等
void TestAVLTree2()
{const int N = 1000000;vector<int> v;v.reserve(N);srand((unsigned int)time(0));for (int i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << t.IsBalanceTree() << endl;cout << "Insert:" << end2 - begin2 << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值/*for (auto e : v){t.Find(e);}*/// 隨機值for (int i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}
六、全部代碼
AVLTree.h
#pragma oncetemplate<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent){if (cur == parent->_left){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋轉if (parent->_bf == 2 && cur->_bf == 1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateLR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateRL(parent);}elseassert(false);break;}else{assert(false);}}return true;}void InOrder(){_InOrder(_root);}bool IsBalanceTree(){return _IsBalanceTree(_root);}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key)cur = cur->_right;else if (cur->_kv.first > key)cur = cur->_left;elsereturn cur;}return nullptr;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}private:int _Size(Node* root){if (root == nullptr)return 0;return _Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool _IsBalanceTree(Node* root){if (root == nullptr)return true;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = leftHeight - rightHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度差異常" << endl;return false;}if (root->_bf != diff) {cout << root->_kv.first << "平衡因子異常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << " ";_InOrder(root->_right);}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* ppNode = parent->_parent;parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;if (parent == _root){subL->_parent = nullptr;_root = subL;}else{subL->_parent = ppNode;if (parent == ppNode->_right)ppNode->_right = subL;elseppNode->_left = subL;}parent->_bf = 0;subL->_bf = 0;}void RotateL(Node* parent){Node* subR = parent->_right;Node* ppNode = parent->_parent;Node* subRL = subR->_left;parent->_right = subRL;parent->_parent = subR;if (subRL){subRL->_parent = parent;}subR->_left = parent;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{subR->_parent = ppNode;if (parent == ppNode->_right)ppNode->_right = subR;elseppNode->_left = subR;}parent->_bf = 0;subR->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subLR->_bf = 0;subL->_bf = 1;parent->_bf = 0;}else if (bf == 0){subL->_bf = subLR->_bf = parent->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == 1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = -1;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 1;subR->_bf = 0;}else{assert(false);}}Node* _root = nullptr;
};// 測試代碼
void TestAVLTree1()
{AVLTree<int, int> t;// 常規的測試用例//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的帶有雙旋場景的測試用例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){/*if (e == 14){int x = 0;}*/t.Insert({ e, e });cout << "Insert:" << e << "->";cout << t.IsBalanceTree() << endl;}t.InOrder();cout << t.IsBalanceTree() << endl;
}// 插入一堆隨機值,測試平衡,順便測試一下高度和性能等
void TestAVLTree2()
{const int N = 1000000;vector<int> v;v.reserve(N);srand((unsigned int)time(0));for (int i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << t.IsBalanceTree() << endl;cout << "Insert:" << end2 - begin2 << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值/*for (auto e : v){t.Find(e);}*/// 隨機值for (int i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}
Test.cpp
#define _CRT_SECURE_NO_WARNINGS 1#include<iostream>
#include<assert.h>
#include<vector>
using namespace std;
#include"AVLTree.h"int main()
{TestAVLTree1();TestAVLTree2();return 0;
}
七、總結與展望
隨著數據量的不斷增長,如何保持高效的查找與插入操作成為了現代計算機科學的核心問題之一。AVL樹作為一種自平衡二叉查找樹,憑借其穩定的時間復雜度和高效的性能,已廣泛應用于各類需要動態數據結構支持的場景。未來,隨著算法和硬件的進一步發展,AVL樹的實現和優化將迎來更多挑戰與機遇。我們期待看到更高效的樹形結構和操作算法,不斷推動計算機科學的前沿發展,同時也期待你在實現這些算法時能夠繼續探索與創新,為我們帶來更多啟發和思考。
以上就是關于【C++篇】樹影搖曳,旋轉無聲:探尋AVL樹的平衡之道的內容啦,各位大佬有什么問題歡迎在評論區指正,或者私信我也是可以的啦,您的支持是我創作的最大動力!??


)
——279. 完全平方數)


)
)


![[網絡] 如何開機自動配置靜態IP,并自動啟動程序](http://pic.xiahunao.cn/[網絡] 如何開機自動配置靜態IP,并自動啟動程序)









現代C++的關鍵性概念: 學習新算法: std::unique_copy](http://pic.xiahunao.cn/[原創](Modern C++)現代C++的關鍵性概念: 學習新算法: std::unique_copy)