前言
隨著能源問題日益突出,風力發電等以可再生能源為基礎的發電技術越來越受到關注。建立能夠正確反映實際風速特性的風速模型是研究風力發電系統控制策略以及并網運行特性的重要基礎叫。由于風速的隨機性和波動性,系統中的機械設備和電氣設備以及電網均會受到擾動,這種擾動對于系統設備的壽命、運行性能以及電網的穩定性都將產生一定的影響。因而,在研究風電場接入電網的功率波動與電能質量等動態特性時,需要建立與之相適應的風速模型。
ARMA模型
自回歸滑動平均模型(Auto-Regressive and Moving Average ,ARMA)是研究時間序列的重要方法,已廣泛應用于經濟學、股票、期貨等領域當中。其原理是利用已知的信號序列、誤差以及已知序列對信號自身的影響規律來預測未來的信號序列。ARMA模型描述了離散隨機信號中各序列之間的依存關系。ARMA模型具有以下特征:
1)以線性差分方程描述離散隨機信號序列;
2)任何一個有理式的功率譜都可以用一個ARMA隨機過程的功率密度譜精確逼近;
3)ARMA模型滿足Yule-Walker方程;
兩參數Weibull分布
兩參數的Weibull分布模型是適用范圍最廣、擬合實際風速最好的模型,它能調整參數來適應不同時間長度(通常是一個月或一年)的風速序列。在風速和風能評估方面已有很多應用。
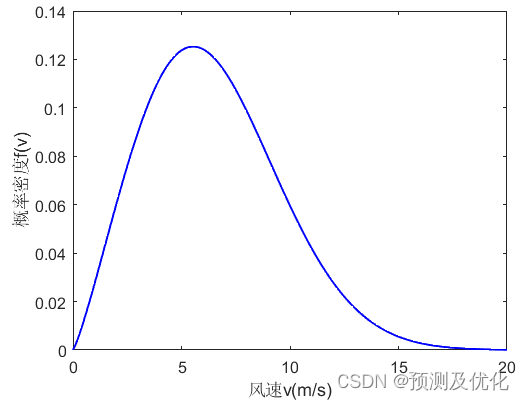
兩參數的Weibull分布的概率密度函數如下式所示:
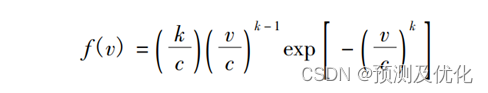
其分布函數如下式所示:
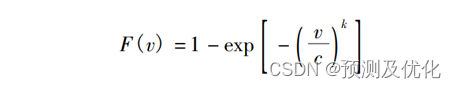
程序介紹
自回歸滑動平均模型(ARMA)是分析時間序列的重要方法。在分析實際風速統計特性和ARMA模型性質的基礎上,建立了可用于動態仿真的短期風速模型。程序結果表明,所得風速序列能夠正確反映實際風速的特性。在風能領域Weibul分布常用于描述風速的分布特征,通過擬合Weibull分布可以得到風速的概率密度分布,為風能資源的評估和風電場的布局提供重要依據。程序中算例豐富,注釋清晰,干貨滿滿,創新性和可擴展性很高,下面對程序做簡要介紹!
程序結果
ARMA模型結果
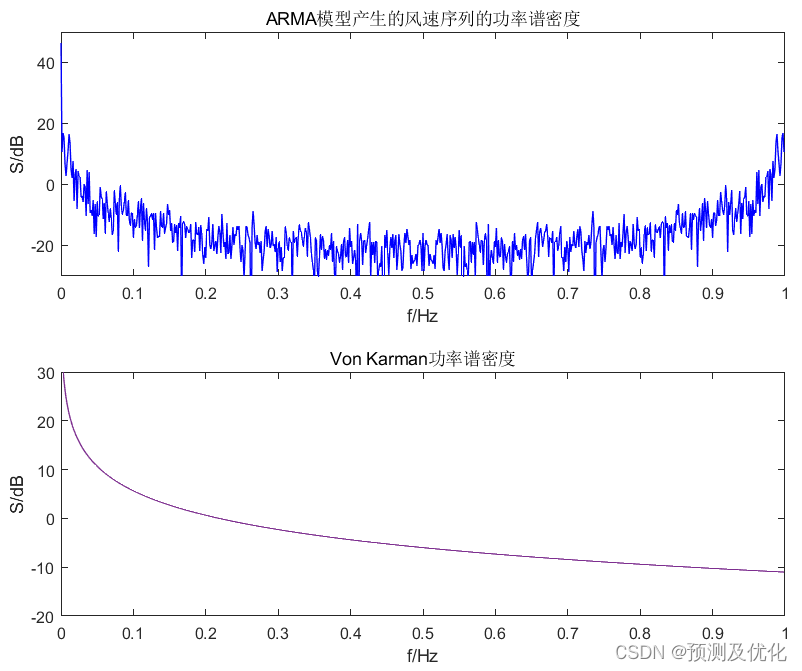
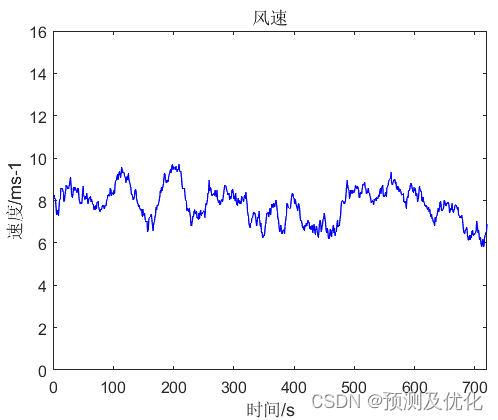
風速Weibull分布結果
部分程序
%初始化
I=0.16;%湍流強度?L=600;%湍流尺度
average_v=8.11850232757234;%平均風速
Ts=1;%采樣時間T=720;%模擬時間?n=T/Ts;%采樣個數
sigma_u=3.48648820169842;%風速序列的標準差
sigma_noise=0.2;%白噪聲的方差
% u=yyx_noice_n(0,sigma_noise,n);%產生n個序列的白噪聲,均值為0,方差為1;
u=normrnd(0,sigma_noise,n);?df=1/T;%頻率分辨率
f=(0:n-1)*df;length_f=length(f);?
?S(i)=4*(sigma_u)^2*L/average_v/(1+70.8*(f(i)*L/average_v)^2)^(5/6);%Von Karman譜功率密度函數
R=real(ifft(S));%自相關與功率譜密度是傅立葉變換關系,求自相關?
%求解AR模型參數
a(1)=R(2)/R(1);?a(2)=R(3)/R(1)-R(2)*R(2)/R(1)/R(1);
%求解MA模型參數
Ry=(-a(1)+a(2)*a(1))*R(1)+(1+a(1)^2+a(2)^2)*R(2)+(-a(1)+a(1)*a(2))*R(3)+(-a(2))*R(4);
b=Ry/sigma_noise;%beta=Ry/白噪聲的方差?
%脈動風速
v(1)=u(1);?v(2)=a(1)*v(1)+u(2)+b*u(1);
??v(k)=a(1)*v(k-1)+a(2)*v(k-2)+u(k)+b*u(k-1);%ARMA模型部分內容源自網絡,侵權聯系刪除!
歡迎感興趣的關注并私信獲取完整版代碼,小編會不定期更新高質量的學習資料、文章和程序代碼,為您的科研加油助力!














)
)
)


