這次主要講了堆排序和堆的基本構造，下一期會詳細講述堆的各種基本操作。

---

前言

這次主要講了堆排序和堆的基本構造，下一期會詳細講述堆的各種基本操作。

---

提示：以下是本篇文章正文內容，下面案例可供參考

一、堆排序

1.題目描述

輸入一個長度為?n?的整數數列，從小到大輸出前?m小的數。

輸入格式

第一行包含整數?n?和?m。

第二行包含?n?個整數，表示整數數列。

輸出格式

共一行，包含?m?個整數，表示整數數列中前?m?小的數。

數據范圍

1≤m≤n≤100000，
1≤數列中元素≤1000000000

2.堆

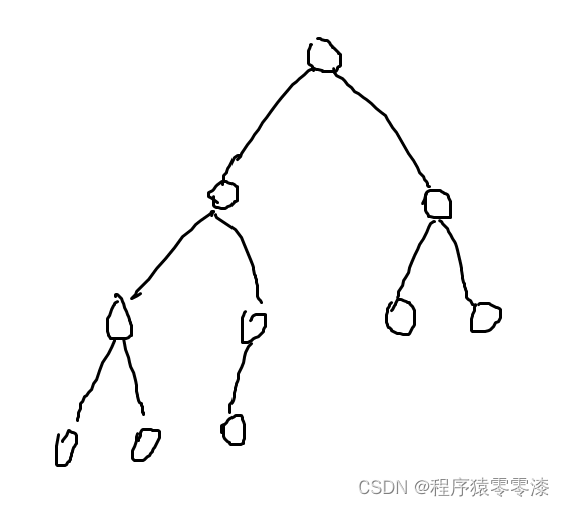
圖2.1完全二叉樹示意圖?

完全二叉樹：一棵深度為k的有n個結點的二叉樹，對樹中的結點按從上至下、從左到右的順序進行編號，每一層最多有個結點，除了最后一層，其余層的結點數都是滿的，且最后一層從左往右依次分布。

堆是一種基于完全二叉樹的數據結構。可以分為大根堆，小根堆。

大根堆：每個結點的值都大于或者等于其左右孩子的值。

小根堆：每個結點的值都小于或者等于其左右孩子的值。?

二、算法思路

1.堆的存儲

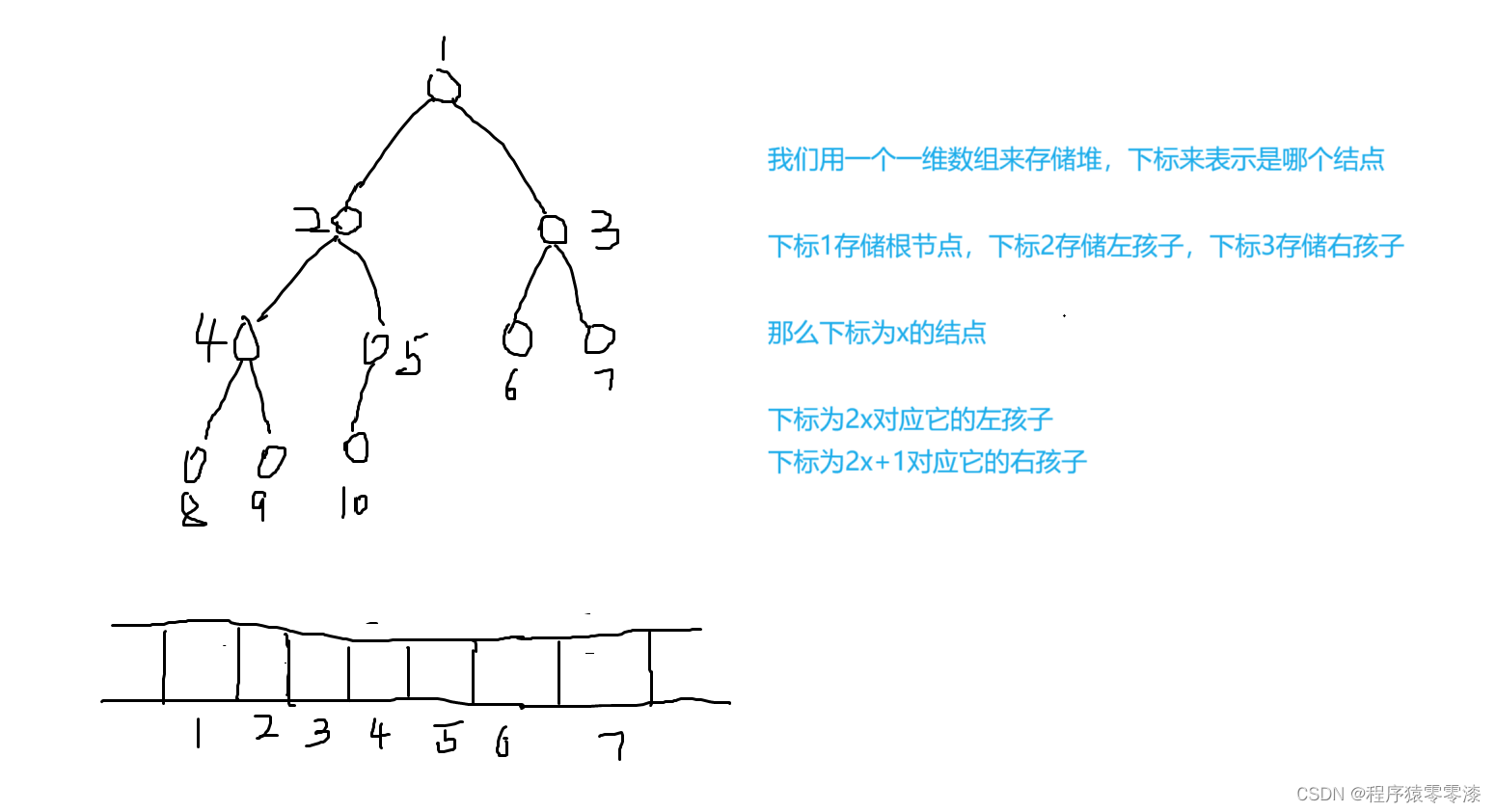
?圖1.1堆的存儲示例圖

我們用一個一維數組來存儲堆的值，下標來表示是哪個結點，下標為1就存儲根節點的值，下標為2存儲它的左孩子的值，下標為3存儲它的右孩子的值，我們就可以類比推理出任一結點的左孩子和右孩子的下標。例如下標為x的結點，它的左孩子在數組中存儲的下標就是2x，它的右孩子在數組中存儲的下標是2x+1。（注：下標從1開始）

2. 結點下移down

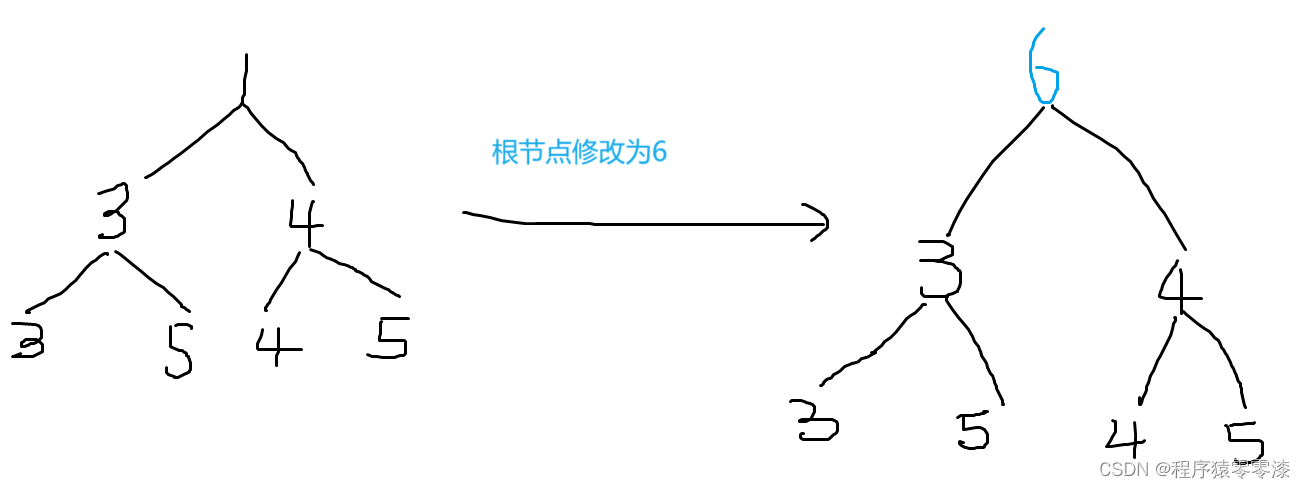
?圖2.1示例一

?我們以一個小根堆為例，父結點的值要小于它的左右孩子結點。當我們將根節點修改為6后，此時小根堆的性質就被破壞了，那么我們就要對這個小根堆進行調整。

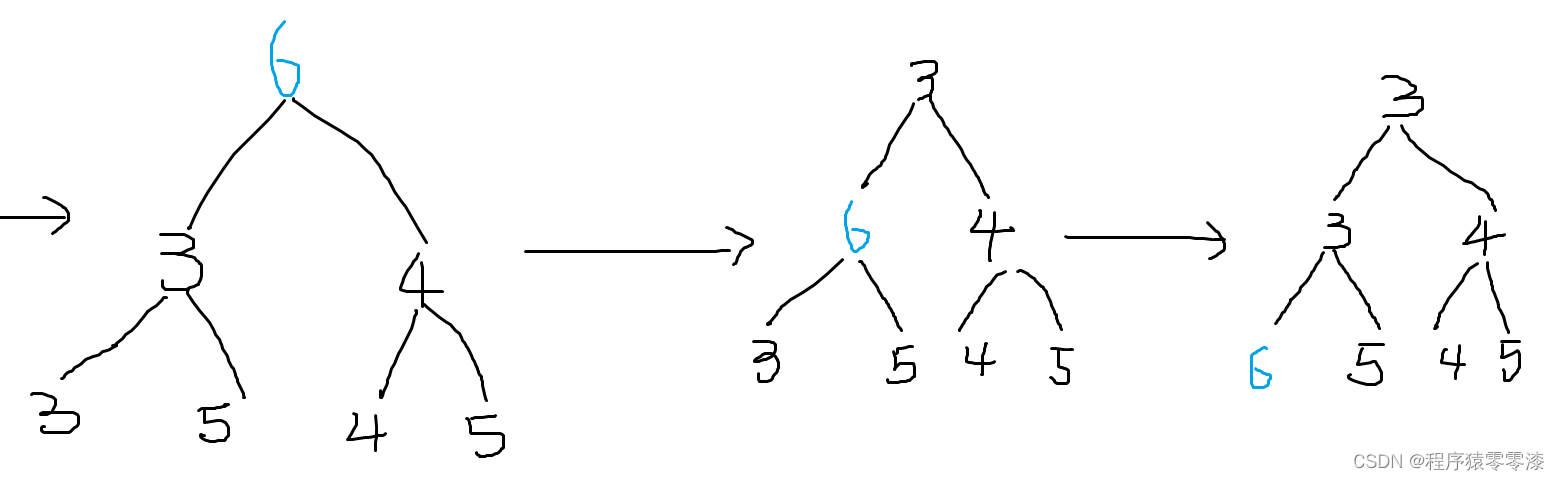
圖2.2示例二?

此時，我們需要與根節點的左右孩子進行比較，得出6的左孩子3是3個點中最小的，進行交換。此時小根堆的性質還沒維護好，此時我們還需要將6跟它的左右孩子進行比較，得出它的左孩子3是最小的，再將6和它的左孩子進行交換，此時檢查后發現，符合小根堆的性質。即我們將某一個值變大，那么在小根堆中它就要下移。

    //傳入結點下標public static void down(int x){int temp = x;//兩個if語句來找出3個結點中最小的結點的下標if(2 * x <= size && heap[2* x] < heap[temp]){temp = 2 * x;}if (2 * x + 1 <= size && heap[2*x + 1] < heap[temp]){temp = 2 * x + 1;}//說明此時結點不是最小值，進行交換，再遞歸處理看是否還需要交換if(temp != x){int t = heap[temp];heap[temp] = heap[x];heap[x] = t;down(temp);}}

3.結點上移up

?

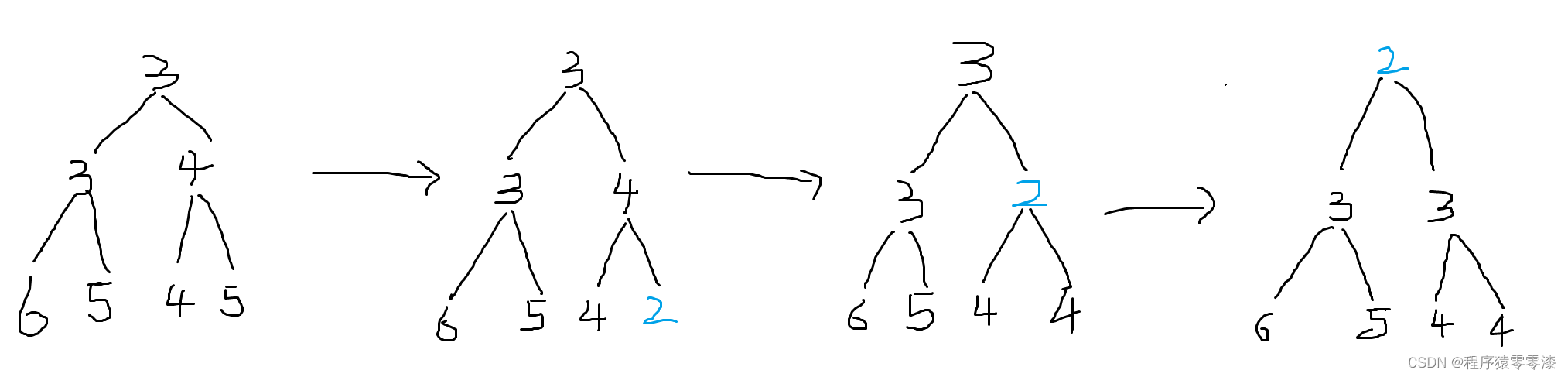
圖3.1結點上移示例?

當我們把最右下角的結點值修改為2，此時小根堆的性質被破壞。我們把2和它的父結點進行比較得出2就是3個結點的最小值，2跟它的父結點進行交換；然后。此時的2再跟它的父結點進行比較得出2是3個結點中的最小值，將2跟它的父結點進行交換。此時檢查后，發現符合小根堆的性質。可以看出如果值變大的話，我們需要進行結點上移操作，即結點上移來維護小根堆的性質。

up操作我們只需要跟父親結點比就可以了。

    //傳入結點下標public static void up(int x){int t = x;int temp =  x / 2;if(temp >= 1 && heap[temp] > heap[t]){t = temp;}if(t != x){int arr = heap[t];heap[t] = heap[x];heap[x] = arr;up(t);}}

?

4.堆的基本操作

我們引入一個一維整型數組heap來存儲堆，一個整型變量size來表示堆中最后一個元素的下標或者堆中的元素個數。（數組下標0不用，我們從下標為1開始存儲）

向堆中插入一個數：我們則直接在數組最后一個元素后面加入一個值，最后一個元素的下標為size即head[++size] = x;此時我們要預防堆的性質是否被破壞，那么我們直接執行結點上移操作即可。up(size)；

求堆中的最小值：小根堆中的根節點就是堆中的最小值即head[1]。

刪除最小值：即我們將根節點刪除了，在一維數組中第一個元素我們很難刪除，但是最后一個元素很容易刪除，我們只需要用最后一個元素將根節點覆蓋，然后將堆的大小減1即head[1] = head[size]；dowx(1)來讓結點下移來維護堆的性質。

刪除任意一個元素：刪除下標為k的結點值，我們還是用堆中的最后一個元素將這個元素值進行覆蓋，然后將堆的大小減1即head[k] = head[size]；size--；如果結點值變大的進行結點下移，結點值變小進行結點下移，那么我們直接down(k)；up(k)；因為它最后只會執行這兩個操作中的一個，這樣小根堆的性質也會被維護。

修改任意一個元素：修改下標為k的元素為x，那么我們需要head[k] = x；如果結點值變大的進行結點下移，結點值變小進行結點下移，那么我們直接down(k)；up(k)；因為它最后只會執行這兩個操作中的一個，這樣小根堆的性質也會被維護。

5.堆的初始化

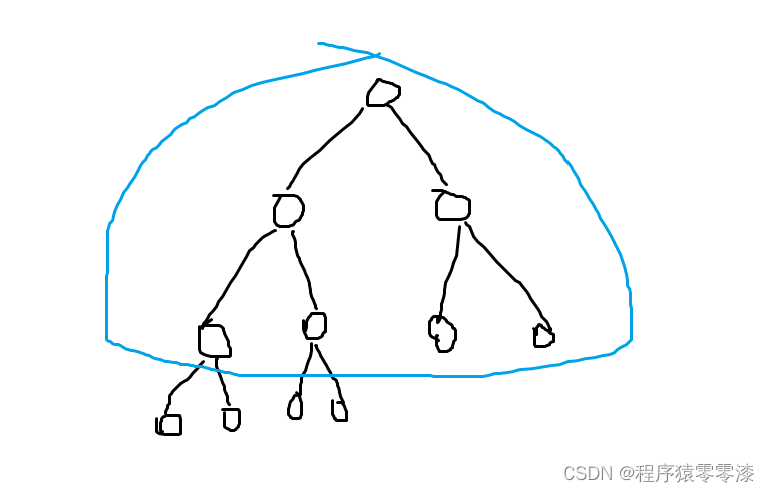
圖5.1示例圖?

因為我們需要初始化建造一個小根堆，那么我們只需要從倒數第2層開始每一個結點進行結點下移操作就可以了。最后一層是葉子節點不需要進行結點下移操作。

        for(int i = 1; i <= n; i++){heap[i] = sc.nextInt();}size = n;//初始化建堆for(int i = n / 2;i > 0;i--){down(i);}

三、代碼如下

1.代碼如下：

import java.io.*;
import java.util.*;
public class 堆排序 {static PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static int N = 100010;//存儲堆static int[] heap = new int[N];//堆中最后一個結點的下標，也是堆中元素的個數static int size = 0;public static void main(String[] args) throws Exception{Scanner sc = new Scanner(br);int n = sc.nextInt();int m = sc.nextInt();for(int i = 1; i <= n; i++){heap[i] = sc.nextInt();}size = n;//初始化建堆for(int i = n / 2;i > 0;i--){down(i);}while (m-- > 0){//打印最小值pw.print(heap[1] +" ");//刪除堆中的根節點，然后維護小根堆性質heap[1] = heap[size];size--;down(1);}pw.flush();}//傳入結點下標public static void down(int x){int temp = x;//兩個if語句來找出3個結點中最小的結點的下標if(2 * x <= size && heap[2* x] < heap[temp]){temp = 2 * x;}if (2 * x + 1 <= size && heap[2*x + 1] < heap[temp]){temp = 2 * x + 1;}//說明此時結點不是最小值，進行交換，再遞歸處理看是否還需要交換if(temp != x){int t = heap[temp];heap[temp] = heap[x];heap[x] = t;down(temp);}}//傳入結點下標public static void up(int x){int t = x;int temp =  x / 2;if(temp >= 1 && heap[temp] > heap[t]){t = temp;}if(t != x){int arr = heap[t];heap[t] = heap[x];heap[x] = arr;up(t);}}
}

2.讀入數據：

5 3
4 5 1 3 2

3.代碼運行結果

1 2 3 

---

總結

上述通過一些堆的基本操作來完成堆排序，后續會專門再寫一次博客來詳細介紹模擬堆的各種操作。